hihoCoder 1066-无间道之并查集 #1066 : 无间道之并查集 时间限制:20000ms 单点时限:1000ms 内存限制:256MB 描述 这天天气晴朗、阳光明媚、鸟语花香，空气中弥漫着春天的气息……额，说远了，总之，小Hi和小Ho决定趁着这朗朗春光出去玩。 但是刚刚离开居住的宾馆不久，抄近道不小心走入了一条偏僻小道的小Hi和小Ho就发现自己的前方走来了几个彪形大汉，定睛一看还都是地地道道的黑人兄弟！小Hi和小Ho这下就慌了神，捡肥皂事小，这一身百把来斤别一不小心葬身他乡可就没处说去了。 就在两人正举足无措之时，为首的黑叔叔从怀里掏出了一件东西——两张花花绿绿的纸，分别递给了小Hi和小Ho。 小Hi和小Ho接过来，只见上面写道（译为中文）：“本地最大的帮派——青龙帮，诚邀您的加入！”下面还详细的列出了加入青龙帮的种种好处。 于是两人略感心安，在同黑叔叔们交谈一番之后，已是均感相见恨晚。同时，在小Hi和小Ho表示自己不日便将回国之后，黑叔叔们也没有再提加入帮派之事，但是那为首的黑叔叔思索一会，开口道（译为中文）：“我现在有一个难题，思索了很久也没法子解决，既然你们俩都是高材生，不如来帮我看看。” 小Hi和小Ho点了点头表示没问题，于是黑叔叔继续说道：“这个问题是这样的，我们帮派最近混进了许多警察的卧底，但是在我们的调查过程中只能够知道诸如‘某人和另一个人是同阵营的’这样的信息，虽然没有办法知道他们具体是哪个阵营的，但是这样的信息也是很重要的，因为我们经常会想要知道某两个人究竟是不是同一阵营的。” 小Hi和小Ho赞同的点了点头，毕竟无间道也都是他们看过的。 黑叔叔接着说道：“于是现在问题就来了，我希望你们能写出这样一个程序，我会有两种操作，一种是告诉它哪两个人是同一阵营的，而另一种是询问某两个人是不是同一阵营的……既然你们就要回国了，不如现在就去我们帮派的总部写好这个程序再走把。” 为了生命安全与……小Hi和小Ho都不得不解决这个问题！那么他们究竟从何下手呢？ 提示：说起来其实就是不断的合并集合嘛~ 输入 每个测试点（输入文件）有且仅有一组测试数据。 每组测试数据的第1行为一个整数N，表示黑叔叔总共进行的操作次数。 每组测试数据的第2~N+1行，每行分别描述黑叔叔的一次操作，其中第i+1行为一个整数op_i和两个由大小写字母组成的字符串Name1_i, Name2_i，其中op_i只可能为0或1，当op_i=0时，表示黑叔叔判定Name1_i和Name2_i是同一阵营的，当op_i=1时，表示黑叔叔希望知道Name1_i和Name2_i是否为同一阵营的。 对于100%的数据，满足N<=10^5, 且数据中所有涉及的人物中不存在两个名字相同的人（即姓名唯一的确定了一个人），对于所有的i，满足Name1_i和Name2_i是不同的两个人。 输出 对于每组测试数据，对于黑叔叔每次op_i=1的操作，输出一行，表示查询的结果：如果根据已知信息（即这次操作之前的所有op_i=0的操作），可以判定询问中的两个人是同一阵营的，则输出yes，否则输出no。 样例输入 10 0 Steven David 0 Lcch Dzx 1 Lcch Dzx 1 David Dzx 0 Lcch David 0 Frank Dzx 1 Steven Dzx 1 Frank David 0 Steven Dzx 0 Dzx Frank 样例输出 yes no yes yes
这是一道考察并查集的好题目。并查集也叫做不相交集。它主要有两个操作：FIND和UNION。 假设有两个不相交集分别为A,B，用各自集合内的元素a和b分别代表A和B，也就是说A中所有元素（包括a自己）的祖先都是a，B中所有元素（包括b自己）的祖先都是b。FIND操作就是给定一个元素c，要找到它的祖先。常规思路就是递归的顺着族谱往上找，但是为了后续查找的高效，可以路径压缩一下，也就是把查找过程中的节点的祖先都赋为c的祖先，这样下次查找其他元素的祖先时就快得多。 UNION操作就是已知元素c和d，要把这两个元素所在的集合合并起来，自然就是先用FIND找到c和d的祖先，然后把其中一个祖先当做另一个祖先的祖先，这样就把两个集合合并起来了。 至于这道题，题目中的提示已经把并查集的FIND函数写出来了。
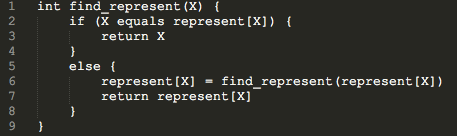如果op_i=0，说明这两个人是同一个集合的，即他们有共同的祖先，则首先判断这两个人在不在map中，如果不在，则以自身为祖先加入到map中，然后执行UNION操作把他们合并为一个集合。
如果op_i=1，要判断两个人是否在一个集合中，想当然的FIND他们的祖先，如果祖先相同，说明他们是一个集合的。
理清了上述关系，马上写出代码：
[cpp]
#include<iostream>
#include<string>
#include<map>
using namespace std;
map<string,string> represent;
//并查集FIND操作
string find_represent(string name)
{
if(name==represent[name])
return name;
else
{
represent[name]=find_represent(represent[name]);//把经过的节点全部链接到根节点
return represent[name];
}
}
int main()
{
//freopen("input.txt","r",stdin);
int n;
int op;
string name1,name2;
cin>>n;
while(n–)
{
cin>>op>>name1>>name2;
if(op==0)
{
if(represent.find(name1)==represent.end())
represent[name1]=name1;
if(represent.find(name2)==represent.end())
represent[name2]=name2;
represent[find_represent(name1)]=find_represent(name2);//UNION操作
}
else
{
//**********也需要先判断是否在map里*********
if(represent.find(name1)==represent.end())
represent[name1]=name1;
if(represent.find(name2)==represent.end())
represent[name2]=name2;
//******************************************
if(find_represent(name1)==find_represent(name2))
cout<<"yes"<<endl;
else
cout<<"no"<<endl;
}
}
return 0;
}
[/cpp]
本代码提交AC，用时243MS，内存1MB。
需要注意的是，由于本题使用MAP实现，在执行FIND操作时有这么一句：
[cpp]
if(name==represent[name])
[/cpp]
对于STL的map，如果本来map中不存在a这个元素，执行了if(map[a]==”sth”)之后，也会自动把a加入map，最后就是map[a]=””，为空。虽然就某一次来说，这样判断的结果和下面修正的结果是一样的，但是如果下一次op_i=0需要加入a时发现map中已经有a了，就直接执行UNION操作了，但是这个时候a的祖先却是空””，而本来a的祖先应该是它自己a的。所以这就会对后面的结果产生影响。所以当我们op_i=1时，如果某个人不在map中，我们也要把它加入map并使其祖先为自身。
关于这道题，这篇题解写得还可以，它把并查集的UNION和FIND分开来写，条理清晰，值得参考，不过它没有路径压缩。
之前一直对并查集心存恐惧，刷过这道题之后，发现并查集也就这么回事，代码简洁，也不难理解。继续坚持！]]>