hihoCoder 1070-RMQ问题再临 #1070 : RMQ问题再临 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 终于，小Hi和小Ho踏上了回国的旅程。在飞机上，望着采购来的特产——小Hi陷入了沉思：还记得在上上周他们去超市的时候，前前后后挑了那么多的东西，都幸运的没有任何其他人（售货员/其他顾客）来打搅他们的采购过程。但是如果发生了这样的事情，他们的采购又会变得如何呢？ 于是小Hi便向小Ho提出了这个问题：假设整个货架上从左到右摆放了N种商品，并且依次标号为1到N，每次小Hi都给出一段区间[L, R]，小Ho要做的是选出标号在这个区间内的所有商品重量最轻的一种，并且告诉小Hi这个商品的重量。但是在这个过程中，可能会因为其他人的各种行为，对某些位置上的商品的重量产生改变（如更换了其他种类的商品），面对这样一个问题，小Ho又该如何解决呢？ 提示：平衡乃和谐之理 输入 每个测试点（输入文件）有且仅有一组测试数据。 每组测试数据的第1行为一个整数N，意义如前文所述。 每组测试数据的第2行为N个整数，分别描述每种商品的重量，其中第i个整数表示标号为i的商品的重量weight_i。 每组测试数据的第3行为一个整数Q，表示小Hi总共询问的次数与商品的重量被更改的次数之和。 每组测试数据的第N+4~N+Q+3行，每行分别描述一次操作，每行的开头均为一个属于0或1的数字，分别表示该行描述一个询问和描述一次商品的重量的更改两种情况。对于第N+i+3行，如果该行描述一个询问，则接下来为两个整数Li, Ri，表示小Hi询问的一个区间[Li, Ri]；如果该行描述一次商品的重量的更改，则接下来为两个整数Pi，Wi，表示位置编号为Pi的商品的重量变更为Wi 对于100%的数据，满足N<=10^4，Q<=10^4, 1<=Li<=Ri<=N，1<=Pi<=N, 0<weight_i, Wi<=10^4。 输出 对于每组测试数据，对于每个小Hi的询问，按照在输入中出现的顺序，各输出一行，表示查询的结果：标号在区间[Li, Ri]中的所有商品中重量最轻的商品的重量。 样例输入 10 618 5122 1923 8934 2518 6024 5406 1020 8291 2647 6 0 3 6 1 2 2009 0 2 2 0 2 10 1 1 5284 0 2 5 样例输出 1923 2009 1020 1923

---

本题的数据量比hihoCoder Problem 1068: RMQ-ST 算法这题要小，虽然

用O(N)的时间进行计算——扫描一遍整个区间找到最小值，然后对于每一个更改操作，使用O(1)的时间直接进行修改，这样也就是O(NQ)的总时间复杂度！在这种数据量下完全是可以通过的！

但是本题希望我们用线段树来解决。 我曾在《数据结构》的改造红黑树中看到过区间树，但是本题的线段树和书中的区间树有所区别，区间树由红黑树改造而来，结构更复杂些，这里只需要使用线段树即可。 常规的线段树如下图所示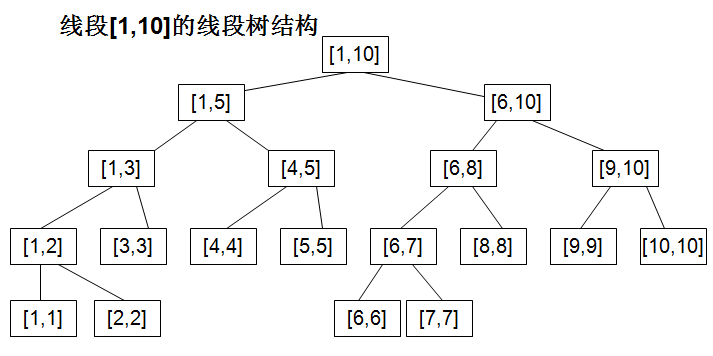： 从图中可以看到构造线段树的过程就是一个二分的过程，不断将区间分成两半，直到只有一个元素。图中的线段树每一个节点是一个区间[l,r]，本题我稍微改造了一下，改成了数组int seg_tree[left][length]，比如seg_tree[i][j]表示从下标i开始，长度为j的这样一个区间上的最小值，这样就可以利用线段树来解决RMQ问题了。比如改造后的线段树就成了下面的样子： 因为树形这种特殊的结构，我们可以用一个DFS来对树实现二分构造，当DFS到某个节点长度为1时，其最小值就是w[i]本身，在回溯到父节点时，父节那个区间的最小值又是所有子节点最小值中的最小值。因为树的总节点数大约为2*n，所以复杂度O(n)。 当需要查询区间[l,r]的最小值时，只需对数组seg_tree二分搜索。具体来说，假设我们搜索到了节点[s_l,s_len]，如果r<(s_l+s_len/2)，说明区间[l,r]全在[s_l,s_len]的左边，我们递归在[s_l,s_len/2]区间找；如果l>=(s_l+s_len/2)，说明区间[l,r]全在[s_l,s_len]的右边，我们递归在[s_l+s_len/2,s_len-s_len/2]区间找；如果以上两者都不是，说明[l,r]跨界了，而且中点下标一定是s_l+s_len/2，所以我们分别在二两半区间找，然后求这两者的最小值。复杂度O(lgn)。 当需要更新某个下标为pos的值为value时，也是DFS查找线段树，直到找到叶子seg_tree[pos][1]，更新它的值，以及所有我们在查找过程经过的父节点的值。复杂度O(lgn)。 所以线段是的性质使得无论是构造、查询、更新操作，复杂度都只要O(lgn)，这就是题目中所说的把总的复杂度平均分配到不同操作：平衡乃和谐之理。 完整代码如下： [cpp] #include<iostream> using namespace std; const int MAX_N=1e4+2; int w[MAX_N];//每个商品重量 int n,m; int seg_tree[MAX_N][MAX_N];//seg_tree[i][j]：起点为i，长度为j的区间的最小值 inline int get_min(int a,int b) { return a<b?a:b; } //深度优先遍历以构造线段树 void dfs(int left,int length) { if(length==1) { seg_tree[left][1]=w[left]; return; } dfs(left,length/2); dfs(left+length/2,length-length/2); seg_tree[left][length]=get_min(seg_tree[left][length/2],seg_tree[left+length/2][length-length/2]);//取最小值 } //在区间[s_left,s_len]搜索区间[left,length]的最小值 int search_min(int s_left,int s_len,int left,int length) { if((s_left==left)&&(s_len==length)) return seg_tree[s_left][s_len]; if((left+length-1)<(s_left+s_len/2))//全在左半部分 { return search_min(s_left,s_len/2,left,length); } else if(left>=(s_left+s_len/2))//全在右半部分 { return search_min(s_left+s_len/2,s_len-s_len/2,left,length); } else//左右分开搜索 { int left_len=s_left+s_len/2-left; int right_len=length-left_len; int min_left=search_min(s_left,s_len/2,left,left_len); int min_right=search_min(s_left+s_len/2,s_len-s_len/2,s_left+s_len/2,right_len); return get_min(min_left,min_right); } } //从区间[s_left,s_len]开始更新下标pos的值为value void update(int s_left,int s_len,int pos,int value) { if((s_left==pos)&&(s_len==1)) { seg_tree[s_left][1]=value; return ; } int mid=s_left+s_len/2; if(pos<mid) update(s_left,s_len/2,pos,value); else update(mid,s_len-s_len/2,pos,value); seg_tree[s_left][s_len]=get_min(seg_tree[s_left][s_len/2],seg_tree[mid][s_len-s_len/2]);//更新父节点 } int main() { //freopen("input.txt","r",stdin); cin>>n; for(int i=1;i<=n;i++) cin>>w[i]; dfs(1,n); cin>>m; int p,l,r; for(int i=0;i<m;i++) { cin>>p>>l>>r; if(p==0)//查询 { cout<<search_min(1,n,l,r-l+1)<<endl; } else//修改 { update(1,n,l,r); } } return 0; } [/cpp] 本代码提交AC，用时151MS，内存42MB。 ]]>