hihoCoder week 52-1-连通性·一
题目1 : 连通性·一
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
还记得上次小Hi和小Ho学校被黑客攻击的事情么,那一次攻击最后造成了学校网络数据的丢失。为了避免再次出现这样的情况,学校决定对校园网络进行重新设计。
学校现在一共拥有N台服务器(编号1..N)以及M条连接,保证了任意两台服务器之间都能够通过连接直接或者间接的数据通讯。
当发生黑客攻击时,学校会立刻切断网络中的一条连接或是立刻关闭一台服务器,使得整个网络被隔离成两个独立的部分。
举个例子,对于以下的网络:
 每两个点之间至少有一条路径连通,当切断边(3,4)的时候,可以发现,整个网络被隔离为{1,2,3},{4,5,6}两个部分:
每两个点之间至少有一条路径连通,当切断边(3,4)的时候,可以发现,整个网络被隔离为{1,2,3},{4,5,6}两个部分:
 若关闭服务器3,则整个网络被隔离为{1,2},{4,5,6}两个部分:
若关闭服务器3,则整个网络被隔离为{1,2},{4,5,6}两个部分:
 小Hi和小Ho想要知道,在学校的网络中有哪些连接和哪些点被关闭后,能够使得整个网络被隔离为两个部分。
在上面的例子中,满足条件的有边(3,4),点3和点4。
提示:割边&割点
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:若干整数,用空格隔开,表示满足要求的服务器编号。从小到大排列。若没有满足要求的点,该行输出Null
第2..k行:每行2个整数,(u,v)表示满足要求的边,u<v。所有边根据u的大小排序,u小的排在前,当u相同时,v小的排在前面。若没有满足要求的边,则不输出
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3 4
3 4
小Hi和小Ho想要知道,在学校的网络中有哪些连接和哪些点被关闭后,能够使得整个网络被隔离为两个部分。
在上面的例子中,满足条件的有边(3,4),点3和点4。
提示:割边&割点
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:若干整数,用空格隔开,表示满足要求的服务器编号。从小到大排列。若没有满足要求的点,该行输出Null
第2..k行:每行2个整数,(u,v)表示满足要求的边,u<v。所有边根据u的大小排序,u小的排在前,当u相同时,v小的排在前面。若没有满足要求的边,则不输出
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3 4
3 4
本题要求一个连通图的割边和割点,使用Tarjan算法,提示已经把dfs主要代码写了,完善一下即可。
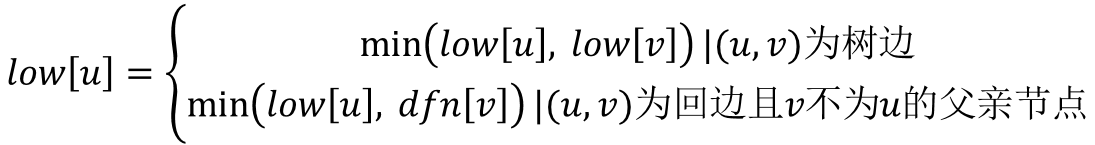 主要要理解上面的递推公式。首先理解dfn和low的含义,dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)。
上图的第一个式子,当(u,v)为树边时,low[u]表明u能追溯到的最早节点,low[v]表明u的子树(v就是u的子树的根)能追溯到的最早节点,所以根据low[u]的定义有low[u]=min(low[u],low[v])。
上图的第二个式子,当(u,v)为回边时,因为low[u]的定义就是u通过非父子边(回边)追溯最早的节点,所以既然(u,v)为回边,自然的low[u]=min(low[u],dfn[v])。
另外注意输出格式,点要从小到大排列;边(u,v)保证u<v,以u从小到大排列,再以v从小到大排列。完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<set>
#include<algorithm>
#include<vector>
using namespace std;
const int kMaxN = 20005;
int n, m;
typedef struct edge
{
int x, y;
bool operator<(const edge& p)const//如果要加入到set中,需要重载<
{
return (this->x<p.x) || ((this->x == p.x) && (this->y<p.y));
}
};
set<int> points;
set<edge> edges;
vector<vector<int>> graph;
int visit[kMaxN];
int dfn[kMaxN];
int low[kMaxN];
int parent[kMaxN];
void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;
//记录节点u的子树数
int children = 0;
visit[u] = 1;
//初始化dfn与low
dfn[u] = low[u] = ++counter;
for (int i = 0; i < graph[u].size();i++) {
int v = graph[u][i];
//节点v未被访问,则(u,v)为树边
if (visit[v]==0) {
children++;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if (parent[u] == 0 && children > 1) {
points.insert(u);
}
//case (2)
if (parent[u] != 0 && low[v] >= dfn[u]) {
points.insert(u);
}
//bridge
if (low[v] > dfn[u]) {
edge e;
e.x = u;
e.y = v;
if (u > v)
{
e.x = v;
e.y = u;
}
edges.insert(e);
}
}
//节点v已访问,则(u,v)为回边
else if (v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
scanf("%d %d", &n, &m);
graph.resize(n + 1);
int u, v;
while (m–)
{
scanf("%d %d", &u, &v);
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(1);
if (points.size() == 0)
printf("Null\n");
else
{
set<int>::iterator it = points.begin();
while (it != points.end())
{
printf("%d ", *it);
it++;
}
printf("\n");
}
if (edges.size() > 0)
{
set<edge>::iterator it = edges.begin();
while (it != edges.end())
{
printf("%d %d\n", (*it).x, (*it).y);
it++;
}
}
return 0;
}
[/cpp]
本代码提交AC,用时76MS,内存7MB。]]>
主要要理解上面的递推公式。首先理解dfn和low的含义,dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)。
上图的第一个式子,当(u,v)为树边时,low[u]表明u能追溯到的最早节点,low[v]表明u的子树(v就是u的子树的根)能追溯到的最早节点,所以根据low[u]的定义有low[u]=min(low[u],low[v])。
上图的第二个式子,当(u,v)为回边时,因为low[u]的定义就是u通过非父子边(回边)追溯最早的节点,所以既然(u,v)为回边,自然的low[u]=min(low[u],dfn[v])。
另外注意输出格式,点要从小到大排列;边(u,v)保证u<v,以u从小到大排列,再以v从小到大排列。完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<set>
#include<algorithm>
#include<vector>
using namespace std;
const int kMaxN = 20005;
int n, m;
typedef struct edge
{
int x, y;
bool operator<(const edge& p)const//如果要加入到set中,需要重载<
{
return (this->x<p.x) || ((this->x == p.x) && (this->y<p.y));
}
};
set<int> points;
set<edge> edges;
vector<vector<int>> graph;
int visit[kMaxN];
int dfn[kMaxN];
int low[kMaxN];
int parent[kMaxN];
void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;
//记录节点u的子树数
int children = 0;
visit[u] = 1;
//初始化dfn与low
dfn[u] = low[u] = ++counter;
for (int i = 0; i < graph[u].size();i++) {
int v = graph[u][i];
//节点v未被访问,则(u,v)为树边
if (visit[v]==0) {
children++;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if (parent[u] == 0 && children > 1) {
points.insert(u);
}
//case (2)
if (parent[u] != 0 && low[v] >= dfn[u]) {
points.insert(u);
}
//bridge
if (low[v] > dfn[u]) {
edge e;
e.x = u;
e.y = v;
if (u > v)
{
e.x = v;
e.y = u;
}
edges.insert(e);
}
}
//节点v已访问,则(u,v)为回边
else if (v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
scanf("%d %d", &n, &m);
graph.resize(n + 1);
int u, v;
while (m–)
{
scanf("%d %d", &u, &v);
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(1);
if (points.size() == 0)
printf("Null\n");
else
{
set<int>::iterator it = points.begin();
while (it != points.end())
{
printf("%d ", *it);
it++;
}
printf("\n");
}
if (edges.size() > 0)
{
set<edge>::iterator it = edges.begin();
while (it != edges.end())
{
printf("%d %d\n", (*it).x, (*it).y);
it++;
}
}
return 0;
}
[/cpp]
本代码提交AC,用时76MS,内存7MB。]]>