hihoCoder week 55-1-连通性·四
题目1 : 连通性·四
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi和小Ho从约翰家回到学校时，网络所的老师又找到了小Hi和小Ho。
老师告诉小Hi和小Ho：之前的分组出了点问题，当服务器(上次是连接)发生宕机的时候，在同一组的服务器有可能连接不上，所以他们希望重新进行一次分组。这一次老师希望对连接进行分组，并把一个组内的所有连接关联的服务器也视为这个组内的服务器(注意一个服务器可能属于多个组)。
这一次的条件是对于同一个组满足：当组内任意一个服务器宕机之后，不会影响组内其他服务器的连通性。在满足以上条件下，每个组内的边数量越多越好。
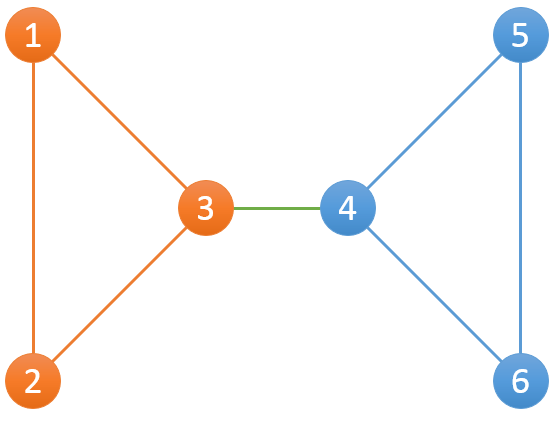
比如下面这个例子，一共有6个服务器和7条连接：
其中包含3个组，分别为{(1,2),(2,3),(3,1)},{(4,5),(5,6),(4,6)},{(3,4)}。对{(1,2),(2,3),(3,1)}而言，和该组边相关联的有{1,2,3}三个服务器：当1宕机后，仍然有2-3可以连接2和3；当2宕机后，仍然有1-3可以连接1和3；当3宕机后，仍然有1-2可以连接1和2。
老师把整个网络的情况告诉了小Hi和小Ho，希望小Hi和小Ho统计一下一共有多少个分组。
提示：点的双连通分量
输入
第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行：2个正整数，u,v。第i+1行表示存在一条边(u,v)，编号为i，连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行：1个整数，表示该网络的连接组数。
第2行：M个整数，第i个数表示第i条连接所属组内，编号最小的连接的编号。比如分为{(1,2)[1],(2,3)[3],(3,1)[2]},{(4,5)[5],(5,6)[7],(4,6)[6]},{(3,4)[4]}，方括号内表示编号，则输出{1,1,1,4,5,5,5}。
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3
1 1 1 4 5 5 5
这一题求点的双连通分量，结果是边集；上一题求了边的双连通分量，结果是点集。 点的双连通分量是指子图中去掉一个点之后还连通，求解方法还是Tarjan，和之前的题目类似。需要注意的是，提示中的伪代码有错误，有好几个地方没有将边添加到堆栈中，正确的伪代码在这里。 本题要求输出连通分量中边的最小编号，所以输入的时候要记录边的编号，并且保证当弹出堆栈时，能快速知道这是哪一条边，简单的方法是将边(u,v)映射成一个整数x，因为u,v≤20,000，所以可以令hash=max(u,v)*100000+min(u,v)。 因为点的双连通分量数等于割点数量加1，如果DFS求到有2个割点，实际有3个连通分量，所以当DFS结束时，所有没有标记的边就是最后一个连通分量。 完整代码如下： [cpp] #include<iostream> #include<cstdio> #include<vector> #include<map> #include<stack> #include<algorithm> using namespace std; const int kMaxN = 20005; const int kMaxM = 100005; map<int, int> edge_code; map<int, int> ans; vector<vector<int> > graph; vector<int> edges; stack<int> stk; bool visit[kMaxN]; int low[kMaxN]; int dfn[kMaxN]; int parent[kMaxN]; int n, m; int points=0; int HashEdge(int x, int y) { if (x > y) return x * 100000 + y; else return y * 100000 + x; } void dfs(int u) { //记录dfs遍历次序 static int counter = 0; //记录节点u的子树数 int children = 0; visit[u] = true; //初始化dfn与low dfn[u] = low[u] = ++counter; for (int i = 0; i < graph[u].size(); i++) { int v = graph[u][i]; int e = HashEdge(u, v); if (ans.find(e)!=ans.end()) continue; //节点v未被访问，则(u,v)为树边 if (!visit[v]) { children++; parent[v] = u; stk.push(e); dfs(v); low[u] = min(low[u], low[v]); //case (1) if (parent[u] == 0 && children > 1) { points++; int tmp = -1, id = kMaxM; vector<int> tmp_edges; do{ tmp = stk.top(); stk.pop(); tmp_edges.push_back(tmp); if (edge_code[tmp] < id) id = edge_code[tmp]; } while (tmp != e); for (int i = 0; i < tmp_edges.size(); i++) ans.insert(make_pair(tmp_edges[i], id)); } //case (2) if (parent[u] != 0 && low[v] >= dfn[u]) { points++; int tmp = -1, id = kMaxM; vector<int> tmp_edges; do{ tmp = stk.top(); stk.pop(); tmp_edges.push_back(tmp); if (edge_code[tmp] < id) id = edge_code[tmp]; } while (tmp != e); for (int i = 0; i < tmp_edges.size(); i++) ans.insert(make_pair(tmp_edges[i], id)); } } //节点v已访问，则(u,v)为回边 else if (v != parent[u]) { stk.push(e); low[u] = min(low[u], dfn[v]); } } } int main() { scanf("%d %d", &n, &m); graph.resize(n + 1); int u, v,tmp; for (int i = 1; i <= m; i++) { scanf("%d %d", &u, &v); graph[u].push_back(v); graph[v].push_back(u); tmp = HashEdge(u, v); edges.push_back(tmp); edge_code.insert(make_pair(tmp, i)); } dfs(1); //求解最后一个连通分量 int max_tmp = kMaxM; for (int i = 1; i <= m; i++) { if (ans.find(edges[i – 1]) == ans.end()) if (edge_code[edges[i – 1]] < max_tmp) max_tmp = edge_code[edges[i – 1]]; } printf("%dn", points + 1); for (int i = 1; i <= m; i++) printf("%d ", ans[edges[i – 1]] == 0 ? max_tmp : ans[edges[i – 1]]); return 0; } [/cpp] 本代码提交AC，用时240MS，内存10MB。]]>
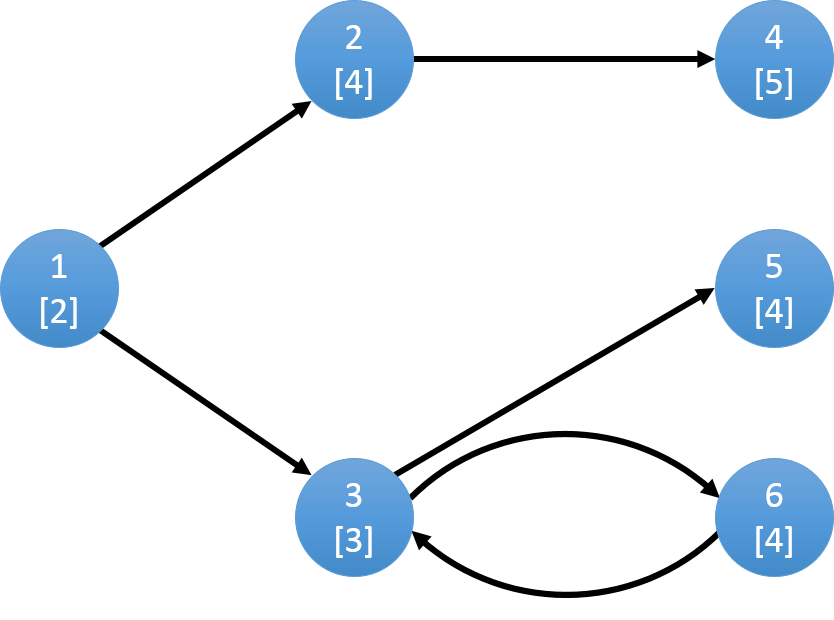图中每个点表示一个草场，上部分数字表示编号，下部分表示草场的牧草数量w。
在1吃完草之后，小Hi和小Ho可以选择把牛羊群赶到2或者3，假设小Hi和小Ho把牛羊群赶到2：
吃完草场2之后，只能到草场4，当4吃完后没有可以到达的草场，所以小Hi和小Ho就把牛羊群赶回家。
若选择从1到3，则可以到达5，6：
选择5的话，吃完之后只能直接回家。若选择6，还可以再通过6回到3，再到5。
所以该图可以选择的路线有3条：
1->2->4 total: 11
1->3->5 total: 9
1->3->6->3->5 total: 13
所以最多能够吃到的牧草数量为13。
本题改编自USACO月赛金组
提示：强连通分量
输入
第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000
第2行：N个正整数，第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000
第3..M+2行：2个正整数，u,v。表示存在一条从u到v的单向路径。1≤u,v≤N
输出
第1行：1个整数，最多能够吃到的牧草数量。
样例输入
6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3
样例输出
13
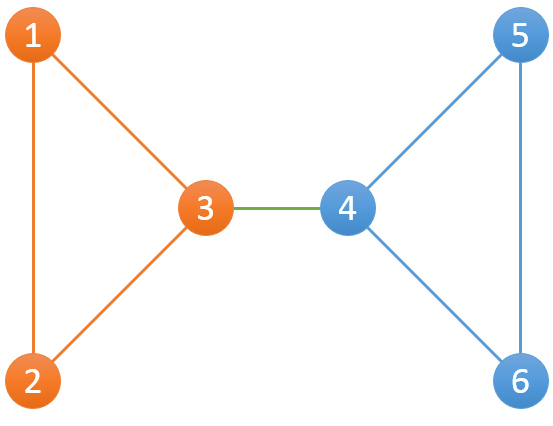
其中包含2个组，分别为{1,2,3},{4,5,6}。对{1,2,3}而言，当1-2断开后，仍然有1-3-2可以连接1和2；当2-3断开后，仍然有2-1-3可以连接2和3；当1-3断开后，仍然有1-2-3可以连接1和3。{4,5,6}这组也是一样。
老师把整个网络的情况告诉了小Hi和小Ho，小Hi和小Ho要计算出每一台服务器的分组信息。
提示：边的双连通分量
输入
第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行：2个正整数，u,v。表示存在一条边(u,v)，连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行：1个整数，表示该网络的服务器组数。
第2行：N个整数，第i个数表示第i个服务器所属组内，编号最小的服务器的编号。比如分为{1,2,3},{4,5,6}，则输出{1,1,1,4,4,4}；若分为{1,4,5},{2,3,6}则输出{1,2,2,1,1,2}
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
2
1 1 1 4 4 4
]]>
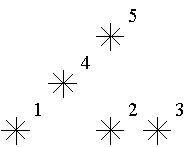For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it’s formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
You are to write a program that will count the amounts of the stars of each level on a given map.
Input
The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.
Output
The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.
Sample Input
5
1 1
5 1
7 1
3 3
5 5
Sample Output
1
2
1
1
Hint
This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.
Source
Ural Collegiate Programming Contest 1999
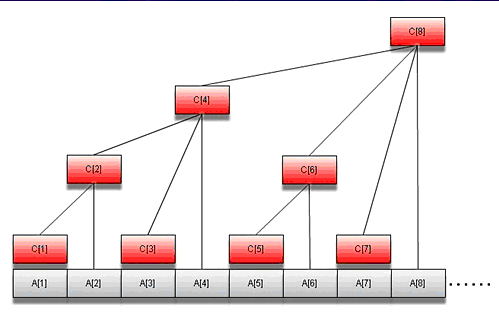树状数组[1][/caption]当来了一个横坐标为4的星星之后，其level正是A[1]+…+A[4]=C[4]，在树状数组中正好是其左下方的和。
关于树状数组可以参考[1]的文章。
所以横坐标为4的星星的level就是sum(4)。当又来了一个横坐标为4的星星之后，需要修改A[4]，使A[4]++，其实就是A[4]+1，可以使用add(4,1)操作。
因为本题中x可能等于0，但是树状数组中下标从1开始，所以需要整体将x+1。本题是树状数组的一个简单应用，完整代码如下：
[cpp]
#include<iostream>
#include<cstdio>
using namespace std;
const int kMaxN = 32005;//NOT 15005;
int n;
int level[kMaxN];
int c[kMaxN];
int lowbit(int x)
{
return x&(-x);
}
int sum(int i)
{
int rs = 0;
while (i > 0)
{
rs += c[i];
i -= lowbit(i);
}
return rs;
}
void add(int i, int val)
{
while (i <= kMaxN)
{
c[i]+=val;
i += lowbit(i);
}
}
int main()
{
scanf("%d", &n);
int x, y;
for (int i = 0; i < n; i++)
{
scanf("%d %d", &x, &y);
x++;
level[sum(x)]++;
add(x, 1);
}
for (int i = 0; i < n; i++)
printf("%dn", level[i]);
return 0;
}
[/cpp]
本代码提交AC，用时188MS，内存344K。
参考：
[1].