141. Linked List Cycle

Given a linked list, determine if it has a cycle in it.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Follow up:

Can you solve it using O(1) (i.e. constant) memory?

---

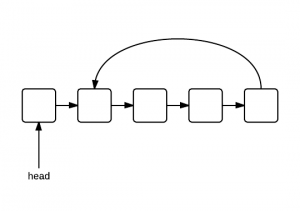
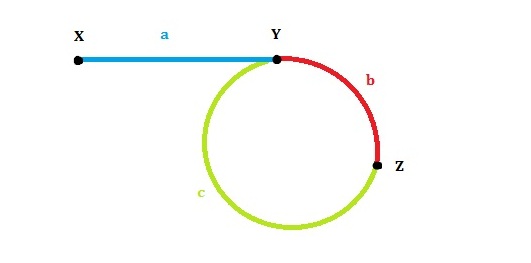
本题要判断一个链表中是否包含环，注意这里的环可能是局部的环，并不一定是链表头尾相连那种环，比如下图。 解题思路是使用快慢指针，如果链表中有环，则快慢指针一定会在某处相遇，证明请看这篇博客，我试着重述一遍： 首先请看示意图，假设链表起点为X，环的起点为Y，环的总长度为c，快慢指针在环的Z点相遇，YZ=b，XY=a。则有

a+b+mc=s—(1)

a+b+nc=2s—-(2)

(1)和(2)式分别为慢快指针的等式，其中s表示慢指针走过的节点，则快指针走过两倍的s，m和n分别为慢快指针绕圈的圈数，显然n>m。 把(1)代入(2)得到a+b=(n-2m)c。假设真的存在环，则a和c是链表的固有值，是已知量，所以如果能找到m,n,b的一组解，则说明假设成立，真的存在环。 令m=0,n=a,b=ac-a，则这一组解是满足上面的方程(1)和(2)的，也满足n>m。因为环的长度>1，所以b也是大于0的。既然找到一组解，说明假设成立，即存在环。也就是说，我们可以用这种方法判断环是否存在。 完整代码如下：

class Solution {
public:
    bool hasCycle(ListNode* head)
    {
        if (head == NULL || head->next == NULL)
            return false;
        ListNode *faster = head, *slower = head;
        while (faster->next != NULL && faster->next->next != NULL) {
            faster = faster->next->next;
            slower = slower->next;
            if (faster == slower)
                return true;
        }
        return false;
    }
};

本代码提交AC，用时9MS。
证明参考：
https://stackoverflow.com/a/6110767/2468587
https://math.stackexchange.com/a/913529/161019