hihoCoder 1040-矩形判断 #1040 : 矩形判断 时间限制:1000ms 单点时限:1000ms 内存限制:256MB 描述 给出平面上4条线段，判断这4条线段是否恰好围成一个面积大于0的矩形。 输入 输入第一行是一个整数T(1<=T<=100)，代表测试数据的数量。 每组数据包含4行，每行包含4个整数x1, y1, x2, y2 (0 <= x1, y1, x2, y2 <= 100000)；其中(x1, y1), (x2,y2)代表一条线段的两个端点。 输出 每组数据输出一行YES或者NO，表示输入的4条线段是否恰好围成矩形。 样例输入 3 0 0 0 1 1 0 1 1 0 1 1 1 1 0 0 0 0 1 2 3 1 0 3 2 3 2 2 3 1 0 0 1 0 1 1 0 1 0 2 0 2 0 1 1 1 1 0 1 样例输出 YES YES NO
这一题题意很简单，但是要写代码实现还是有很多细节需要考虑。 题目给出了4条线段的8个端点，问是否能由这4条线段构成一个面积大于0的矩形。脑海中立马浮现出一个矩形的形状。要构成一个矩形的首要条件是： 1. 有且只有4个互异的顶点 这个条件是显而易见的，如下图(1)给出的4条线段，虽然延长一下能组成矩形，但是很明显如果只由线段组成的话，不是一个矩形。
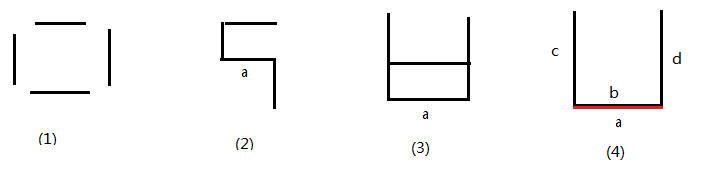要判断给出的点是否只有4个点，第一反应是用set集合，只要把题目给出的8个点都加入到set中，判断集合大小是否是4就可以了。
首先给出点的定义：
[cpp]
//点结构体
typedef struct P
{
int x,y;//两点坐标
bool operator<(const P& p)const//如果要加入到set中，需要重载<
{
//return this->x<p.x&&this->y<p.y;//注意这样会导致(0,0)<(0,1)且(0,1)<(0,0)的情况
return (this->x<p.x)||((this->x==p.x)&&(this->y<p.y));
}
bool operator==(const P&p)const//重载等于比较
{
return (this->x==p.x)&&(this->y==p.y);
}
};
[/cpp]
需要注意一点，因为需要把P加入到set中，而set是通过红黑树来排序的，所以需要重载小于<操作符。我最开始重载函数是这样写的
[cpp]
return this->x<p.x&&this->y<p.y;
[/cpp]
但是这样会有问题，如果给出两个点(0,0)和(0,1)，会得出(0,0)<(0,1)和(0,1)<(0,0)都不成立的结论，也就是说无法给(0,0)和(0,1)排序，也就无法插入到set中，所以需要修改成
[cpp]
return (this->x<p.x)||((this->x==p.x)&&(this->y<p.y));
[/cpp]
这样就能判断(0,0)<(0,1)成立了。有关这个问题可以参考这个和这个。
经过以上的步骤，就把问题转换成已知4个点，问能否由这4个点构成一个矩形的问题了。
此时又可以得出以下两个结论
2. 矩形中某条边和另外3条边的关系是：和其中2条边垂直，和另外1条边平行
3. 且和它平行的那条边不能是重合的边
有的同学可能会说，像上图中的(2)和(3)也是边a和另外2条边垂直、1条边平行啊，但是他们都不是矩形，但是大家别忘了，当我们走到这一步的时候，已经经过了第1个条件的检验，也就是只有4个顶点，你看图(2)和(3)明显不止4个顶点啊。所以结论2成立。
又有同学说，为什么还要结论3呢？因为还可能出现如上图(4)的样子，虽然图中所有边都满足条件2：和2条边垂直、和1条边平行，但是这明显不是一个矩形。因为边a和b重合了。所以结论3还是有必要的。
有了以上3条结论，我们就可以判断给出的4条线段是否能组成一个矩形了。
编程中有一些数学知识需要掌握的是，已知两个线段的4个端点，怎样判断这两条线段的关系：平行？垂直？其他？
很自然想到用斜率，如果k1*k2==-1则垂直，如果k1==k2则平行，否则其他。但是会遇到线段和y轴平行的情况，此时斜率是不存在的，所以需要稍微变一下。
假设线段L1的两个端点分别为(x1,y1)和(x2,y2)，线段L2的两个端点分别为(a1,b1)和(a2,b2)，则k1*k2==-1可以转换为(y2-y1)*(b2-b1)==-(x2-x1)*(a2-a1)。类似的，k1==k2转换为(y2-y1)*(a2-a1)==(b2-b1)*(x2-x1)。这样就不用担心斜率不存在的问题。
经过以上详细的分析，我们可以写出如下代码：
[cpp]
#include<iostream>
#include<set>
#include <vector>
using namespace std;
//点结构体
typedef struct P
{
int x,y;//两点坐标
bool operator<(const P& p)const//如果要加入到set中，需要重载<
{
//return this->x<p.x&&this->y<p.y;//注意这样会导致(0,0)<(0,1)且(0,1)<(0,0)的情况
return (this->x<p.x)||((this->x==p.x)&&(this->y<p.y));
}
bool operator==(const P&p)const//重载等于比较
{
return (this->x==p.x)&&(this->y==p.y);
}
};
//线结构体
typedef struct L
{
P p1,p2;//一条线由两点组成
};
//判断两条线的关系，1：垂直 0：平行 -1：其他
int check_two_line(L l1,L l2)
{
int x1=l1.p1.x,y1=l1.p1.y,x2=l1.p2.x,y2=l1.p2.y;
int a1=l2.p1.x,b1=l2.p1.y,a2=l2.p2.x,b2=l2.p2.y;
if((y2-y1)*(b2-b1)==-(x2-x1)*(a2-a1))//斜率公式的变形
return 1;
else if((y2-y1)*(a2-a1)==(b2-b1)*(x2-x1))
return 0;
else
return -1;
}
//判断是否是同一条直线
bool is_same_line(L l1,L l2)
{
if(((l1.p1==l2.p1)&&(l1.p2==l2.p2))||((l1.p1==l2.p2)&&(l1.p2==l2.p1)))//如果线的两个端点都相同，则是同一条直线
return true;
else
return false;
}
//判断能否组成一个矩形
bool is_rect(vector<L> lines)
{
int vertical_num,parallel_num;
for(int i=0;i<4;i++)//每条线都和剩余3条线判断关系
{
vertical_num=0;
parallel_num=0;
for(int j=0;j<4;j++)
{
if(j==i)//不和自己判断
continue;
int rs=check_two_line(lines[i],lines[j]);
if(rs==-1)
return false;
else if(rs==1)
vertical_num++;
else
{
if(is_same_line(lines[i],lines[j]))//如果是平行线还要判断是否是相同的线
return false;
parallel_num++;
}
}
if(!(vertical_num==2&¶llel_num==1))//只有当该线和其他2条线垂直，1条线平行时，才能组成矩形
return false;
}
return true;
}
int main()
{
int T;
cin>>T;
while(T–)
{
set<P> points;
vector<L> lines;
for(int i=0;i<4;i++)
{
P p1,p2;
cin>>p1.x>>p1.y>>p2.x>>p2.y;
points.insert(p1);
points.insert(p2);
L l;
l.p1=p1;
l.p2=p2;
lines.push_back(l);
}
if(points.size()!=4)//能组成矩形的必要条件是有且只有4个点，所以用set来判断更方便
cout<<"NO"<<endl;
else
{
if(is_rect(lines))
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
}
return 0;
}
[/cpp]
代码提交后AC，用时1MS，内存0MB，还不错。
]]>