POJ 1045-Bode Plot Bode Plot Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 12888 Accepted: 8184 Description Consider the AC circuit below. We will assume that the circuit is in steady-state. Thus, the voltage at nodes 1 and 2 are given by v1 = VS coswt and v2 = VRcos (wt + q ) where VS is the voltage of the source, w is the frequency (in radians per second), and t is time. VR is the magnitude of the voltage drop across the resistor, and q is its phase. 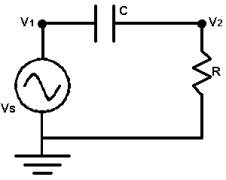 You are to write a program to determine VR for different values of w. You will need two laws of electricity to solve this problem. The first is Ohm’s Law, which states v2 = iR where i is the current in the circuit, oriented clockwise. The second is i = C d/dt (v1-v2) which relates the current to the voltage on either side of the capacitor. “d/dt”indicates the derivative with respect to t. Input The input will consist of one or more lines. The first line contains three real numbers and a non-negative integer. The real numbers are VS, R, and C, in that order. The integer, n, is the number of test cases. The following n lines of the input will have one real number per line. Each of these numbers is the angular frequency, w. Output For each angular frequency in the input you are to output its corresponding VR on a single line. Each VR value output should be rounded to three digits after the decimal point. Sample Input 1.0 1.0 1.0 9 0.01 0.031623 0.1 0.31623 1.0 3.1623 10.0 31.623 100.0 Sample Output 0.010 0.032 0.100 0.302 0.707 0.953 0.995 1.000 1.000 Source Greater New York 2001
这是一道数学+物理题，计算$$V_R$$的过程如下： 已知： ①$$v_1 = V_Scoswt$$ ②$$v_2 = V_R cos (wt+\theta )$$ ③$$v_2 = iR$$ ④$$i = C d/dt (v_1-v_2)$$ 把④代入③得⑤：$$v_2 =CR d/dt (v_1-v_2)$$ 再把①和②代入⑤得⑥：$$v_2=CR d/dt (V_Scoswt-V_R cos (wt+\theta ))$$ $$d/dt$$为对$$t$$求导，所以把⑥中的$$coswt$$和$$cos(wt+\theta )$$对$$t$$求导得到⑦：$$v_2=CRw(V_Rsin(wt+\theta )-V_Ssinwt)$$ 又因为②式，所以得到⑧：$$V_R cos (wt+\theta )=CRw(V_Rsin(wt+\theta )-V_Ssinwt)$$ 令$$wt+\theta =0$$，⑧式变为⑨：$$V_R=CRw(V_Ssin\theta)$$ 令$$t=0$$，⑧式变为⑩：$$tan\theta=1/CRw$$ 简单画一个三角形：
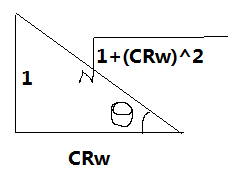快速得到$$sin\theta=1/\sqrt{1+(CRw)^2}$$，代入⑨式得到最终结果：$$V_R=CRwV_S/\sqrt{1+(CRw)^2}$$
得到了公式，快速写出代码：
[cpp]
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
int main()
{
//freopen("input.txt","r",stdin);
double vs,r,c,w,vr;
int n;
cin>>vs>>r>>c>>n;
while(n–)
{
cin>>w;
vr=c*r*w*vs/sqrt(1+c*r*w*c*r*w);
printf("%.3lf\n",vr);
}
return 0;
}
[/cpp]
本代码提交AC，用时0MS，内存208K。
]]>