POJ 1330-Nearest Common Ancestors
Nearest Common Ancestors
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 19432 Accepted: 10292
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
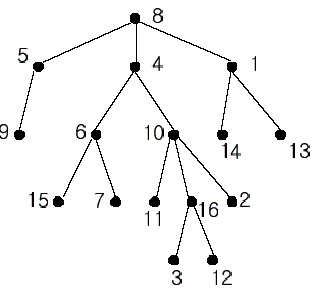In the figure, each node is labeled with an integer from {1, 2,…,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,…, N. Each of the next N -1 lines contains a pair of integers that represent an edge –the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N – 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
Source
Taejon 2002
昨天被hihoCoder Problem 1067: 最近公共祖先·二的离线算法虐了之后，今天在POJ上找了一个水题来重塑信心，这个题也是最近公共祖先问题，只不过它是目前为止最简单的，和hihoCoder Problem 1062: 最近公共祖先·一类似，甚至更简单，因为这个题每个case只询问一次，所以没必要用离线算法，而且给的就是数字，不是字符串，连转换都不要。直接记录一个节点node1的所有祖先，然后从下往上查找另一个节点node2的所有祖先，每找到一个祖先，则判断这个祖先是否是node1的祖先，如果是，则这就是他们的公共祖先。 这一次我甚至连set和map都没有用，因为给定的是连续的整数，直接用数组当hash即可，而且查找效率比set和map还快。 完整代码如下： [cpp] #include<iostream> #include<vector> using namespace std; int main() { //freopen("input.txt","r",stdin); int t,n; int node1,node2; cin>>t; while(t–) { cin>>n; vector<int> s_f(n+1,0);//s_f[i]为第i个节点的父亲，开始时所有节点的父亲为0 for(int i=0;i<n-1;i++) { cin>>node1>>node2; s_f[node2]=node1;//保存输入关系 } cin>>node1>>node2; vector<int> node1_father(n+1,0);//node1的父亲 node1_father[node1]=1;//自己是自己的祖先 while(s_f[node1]!=0) { node1_father[s_f[node1]]=1;//记录哪些点是node1的父亲 node1=s_f[node1]; } if(node1_father[node2]!=0)//node2也是自己的祖先 { cout<<node2<<endl; continue; } while(s_f[node2]!=0) { if(node1_father[s_f[node2]]!=0)//从下网上找node2的祖先是否出现在node1的祖先里 { cout<<s_f[node2]<<endl; break; } else node2=s_f[node2]; } } return 0; } [/cpp] 本代码提交AC，用时125MS，内存336K。 关于最近公共祖先问题，还有一种牛逼的在线算法RMQ，在hihoCoder上也有提到，下回再战！]]>