POJ 1163-The Triangle
The Triangle
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 38525 Accepted: 23126
Description
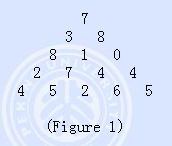Figure 1 shows a number triangle. Write a program that calculates the highest sum of numbers passed on a route that starts at the top and ends somewhere on the base. Each step can go either diagonally down to the left or diagonally down to the right.
Input
Your program is to read from standard input. The first line contains one integer N: the number of rows in the triangle. The following N lines describe the data of the triangle. The number of rows in the triangle is > 1 but <= 100. The numbers in the triangle, all integers, are between 0 and 99.
Output
Your program is to write to standard output. The highest sum is written as an integer.
Sample Input
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30
Source
IOI 1994
DP水题一个，如果将等边三角形转换成Sample Input里的等腰直角三角形，设则某一点的路径和为sum[i][j]，则因为只能从(i-1,j)和(i-1,j-1)这两个点到达(i,j)，所以sum[i][j]=max{sum[i-1][j],sum[i-1][j-1]}+triangle[i][j]。如果为了节省空间，j可以从i downto 0循环，也就是DP表从右往左填，这样只需要一行空间。 不多说，简单题，直接上代码。 [cpp] #include<iostream> using namespace std; const int MAX_N=101; int triangle[MAX_N][MAX_N]; int sum[MAX_N]={0}; int DP(int n) { int rs=0; for(int i=0;i<n;i++) { for(int j=i;j>=0;j–)//从右往左填表，只需一行空间 { if(j>0) { sum[j]=(sum[j]>sum[j-1]?sum[j]:sum[j-1])+triangle[i][j]; } else if(j==0) { sum[j]+=triangle[i][j]; } if(sum[j]>rs)//记录最大值 rs=sum[j]; } } /*int rs=0; for(int i=0;i<n;i++) if(sum[i]>rs) rs=sum[i];*/ return rs; } int main() { //freopen("input.txt","r",stdin); int n; cin>>n; for(int i=0;i<n;i++) for(int j=0;j<=i;j++) cin>>triangle[i][j]; cout<<DP(n); return 0; } [/cpp] 本代码提交AC，用时0MS,内存260K。 ]]>