hihoCoder 1050-树中的最长路 #1050 : 树中的最长路 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 上回说到，小Ho得到了一棵二叉树玩具，这个玩具是由小球和木棍连接起来的，而在拆拼它的过程中，小Ho发现他不仅仅可以拼凑成一棵二叉树！还可以拼凑成一棵多叉树——好吧，其实就是更为平常的树而已。 但是不管怎么说，小Ho喜爱的玩具又升级换代了，于是他更加爱不释手（其实说起来小球和木棍有什么好玩的是吧= =）。小Ho手中的这棵玩具树现在由N个小球和N-1根木棍拼凑而成，这N个小球都被小Ho标上了不同的数字，并且这些数字都是出于1..N的范围之内，每根木棍都连接着两个不同的小球，并且保证任意两个小球间都不存在两条不同的路径可以互相到达。总而言之，是一个相当好玩的玩具啦！ 但是小Hi瞧见小Ho这个样子，觉得他这样沉迷其中并不是一件好事，于是寻思着再找点问题让他来思考思考——不过以小Hi的水准，自然是手到擒来啦！ 于是这天食过早饭后，小Hi便对着又拿着树玩具玩的不亦乐乎的小Ho道：“你说你天天玩这个东西，我就问你一个问题，看看你可否知道？” “不好！”小Ho想都不想的拒绝了。 “那你就继续玩吧，一会回国的时候我不叫上你了~”小Hi严肃道。 “诶！别别别，你说你说，我听着呢。”一向习惯于开启跟随模式的小Ho忍不住了，马上喊道。 小Hi满意的点了点头，随即说道：“这才对嘛，我的问题很简单，就是——你这棵树中哪两个结点之间的距离最长？当然，这里的距离是指从一个结点走到另一个结点经过的木棍数。”。 “啊？”小Ho低头看了看手里的玩具树，困惑了。 提示一：路总有折点，路径也不例外！ 输入 每个测试点（输入文件）有且仅有一组测试数据。 每组测试数据的第一行为一个整数N，意义如前文所述。 每组测试数据的第2~N行，每行分别描述一根木棍，其中第i+1行为两个整数Ai，Bi，表示第i根木棍连接的两个小球的编号。 对于20%的数据，满足N<=10。 对于50%的数据，满足N<=10^3。 对于100%的数据，满足N<=10^5，1<=Ai<=N, 1<=Bi<=N 小Hi的Tip：那些用数组存储树边的记得要开两倍大小哦！ 输出 对于每组测试数据，输出一个整数Ans，表示给出的这棵树中距离最远的两个结点之间相隔的距离。 样例输入 8 1 2 1 3 1 4 4 5 3 6 6 7 7 8 样例输出 6
本题要求一棵树中相距最远两点之间的距离，也就是`树的直径`。 求树的直径有多种方法，我这里介绍两种。 第一种方法 第一种方法很好理解，我们随机的从某个节点s对树深度优先遍历（广度优先遍历也行），找到深度最大的叶子节点node1；然后再从node1点对树DFS，找到深度最大的叶子节点node2；则node1和node2即为这棵树中相距最远的两个点，它们之间的距离即为树的直径。 关于这种方法的简要证明，可以看这篇博客。 这种方法简单易懂，可以很快的写出代码，如下： [cpp] #include<iostream> #include<vector> using namespace std; const int MAX_N=1e5+2; int n;//节点数 int longest;//最远距离 int node1,node2;//node1，node2分别为为第一、二次DFS找到的最远点 vector<vector<int> > f_s(MAX_N);//father-son和son-father关系，存储双边 //参数分别为当前节点，深度，父亲节点 void dfs(int root,int depth,int father) { if(depth>longest)//更新 { longest=depth; node1=root; } int sons=f_s[root].size(); for(int i=0;i<sons;i++) { if(f_s[root][i]!=father)//不能回溯 dfs(f_s[root][i],depth+1,root); } } int main() { //freopen("input.txt","r",stdin); cin>>n; int a,b; for(int i=0;i<n-1;i++) { cin>>a>>b; f_s[a].push_back(b);//记录双边关系 f_s[b].push_back(a);//记录双边关系 } longest=0; dfs(1,0,-1);//随机选一个点（1）找到第一个最远点node1 longest=0; dfs(node1,0,-1);//以node1找第二个最远点node2，则node1到node2即为整棵树的直径 cout<<longest; return 0; } [/cpp] 本代码提交AC，用时255MS，内存9MB。 有一点需要提醒的是，因为不仅需要从s开始DFS，还需要从node1开始DFS，所以需要存储双向边，即不仅要存储(v,u)，还需要存储(u,v)；这样存了之后，为了防止DFS时回溯到父节点造成死循环，在DFS时要判断下一个节点是不是父节点，如果是则不继续DFS。 第二种方法 第一种方法虽然简单易懂，但不是hiho题目中给出的方法，那么hiho给出的又是什么方法呢？且看官方提示：
“没错，我枚举每一个点作为转折点t，求出以t为根节点的子树中的‘最长路’以及与‘最长路’不重合的‘次长路’，用这两条路的长度之和去更新答案，那么最终的答案就是这棵树的最长路长度了！”小Hi道。 “原来是这样，也就是说我只要以类似后序遍历的方式依次访问每个结点，从下往上依次计算每个结点的first值和second值，我就能够用O(N)的时间复杂度来解决这个问题咯！”这提示的第一句话我倒是理解了，但是第二句一直不懂，为什么只要O(N)就可以解决问题呢。不管了，先看看只用第一句话能否AC吧。 我一开始的理解是这样的：尝试枚举每一个点为树的根节点t，然后从t开始DFS，找到以t为根的树的最长路径和次长路径（最长和次长路径不能有重复边），然后把他们加起来就是以t为根节点的树找到最长路径，而且这条最长路径肯定经过了根节点t。 比如样例输入，分别以节点1、2、3为根构成的树如下：
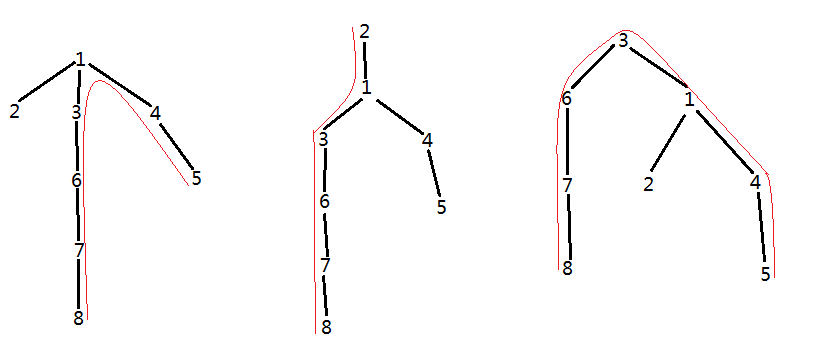因为我们默认以t为根的树的最长路径一定经过节点t，所以上图最长路径分别为图中红色路线所示，长度分别为6,5,6（因为节点1和3都在最长路径上，所以他们求得的最长路径相等）。同理我们还可以求出以4,5…n为根（路径转折点）的最长路径，最后求这些最长路径中的最大值。
这个版本的代码如下：
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int MAX_N=1e5+2;
int n;//节点数
vector<vector<int> > f_s(MAX_N);//father-son和son-father关系，存储双边
vector<int> first,second;//first[i]和second[i]分别表示以i节点为根节点时（i节点以下构成的子树）的最大和次大长度
//参数分别为当前节点，父亲节点
void dfs(int root,int father)
{
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
if(f_s[root][i]!=father)//不能回溯
{
dfs(f_s[root][i],root);
if(first[f_s[root][i]]+1>first[root])
{
second[root]=first[root];
first[root]=first[f_s[root][i]]+1;
}
else if(first[f_s[root][i]]+1>second[root])
second[root]=first[f_s[root][i]]+1;
}
}
}
void init_first_second()
{
first.clear();
first.assign(n+1,0);
second.clear();
second.assign(n+1,0);
}
int main()
{
freopen("input.txt","r",stdin);
cin>>n;
int a,b;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
f_s[a].push_back(b);//记录双边关系
f_s[b].push_back(a);//记录双边关系
}
int ans=0;
for(int i=1;i<=n;i++)//枚举每一个节点为根节点（转折点）
{
init_first_second();
dfs(i,-1);
if(first[i]+second[i]>ans)
ans=first[i]+second[i];
}
cout<<ans;
return 0;
}
[/cpp]
但是很遗憾，提交后TLE。
后来我仔细想了想，无论我们从哪个点s开始对树DFS，我们求得的first[i]和second[i]都是以点i为根构成的子树中它的最长和次长距离，那么first[i]+second[i]不就代表了从i开始DFS时得到的最长距离吗？比如图中以2为根的树中，我们在DFS的过程中肯定已经求到了first[1]和second[1]，然后才能求first[2]和second[2]，而这里的first[1]和second[2]和图中以1为根时求得的first[1]和second[1]是完全一样的。而对于以3为根的树，因为3正好在最长路径上，所以这里的first[1]和second[1]要小于前面两种情况，但是first[3]+second[3]和前面两种情况的first[1]+second[1]是相等的。
说了这么多，不知道同学们有没有发现，不管从哪个点开始DFS，只要一遍DFS结束，最长路径总会出现在某个first[i]+second[i]中。
至此，可以省略上一个版本中的for循环，只要一个DFS即可：
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int MAX_N=1e5+2;
int n;//节点数
vector<vector<int> > f_s(MAX_N);//father-son和son-father关系，存储双边
vector<int> first,second;//first[i]和second[i]分别表示以i节点为根节点时（i节点以下构成的子树）的最大和次大长度
int longest=0;//最终结果
//参数分别为当前节点，父亲节点
void dfs(int root,int father)
{
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
if(f_s[root][i]!=father)//不能回溯
{
dfs(f_s[root][i],root);
if(first[f_s[root][i]]+1>first[root])//更新最大和次大
{
second[root]=first[root];
first[root]=first[f_s[root][i]]+1;
}
else if(first[f_s[root][i]]+1>second[root])//只更新次大
second[root]=first[f_s[root][i]]+1;
}
}
if(first[root]+second[root]>longest)//更新全局最大
longest=first[root]+second[root];
}
void init_first_second()
{
first.assign(n+1,0);
second.assign(n+1,0);
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
int a,b;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
f_s[a].push_back(b);//记录双边关系
f_s[b].push_back(a);//记录双边关系
}
init_first_second();
dfs(1,-1);//使用任意一个节点DFS，结果都是一样的。
/*int ans=0;
for(int i=1;i<=n;i++)//该循环可在DFS时完成
{
if(first[i]+second[i]>ans)
ans=first[i]+second[i];
}*/
cout<<longest;
return 0;
}
[/cpp]
本代码提交AC，用时224MS，内存9MB。
第二种方法不太好理解，所以还是建议大家用第一种方法。
网上关于树的直径介绍了3种方法，可以参考这篇文章。
]]>