hihoCoder week 52-1-连通性·一
题目1 : 连通性·一
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
还记得上次小Hi和小Ho学校被黑客攻击的事情么,那一次攻击最后造成了学校网络数据的丢失。为了避免再次出现这样的情况,学校决定对校园网络进行重新设计。
学校现在一共拥有N台服务器(编号1..N)以及M条连接,保证了任意两台服务器之间都能够通过连接直接或者间接的数据通讯。
当发生黑客攻击时,学校会立刻切断网络中的一条连接或是立刻关闭一台服务器,使得整个网络被隔离成两个独立的部分。
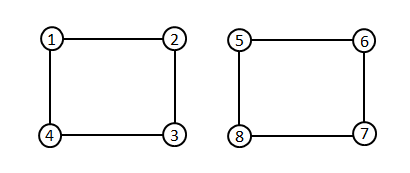
举个例子,对于以下的网络:
 每两个点之间至少有一条路径连通,当切断边(3,4)的时候,可以发现,整个网络被隔离为{1,2,3},{4,5,6}两个部分:
每两个点之间至少有一条路径连通,当切断边(3,4)的时候,可以发现,整个网络被隔离为{1,2,3},{4,5,6}两个部分:
 若关闭服务器3,则整个网络被隔离为{1,2},{4,5,6}两个部分:
若关闭服务器3,则整个网络被隔离为{1,2},{4,5,6}两个部分:
 小Hi和小Ho想要知道,在学校的网络中有哪些连接和哪些点被关闭后,能够使得整个网络被隔离为两个部分。
在上面的例子中,满足条件的有边(3,4),点3和点4。
提示:割边&割点
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:若干整数,用空格隔开,表示满足要求的服务器编号。从小到大排列。若没有满足要求的点,该行输出Null
第2..k行:每行2个整数,(u,v)表示满足要求的边,u<v。所有边根据u的大小排序,u小的排在前,当u相同时,v小的排在前面。若没有满足要求的边,则不输出
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3 4
3 4
小Hi和小Ho想要知道,在学校的网络中有哪些连接和哪些点被关闭后,能够使得整个网络被隔离为两个部分。
在上面的例子中,满足条件的有边(3,4),点3和点4。
提示:割边&割点
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:若干整数,用空格隔开,表示满足要求的服务器编号。从小到大排列。若没有满足要求的点,该行输出Null
第2..k行:每行2个整数,(u,v)表示满足要求的边,u<v。所有边根据u的大小排序,u小的排在前,当u相同时,v小的排在前面。若没有满足要求的边,则不输出
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3 4
3 4
本题要求一个连通图的割边和割点,使用Tarjan算法,提示已经把dfs主要代码写了,完善一下即可。
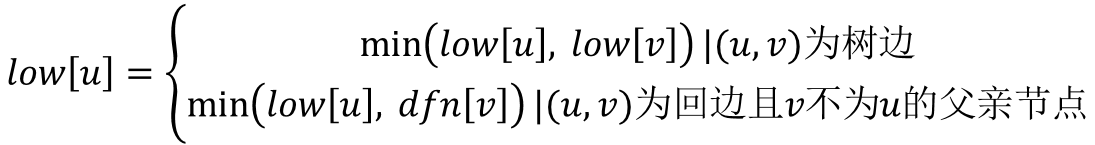 主要要理解上面的递推公式。首先理解dfn和low的含义,dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)。
上图的第一个式子,当(u,v)为树边时,low[u]表明u能追溯到的最早节点,low[v]表明u的子树(v就是u的子树的根)能追溯到的最早节点,所以根据low[u]的定义有low[u]=min(low[u],low[v])。
上图的第二个式子,当(u,v)为回边时,因为low[u]的定义就是u通过非父子边(回边)追溯最早的节点,所以既然(u,v)为回边,自然的low[u]=min(low[u],dfn[v])。
另外注意输出格式,点要从小到大排列;边(u,v)保证u<v,以u从小到大排列,再以v从小到大排列。完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<set>
#include<algorithm>
#include<vector>
using namespace std;
const int kMaxN = 20005;
int n, m;
typedef struct edge
{
int x, y;
bool operator<(const edge& p)const//如果要加入到set中,需要重载<
{
return (this->x<p.x) || ((this->x == p.x) && (this->y<p.y));
}
};
set<int> points;
set<edge> edges;
vector<vector<int>> graph;
int visit[kMaxN];
int dfn[kMaxN];
int low[kMaxN];
int parent[kMaxN];
void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;
//记录节点u的子树数
int children = 0;
visit[u] = 1;
//初始化dfn与low
dfn[u] = low[u] = ++counter;
for (int i = 0; i < graph[u].size();i++) {
int v = graph[u][i];
//节点v未被访问,则(u,v)为树边
if (visit[v]==0) {
children++;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if (parent[u] == 0 && children > 1) {
points.insert(u);
}
//case (2)
if (parent[u] != 0 && low[v] >= dfn[u]) {
points.insert(u);
}
//bridge
if (low[v] > dfn[u]) {
edge e;
e.x = u;
e.y = v;
if (u > v)
{
e.x = v;
e.y = u;
}
edges.insert(e);
}
}
//节点v已访问,则(u,v)为回边
else if (v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
scanf("%d %d", &n, &m);
graph.resize(n + 1);
int u, v;
while (m–)
{
scanf("%d %d", &u, &v);
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(1);
if (points.size() == 0)
printf("Null\n");
else
{
set<int>::iterator it = points.begin();
while (it != points.end())
{
printf("%d ", *it);
it++;
}
printf("\n");
}
if (edges.size() > 0)
{
set<edge>::iterator it = edges.begin();
while (it != edges.end())
{
printf("%d %d\n", (*it).x, (*it).y);
it++;
}
}
return 0;
}
[/cpp]
本代码提交AC,用时76MS,内存7MB。]]>
主要要理解上面的递推公式。首先理解dfn和low的含义,dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)。
上图的第一个式子,当(u,v)为树边时,low[u]表明u能追溯到的最早节点,low[v]表明u的子树(v就是u的子树的根)能追溯到的最早节点,所以根据low[u]的定义有low[u]=min(low[u],low[v])。
上图的第二个式子,当(u,v)为回边时,因为low[u]的定义就是u通过非父子边(回边)追溯最早的节点,所以既然(u,v)为回边,自然的low[u]=min(low[u],dfn[v])。
另外注意输出格式,点要从小到大排列;边(u,v)保证u<v,以u从小到大排列,再以v从小到大排列。完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<set>
#include<algorithm>
#include<vector>
using namespace std;
const int kMaxN = 20005;
int n, m;
typedef struct edge
{
int x, y;
bool operator<(const edge& p)const//如果要加入到set中,需要重载<
{
return (this->x<p.x) || ((this->x == p.x) && (this->y<p.y));
}
};
set<int> points;
set<edge> edges;
vector<vector<int>> graph;
int visit[kMaxN];
int dfn[kMaxN];
int low[kMaxN];
int parent[kMaxN];
void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;
//记录节点u的子树数
int children = 0;
visit[u] = 1;
//初始化dfn与low
dfn[u] = low[u] = ++counter;
for (int i = 0; i < graph[u].size();i++) {
int v = graph[u][i];
//节点v未被访问,则(u,v)为树边
if (visit[v]==0) {
children++;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if (parent[u] == 0 && children > 1) {
points.insert(u);
}
//case (2)
if (parent[u] != 0 && low[v] >= dfn[u]) {
points.insert(u);
}
//bridge
if (low[v] > dfn[u]) {
edge e;
e.x = u;
e.y = v;
if (u > v)
{
e.x = v;
e.y = u;
}
edges.insert(e);
}
}
//节点v已访问,则(u,v)为回边
else if (v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
scanf("%d %d", &n, &m);
graph.resize(n + 1);
int u, v;
while (m–)
{
scanf("%d %d", &u, &v);
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(1);
if (points.size() == 0)
printf("Null\n");
else
{
set<int>::iterator it = points.begin();
while (it != points.end())
{
printf("%d ", *it);
it++;
}
printf("\n");
}
if (edges.size() > 0)
{
set<edge>::iterator it = edges.begin();
while (it != edges.end())
{
printf("%d %d\n", (*it).x, (*it).y);
it++;
}
}
return 0;
}
[/cpp]
本代码提交AC,用时76MS,内存7MB。]]>
 这个机关是一个圆环,一共有2^N个区域,每个区域都可以改变颜色,在黑白两种颜色之间切换。
小Ho控制主角在周围探索了一下,果然又发现了一个纸片:
机关黑色的部分表示为1,白色的部分表示为0,逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布,使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次,终究没有办法打开,只得在此写下机关破解之法。
——By 无名的冒险者
小Ho:这什么意思啊?
小Hi:我给你举个例子,假如N=3,我们通过顺时针转动,可以使得正下方的3个区域表示为:
这个机关是一个圆环,一共有2^N个区域,每个区域都可以改变颜色,在黑白两种颜色之间切换。
小Ho控制主角在周围探索了一下,果然又发现了一个纸片:
机关黑色的部分表示为1,白色的部分表示为0,逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布,使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次,终究没有办法打开,只得在此写下机关破解之法。
——By 无名的冒险者
小Ho:这什么意思啊?
小Hi:我给你举个例子,假如N=3,我们通过顺时针转动,可以使得正下方的3个区域表示为:
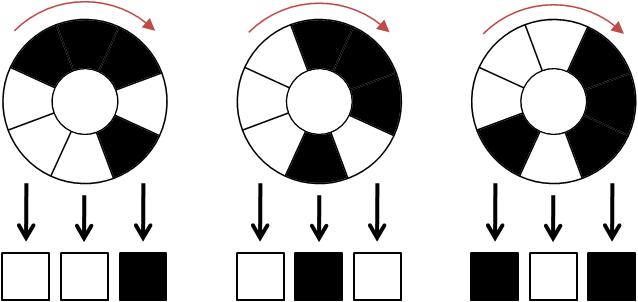 因为黑色表示为1,白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)
每转动一个区域,可以得到一个新的数字。一共可以转动2^N次,也就是2^N个数字。我们要调整黑白区域的位置,使得这2^N个数字恰好是0~2^N-1
小Ho:我懂了。若N=2,则将环上的黑白色块调整为”黑黑白白”,对应了”1100″。依次是”11″,”10″,”00″,”01″四个数字,正好是0~3。那么这个”黑黑白白”就可以打开机关了咯?
小Hi:我想应该是的。
小Ho:好像不是很难的样子,我来试试!
提示:有向图欧拉回路
输入
第1行:1个正整数,N。1≤N≤15
输出
第1行:1个长度为2^N的01串,表示一种符合要求的分布方案
样例输入
3
样例输出
00010111
因为黑色表示为1,白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)
每转动一个区域,可以得到一个新的数字。一共可以转动2^N次,也就是2^N个数字。我们要调整黑白区域的位置,使得这2^N个数字恰好是0~2^N-1
小Ho:我懂了。若N=2,则将环上的黑白色块调整为”黑黑白白”,对应了”1100″。依次是”11″,”10″,”00″,”01″四个数字,正好是0~3。那么这个”黑黑白白”就可以打开机关了咯?
小Hi:我想应该是的。
小Ho:好像不是很难的样子,我来试试!
提示:有向图欧拉回路
输入
第1行:1个正整数,N。1≤N≤15
输出
第1行:1个长度为2^N的01串,表示一种符合要求的分布方案
样例输入
3
样例输出
00010111
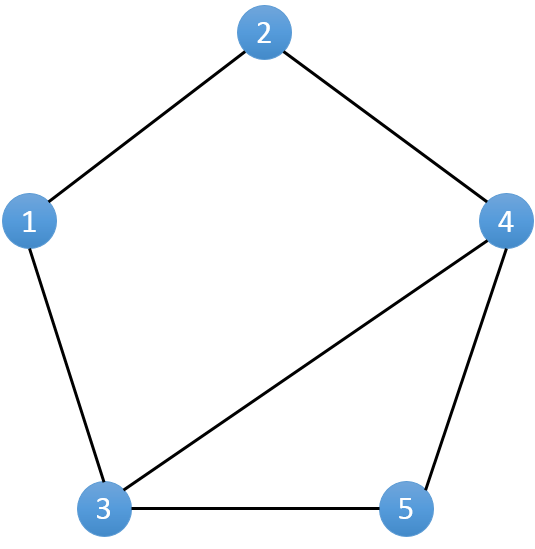 因为相亲总是在男女之间进行的,所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色,女性的节点染色黑色。对于得到的无向图来说,即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色,则表示这一条边所表示的记录有误。由于我们并不知道每个人的性别,我们的问题就转化为判定是否存在一个合理的染色方案,使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。那么,我们不妨将所有的点初始为未染色的状态。随机选择一个点,将其染成白色。再以它为起点,将所有相邻的点染成黑色。再以这些黑色的点为起点,将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)
因为相亲总是在男女之间进行的,所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色,女性的节点染色黑色。对于得到的无向图来说,即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色,则表示这一条边所表示的记录有误。由于我们并不知道每个人的性别,我们的问题就转化为判定是否存在一个合理的染色方案,使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。那么,我们不妨将所有的点初始为未染色的状态。随机选择一个点,将其染成白色。再以它为起点,将所有相邻的点染成黑色。再以这些黑色的点为起点,将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图) 在染色的过程中,我们应该怎样发现错误的记录呢?相信你一定发现了吧。对于一个已经染色的点,如果存在一个与它相邻的已染色点和它的颜色相同,那么就一定存在一条错误的记录。(如上图的4,5节点)到此我们就得到了整个图的算法:选取一个未染色的点u进行染色
遍历u的相邻节点v:若v未染色,则染色成与u不同的颜色,并对v重复第2步;若v已经染色,如果 u和v颜色相同,判定不可行退出遍历。
若所有节点均已染色,则判定可行。
接下来就动手写写吧!
输入
第1行:1个正整数T(1≤T≤10)
接下来T组数据,每组数据按照以下格式给出:
第1行:2个正整数N,M(1≤N≤10,000,1≤M≤40,000)
第2..M+1行:每行两个整数u,v表示u和v之间有一条边
输出
第1..T行:第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”,否则输出”Wrong”
样例输入
2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5
样例输出
Wrong
Correct
在染色的过程中,我们应该怎样发现错误的记录呢?相信你一定发现了吧。对于一个已经染色的点,如果存在一个与它相邻的已染色点和它的颜色相同,那么就一定存在一条错误的记录。(如上图的4,5节点)到此我们就得到了整个图的算法:选取一个未染色的点u进行染色
遍历u的相邻节点v:若v未染色,则染色成与u不同的颜色,并对v重复第2步;若v已经染色,如果 u和v颜色相同,判定不可行退出遍历。
若所有节点均已染色,则判定可行。
接下来就动手写写吧!
输入
第1行:1个正整数T(1≤T≤10)
接下来T组数据,每组数据按照以下格式给出:
第1行:2个正整数N,M(1≤N≤10,000,1≤M≤40,000)
第2..M+1行:每行两个整数u,v表示u和v之间有一条边
输出
第1..T行:第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”,否则输出”Wrong”
样例输入
2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5
样例输出
Wrong
Correct
 此图有两个连通分量,且两个分量都可以相亲成功,但如果只从第1点开始BFS,则不能遍历到第二个分量,导致失败。所以需要对每一个还未染色的点都开始BFS,如果都尝试过了还有点未染色,二分图判定失败;否则成功。
完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
int n, m;
vector<int> colored;
vector<vector<int>> path;
bool BFS(int start)
{
colored[start] = 0;
int num_colored = 1;
queue<int> point;
point.push(start);
while (!point.empty())
{
int current = point.front();
point.pop();
for (int i = 0; i < path[current].size(); i++)
{
if (colored[path[current][i]] == -1)
{
if (colored[current] == 0)
colored[path[current][i]] = 1;
else if (colored[current] == 1)
colored[path[current][i]] = 0;
num_colored++;
point.push(path[current][i]);
}
else if (colored[current] == colored[path[current][i]])
return false;
}
}
return true;
}
bool Check()
{
for (int i = 1; i <= n; i++)
if (colored[i] == -1)
if (!BFS(i))
return false;
return true;
}
int main()
{
int t,u,v;
scanf("%d", &t);
while (t–)
{
scanf("%d %d", &n, &m);
colored.clear();
colored.resize(n + 1, -1);
path.clear();
path.resize(n + 1);
for (int i = 0; i < m; i++)
{
scanf("%d %d", &u, &v);
path[u].push_back(v);
path[v].push_back(u);
}
if (Check())
printf("Correctn");
else
printf("Wrongn");
}
return 0;
}
[/cpp]
本代码提交AC,用时134MS,内存6MB。
]]>
此图有两个连通分量,且两个分量都可以相亲成功,但如果只从第1点开始BFS,则不能遍历到第二个分量,导致失败。所以需要对每一个还未染色的点都开始BFS,如果都尝试过了还有点未染色,二分图判定失败;否则成功。
完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
int n, m;
vector<int> colored;
vector<vector<int>> path;
bool BFS(int start)
{
colored[start] = 0;
int num_colored = 1;
queue<int> point;
point.push(start);
while (!point.empty())
{
int current = point.front();
point.pop();
for (int i = 0; i < path[current].size(); i++)
{
if (colored[path[current][i]] == -1)
{
if (colored[current] == 0)
colored[path[current][i]] = 1;
else if (colored[current] == 1)
colored[path[current][i]] = 0;
num_colored++;
point.push(path[current][i]);
}
else if (colored[current] == colored[path[current][i]])
return false;
}
}
return true;
}
bool Check()
{
for (int i = 1; i <= n; i++)
if (colored[i] == -1)
if (!BFS(i))
return false;
return true;
}
int main()
{
int t,u,v;
scanf("%d", &t);
while (t–)
{
scanf("%d %d", &n, &m);
colored.clear();
colored.resize(n + 1, -1);
path.clear();
path.resize(n + 1);
for (int i = 0; i < m; i++)
{
scanf("%d %d", &u, &v);
path[u].push_back(v);
path[v].push_back(u);
}
if (Check())
printf("Correctn");
else
printf("Wrongn");
}
return 0;
}
[/cpp]
本代码提交AC,用时134MS,内存6MB。
]]>
 主角继续往前走,面前出现了一座石桥,石桥的尽头有一道火焰墙,似乎无法通过。
小Hi注意到在桥头有一张小纸片,于是控制主角捡起了这张纸片,只见上面写着:
将M块骨牌首尾相连放置于石桥的凹糟中,即可关闭火焰墙。切记骨牌需要数字相同才能连接。
——By 无名的冒险者
小Hi和小Ho打开了主角的道具栏,发现主角恰好拥有M快骨牌。
小Ho:也就是说要把所有骨牌都放在凹槽中才能关闭火焰墙,数字相同是什么意思?
小Hi:你看,每一块骨牌两端各有一个数字,大概是只有当数字相同时才可以相连放置,比如:
主角继续往前走,面前出现了一座石桥,石桥的尽头有一道火焰墙,似乎无法通过。
小Hi注意到在桥头有一张小纸片,于是控制主角捡起了这张纸片,只见上面写着:
将M块骨牌首尾相连放置于石桥的凹糟中,即可关闭火焰墙。切记骨牌需要数字相同才能连接。
——By 无名的冒险者
小Hi和小Ho打开了主角的道具栏,发现主角恰好拥有M快骨牌。
小Ho:也就是说要把所有骨牌都放在凹槽中才能关闭火焰墙,数字相同是什么意思?
小Hi:你看,每一块骨牌两端各有一个数字,大概是只有当数字相同时才可以相连放置,比如:
 小Ho:原来如此,那么我们先看看能不能把所有的骨牌连接起来吧。
提示:Fleury算法求欧拉路径
输入
第1行:2个正整数,N,M。分别表示骨牌上出现的最大数字和骨牌数量。1≤N≤1,000,1≤M≤5,000
第2..M+1行:每行2个整数,u,v。第i+1行表示第i块骨牌两端的数字(u,v),1≤u,v≤N
输出
第1行:m+1个数字,表示骨牌首尾相连后的数字
比如骨牌连接的状态为(1,5)(5,3)(3,2)(2,4)(4,3),则输出”1 5 3 2 4 3″
你可以输出任意一组合法的解。
样例输入
5 5
3 5
3 2
4 2
3 4
5 1
样例输出
1 5 3 4 2 3
小Ho:原来如此,那么我们先看看能不能把所有的骨牌连接起来吧。
提示:Fleury算法求欧拉路径
输入
第1行:2个正整数,N,M。分别表示骨牌上出现的最大数字和骨牌数量。1≤N≤1,000,1≤M≤5,000
第2..M+1行:每行2个整数,u,v。第i+1行表示第i块骨牌两端的数字(u,v),1≤u,v≤N
输出
第1行:m+1个数字,表示骨牌首尾相连后的数字
比如骨牌连接的状态为(1,5)(5,3)(3,2)(2,4)(4,3),则输出”1 5 3 2 4 3″
你可以输出任意一组合法的解。
样例输入
5 5
3 5
3 2
4 2
3 4
5 1
样例输出
1 5 3 4 2 3
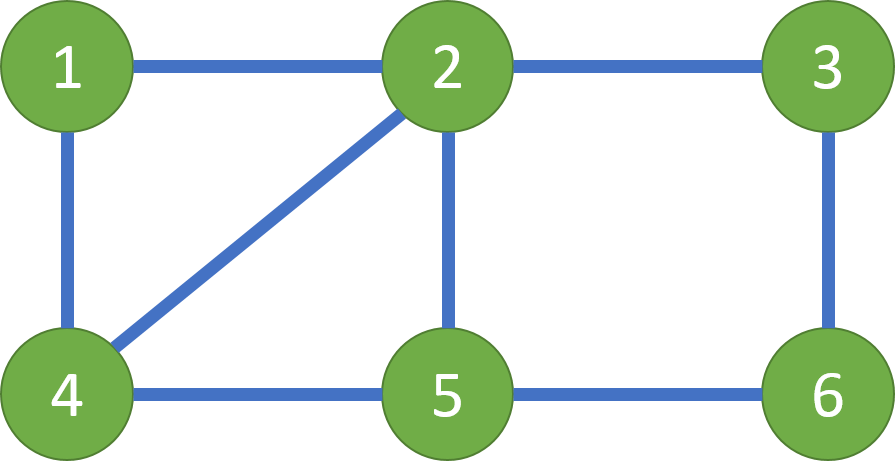 主角可以先到达4号小岛,然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛,然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。
提示:欧拉路的判定
输入
第1行:2个正整数,N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000,1≤M≤50,000
第2..M+1行:每行2个整数,u,v。表示有一座木桥连接着编号为u和编号为v的岛屿,两个岛之间可能有多座桥。1≤u,v≤N
输出
第1行:1个字符串,如果能收集齐所有的道具输出“Full”,否则输出”Part”。
样例输入
6 8
1 2
1 4
2 4
2 5
2 3
3 6
4 5
5 6
样例输出
Full
主角可以先到达4号小岛,然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛,然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。
提示:欧拉路的判定
输入
第1行:2个正整数,N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000,1≤M≤50,000
第2..M+1行:每行2个整数,u,v。表示有一座木桥连接着编号为u和编号为v的岛屿,两个岛之间可能有多座桥。1≤u,v≤N
输出
第1行:1个字符串,如果能收集齐所有的道具输出“Full”,否则输出”Part”。
样例输入
6 8
1 2
1 4
2 4
2 5
2 3
3 6
4 5
5 6
样例输出
Full