hihoCoder 1185-连通性·三
#1185 : 连通性·三
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
暑假到了!!小Hi和小Ho为了体验生活,来到了住在大草原的约翰家。今天一大早,约翰因为有事要出去,就拜托小Hi和小Ho忙帮放牧。
约翰家一共有N个草场,每个草场有容量为W[i]的牧草,N个草场之间有M条单向的路径。
小Hi和小Ho需要将牛羊群赶到草场上,当他们吃完一个草场牧草后,继续前往其他草场。当没有可以到达的草场或是能够到达的草场都已经被吃光了之后,小hi和小Ho就把牛羊群赶回家。
一开始小Hi和小Ho在1号草场,在回家之前,牛羊群最多能吃掉多少牧草?
举个例子:
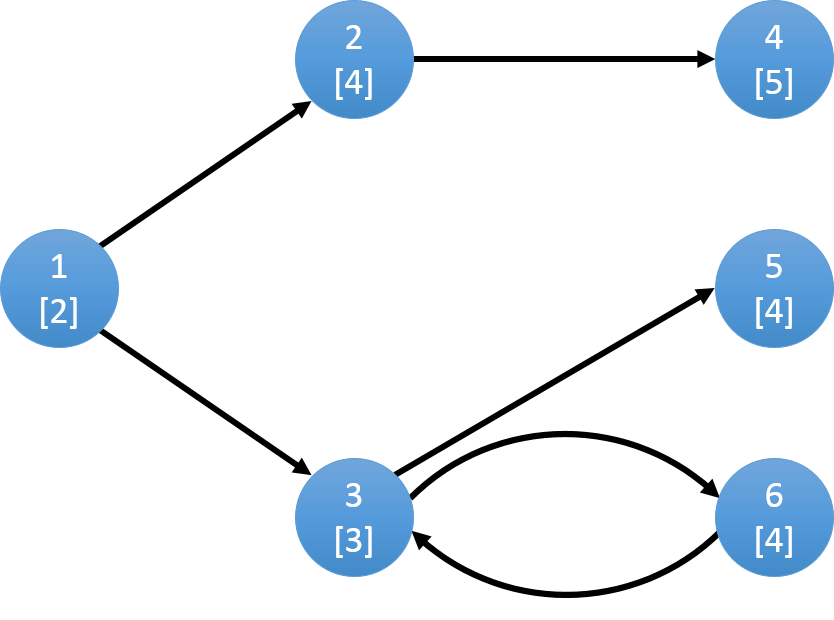 图中每个点表示一个草场,上部分数字表示编号,下部分表示草场的牧草数量w。
在1吃完草之后,小Hi和小Ho可以选择把牛羊群赶到2或者3,假设小Hi和小Ho把牛羊群赶到2:
吃完草场2之后,只能到草场4,当4吃完后没有可以到达的草场,所以小Hi和小Ho就把牛羊群赶回家。
若选择从1到3,则可以到达5,6:
选择5的话,吃完之后只能直接回家。若选择6,还可以再通过6回到3,再到5。
所以该图可以选择的路线有3条:
1->2->4 total: 11
1->3->5 total: 9
1->3->6->3->5 total: 13
所以最多能够吃到的牧草数量为13。
本题改编自USACO月赛金组
提示:强连通分量
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2行:N个正整数,第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000
第3..M+2行:2个正整数,u,v。表示存在一条从u到v的单向路径。1≤u,v≤N
输出
第1行:1个整数,最多能够吃到的牧草数量。
样例输入
6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3
样例输出
13
图中每个点表示一个草场,上部分数字表示编号,下部分表示草场的牧草数量w。
在1吃完草之后,小Hi和小Ho可以选择把牛羊群赶到2或者3,假设小Hi和小Ho把牛羊群赶到2:
吃完草场2之后,只能到草场4,当4吃完后没有可以到达的草场,所以小Hi和小Ho就把牛羊群赶回家。
若选择从1到3,则可以到达5,6:
选择5的话,吃完之后只能直接回家。若选择6,还可以再通过6回到3,再到5。
所以该图可以选择的路线有3条:
1->2->4 total: 11
1->3->5 total: 9
1->3->6->3->5 total: 13
所以最多能够吃到的牧草数量为13。
本题改编自USACO月赛金组
提示:强连通分量
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2行:N个正整数,第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000
第3..M+2行:2个正整数,u,v。表示存在一条从u到v的单向路径。1≤u,v≤N
输出
第1行:1个整数,最多能够吃到的牧草数量。
样例输入
6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3
样例输出
13
本题将图换成了有向图。首先求解有向图中的强连通分量,强连通分量是指有向图的子图中,两两点之间互相可达,求解方法和之前两道题的方法类似,还是用Tarjan算法,可以参考BYVoid的博客。 求解到所有强连通分量之后,将每个强连通分量缩成一个点,构成一个新的有向图,缩点的草量等于该强连通分量草量之和。 假设原图点1在新图中的缩点编号为u,则得到一个新的有向图之后,问题就转换为在新图中从点u开始遍历,求经过路径的草量之和最大是多少。这一步可以用常规DFS方法求解,也可以用提示中的拓扑排序求解,我觉得DFS更好理解一点。 完整代码如下: [cpp] #include<iostream> #include<cstdio> #include<queue> #include<algorithm> #include<vector> #include<stack> using namespace std; const int kMaxN = 20005; int n, m,new_n=0; stack<int> stk; vector<vector<int>> graph; vector<vector<int>> new_graph; int w[kMaxN]; int new_w[kMaxN]; int dfn[kMaxN];//DFS时的序号,如果!=0说明已经被访问过了 int low[kMaxN]; bool in_stack[kMaxN]; int belong[kMaxN]; int grass[kMaxN]; int in_degree[kMaxN]; bool visit[kMaxN]; int rs = 0; void Tarjan(int u) { //记录dfs遍历次序 static int counter = 0; stk.push(u); in_stack[u] = true; //初始化dfn与low dfn[u] = low[u] = ++counter; for (int i = 0; i < graph[u].size(); i++) { int v = graph[u][i]; //节点v未被访问 if (dfn[v] == 0) { Tarjan(v); low[u] = min(low[u], low[v]); } //节点v已访问,则(u,v)为回边 else if (in_stack[v]) { low[u] = min(low[u], dfn[v]); } } if (dfn[u] == low[u]) { new_n++; int temp; do{ temp = stk.top(); stk.pop(); new_w[new_n] += w[temp]; in_stack[temp] = false; belong[temp] = new_n; } while (temp != u); } } void RebuildGraph() { //重建邻接矩阵 new_graph.resize(new_n + 1); for (int i = 1; i <= n; i++) { for (int j = 0; j < graph[i].size(); j++) { if (belong[i] != belong[graph[i][j]]) { new_graph[belong[i]].push_back(belong[graph[i][j]]);//有边 in_degree[belong[graph[i][j]]]++; } } } } int TopSort() { queue<int> zero_in_degree; for (int i = 1; i <= new_n; i++) if (in_degree[i] == 0) zero_in_degree.push(i); int ans = 0; while (!zero_in_degree.empty()) { int node = zero_in_degree.front(); zero_in_degree.pop(); if (visit[node])//点belong[1]能访问到的点才计算,否则这步不执行,grass[node]为0 grass[node] += new_w[node]; if (grass[node] > ans) ans = grass[node]; for (int i = 0; i < new_graph[node].size(); i++) { int node2 = new_graph[node][i]; if (grass[node]>grass[node2]) grass[node2] = grass[node]; if (–in_degree[node2] == 0) zero_in_degree.push(node2); } } return ans; } //记录哪些点是belong[1]能访问到的 void Visit() { queue<int> q; q.push(belong[1]); while (!q.empty()) { int f = q.front(); q.pop(); visit[f] = true; for (int i = 0; i < new_graph[f].size(); i++) q.push(new_graph[f][i]); } } void DFS(int u,int g) { if (rs < g) rs = g; for (int i = 0; i < new_graph[u].size(); i++) DFS(new_graph[u][i], g + new_w[new_graph[u][i]]); } int main() { //freopen("input.txt", "r", stdin); scanf("%d %d", &n, &m); graph.resize(n + 1); for (int i = 1; i <= n; i++) scanf("%d", &w[i]); int u, v; while (m–) { scanf("%d %d", &u, &v); graph[u].push_back(v); } for (int i = 1; i <= n;i++)//每个点都要尝试一次 if (dfn[i]==0) Tarjan(i); RebuildGraph(); Visit(); printf("%dn", TopSort()); //深搜的方法也可以 //DFS(belong[1], new_w[belong[1]]); //printf("%dn", rs); return 0; } [/cpp] 本代码提交AC,用时57MS,内存3MB。 有两点需要注意:第一,因为有些点可能是1到达不了的,这样Tarjan(1)就不能得到所有的强连通分量,所以需要for循环尝试每一个点;第二,在拓扑排序的时候,如果某个缩点是belong[1]无法访问的,则其草量为0。]]>