5465. Number of Nodes in the Sub-Tree With the Same Label

Given a tree (i.e. a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. The root of the tree is the node 0, and each node of the tree has a label which is a lower-case character given in the string labels (i.e. The node with the number i has the label labels[i]).

The edges array is given on the form edges[i] = [ai, bi], which means there is an edge between nodes ai and bi in the tree.

Return an array of size n where ans[i] is the number of nodes in the subtree of the ith node which have the same label as node i.

A subtree of a tree T is the tree consisting of a node in T and all of its descendant nodes.

Example 1:

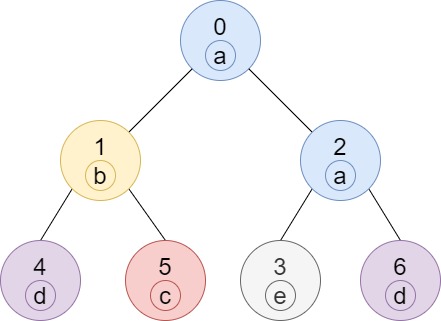
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
Output: [2,1,1,1,1,1,1]
Explanation: Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).

Example 2:

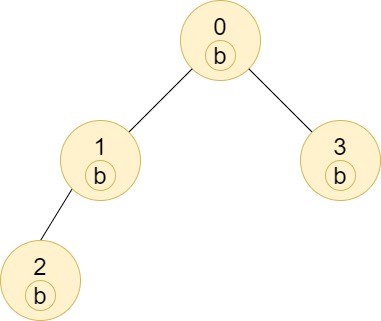
Input: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
Output: [4,2,1,1]
Explanation: The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.

Example 3:

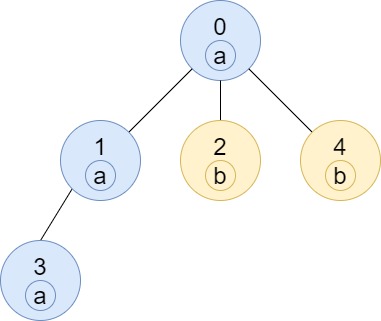
Input: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
Output: [3,2,1,1,1]

Example 4:

Input: n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa"
Output: [1,2,1,1,2,1]

Example 5:

Input: n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa"
Output: [6,5,4,1,3,2,1]

Constraints:

• 1 <= n <= 10^5
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• labels.length == n
• labels is consisting of only of lower-case English letters.

---

给定一棵多叉树（无向图），有n个顶点n-1条边。每个顶点上标了一个字母，问对于每个顶点，在它的子树中，与其字母相同的点有多少个。

每个节点维护一个26长的数组，记录该子树包含所有字母的频数。然后DFS，记录每个节点的这个数组，父节点的数组的值要累加上其直接孩子的这个数组的值。最后查表得到结果。代码如下：

class Solution {
private:
	void DFS(int parid, int curid, vector<vector<int>> &children_string, unordered_map<int, vector<int>> &graph, const string &labels) {
		int mylabel = labels[curid] - 'a';
		++children_string[curid][mylabel];

		for (int i = 0; i < graph[curid].size(); ++i) {
			int childid = graph[curid][i];
			if (childid == parid)continue;
			DFS(curid, childid, children_string, graph, labels);
			for (int j = 0; j < 26; ++j) {
				children_string[curid][j] += children_string[childid][j];
			}
		}
	}
public:
	vector<int> countSubTrees(int n, vector<vector<int>>& edges, string labels) {
		unordered_map<int, vector<int>> graph;
		for (int i = 0; i < edges.size(); ++i) {
			graph[edges[i][0]].push_back(edges[i][1]);
			graph[edges[i][1]].push_back(edges[i][0]);
		}
		vector<vector<int>> children_string(n, vector<int>(26, 0));
		
		DFS(-1, 0, children_string, graph, labels);

		vector<int> ans;
		for (int i = 0; i < n; ++i) {
			int mylabel = labels[i] - 'a';
			ans.push_back(children_string[i][mylabel]);
		}
		return ans;
	}
};

本代码提交AC。