LeetCode Leftmost Column with at Least a One

(This problem is an interactive problem.)

A binary matrix means that all elements are 0 or 1. For each individual row of the matrix, this row is sorted in non-decreasing order.

Given a row-sorted binary matrix binaryMatrix, return leftmost column index(0-indexed) with at least a 1 in it. If such index doesn’t exist, return -1.

You can’t access the Binary Matrix directly.  You may only access the matrix using a BinaryMatrix interface:

• BinaryMatrix.get(x, y) returns the element of the matrix at index (x, y) (0-indexed).
• BinaryMatrix.dimensions() returns a list of 2 elements [m, n], which means the matrix is m * n.

Submissions making more than 1000 calls to BinaryMatrix.get will be judged Wrong Answer.  Also, any solutions that attempt to circumvent the judge will result in disqualification.

For custom testing purposes you’re given the binary matrix mat as input in the following four examples. You will not have access the binary matrix directly.

Example 1:

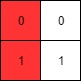
Input: mat = [[0,0],[1,1]]
Output: 0

Example 2:

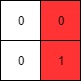
Input: mat = [[0,0],[0,1]]
Output: 1

Example 3:

Input: mat = [[0,0],[0,0]]
Output: -1

Example 4:

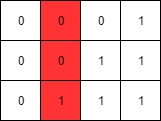
Input: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]]
Output: 1

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• mat[i][j] is either 0 or 1.
• mat[i] is sorted in a non-decreasing way.

---

给定一个0/1矩阵，且每行是升序排列的。问矩阵中至少包含一个1的列的最小列号。要求不能使用访问矩阵超过1k次，矩阵最大是100*100的。

常规解法。由于矩阵每行有序，所以在每一行中，使用二分搜索的方式找到1的最小下标，则所有行的最小下标的最小值即为答案。如果是m*n的矩阵，则时间复杂度为O(mlgn)。代码如下：

class Solution {
public:
	int LeftMost(BinaryMatrix &binaryMatrix, int row, int m, int n) {
		int l = 0, r = n - 1;
		while (l <= r) {
			int mid = l + (r - l) / 2;
			int midv = binaryMatrix.get(row, mid);
			if (midv == 0)l = mid + 1;
			else r = mid - 1;
		}
		return r + 1;
	}
	int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {
		vector<int> dim = binaryMatrix.dimensions();
		int m = dim[0], n = dim[1];
		int ans = n;
		for (int i = 0; i < m; ++i) {
			ans = min(ans, LeftMost(binaryMatrix, i, m, n));
		}
		if (ans == n)return -1;
		else return ans;
	}
};

本代码提交AC，用时8MS。

hint还提示了另一种解法，从矩阵的右上角开始，遇到0则往下走，遇到1则往左走。因为如果是1的话，至少当前所在列是包含1的，也许还可以再往左试探一下，而如果是0的话，只能往下走了。这种方法极端情况下可能从矩阵的右上角走到左下角，时间复杂度为O(m+n)。完整代码如下：

class Solution {
public:

	int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {
		vector<int> dim = binaryMatrix.dimensions();
		int m = dim[0], n = dim[1];
		int x = 0, y = n - 1;
		int ans = n;
		while (x < m&&y >= 0) {
			int val = binaryMatrix.get(x, y);
			if (val == 0)++x;
			else if (val == 1) {
				ans = y;
				if (y - 1 >= 0 && binaryMatrix.get(x, y - 1) == 1) {
					--y;
					ans = y;
				}
				else ++x;
			}
		}
		if (ans == n)return -1;
		else return ans;
	}
};

本代码提交AC，用时8MS。