POJ 1005-I Think I Need a Houseboat
I Think I Need a Houseboat
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 87833 Accepted: 38137
Description
Fred Mapper is considering purchasing some land in Louisiana to build his house on. In the process of investigating the land, he learned that the state of Louisiana is actually shrinking by 50 square miles each year, due to erosion caused by the Mississippi River. Since Fred is hoping to live in this house the rest of his life, he needs to know if his land is going to be lost to erosion.
After doing more research, Fred has learned that the land that is being lost forms a semicircle. This semicircle is part of a circle centered at (0,0), with the line that bisects the circle being the X axis. Locations below the X axis are in the water. The semicircle has an area of 0 at the beginning of year 1. (Semicircle illustrated in the Figure.)
Input
The first line of input will be a positive integer indicating how many data sets will be included (N). Each of the next N lines will contain the X and Y Cartesian coordinates of the land Fred is considering. These will be floating point numbers measured in miles. The Y coordinate will be non-negative. (0,0) will not be given.
Output
For each data set, a single line of output should appear. This line should take the form of: “Property N: This property will begin eroding in year Z.” Where N is the data set (counting from 1), and Z is the first year (start from 1) this property will be within the semicircle AT THE END OF YEAR Z. Z must be an integer. After the last data set, this should print out “END OF OUTPUT.”
Sample Input
2
1.0 1.0
25.0 0.0
Sample Output
Property 1: This property will begin eroding in year 1.
Property 2: This property will begin eroding in year 20.
END OF OUTPUT.
Hint
1.No property will appear exactly on the semicircle boundary: it will either be inside or outside.
2.This problem will be judged automatically. Your answer must match exactly, including the capitalization, punctuation, and white-space. This includes the periods at the ends of the lines.
3.All locations are given in miles.
Source
Mid-Atlantic 2001
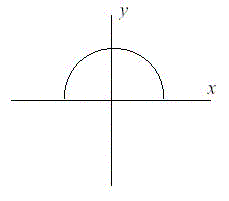
这题也不难，常规数学题，侵蚀面积以每年50平方米的速度进行，可以由此算出每年之后总的侵蚀面积的半径，然后通过比较给出的x、y到原点的距离判断是否在侵蚀面积之内。具体代码如下： [cpp] #include<iostream> #include<string> #include<cmath> using namespace std; double R[100];//Fred is hoping to live in this house the rest of his life.余生最多设为100年 //初始化 void init() { for(int i=0;i<100;i++) { R[i]=sqrt(2*50*(i+1)/3.14); } } //二分查找 int bin_search(double r) { int start=0,end=99,mid; while(start<=end) { mid=(start+end)/2; if(R[mid]>r) end=mid-1; else start=mid+1; } //这个时候start==end if(R[start]<r) return start+1; else return start; } int main() { init(); int n; double x,y; cin>>n; for(int i=1;i<=n;i++) { cin>>x>>y; double r=sqrt(x*x+y*y); cout<<"Property "<<i<<": This property will begin eroding in year "<<bin_search(r)+1<<"."<<endl; } cout<<"END OF OUTPUT."; return 0; } [/cpp] 本代码提交AC，用时0MS，内存220K。]]>