145. Binary Tree Postorder Traversal

Given a binary tree, return the postorder traversal of its nodes’ values.

Example:

Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [3,2,1]

Follow up: Recursive solution is trivial, could you do it iteratively?

---

实现二叉树的后续遍历算法，需要非递归形式哦~这题好难…是三种非递归遍历算法中最难的一种了。
惯例，先上递归算法：

class Solution {
public:
    void work(vector<int>& ans, TreeNode* root)
    {
        if (root == NULL)
            return;
        work(ans, root->left);
        work(ans, root->right);
        ans.push_back(root->val);
    }
    vector<int> postorderTraversal(TreeNode* root)
    {
        vector<int> ans;
        work(ans, root);
        return ans;
    }
};

本代码提交AC，用时3MS。
下面来想非递归算法。后续遍历的顺序是：左右根，根节点是最后访问的。还是用堆栈来实现，那么根据堆栈的后进先出性质，压栈的顺序应该是根右左。
那么什么时候可以访问根节点呢，只有当这个节点是叶子节点或者左右孩子都访问完之后才可以。判断是否为叶子节点很容易，那么怎么判断左右孩子都访问完了呢，此时我们可以用一个变量pre来记录上一次访问的节点，curr为当前栈顶节点。如果pre是curr的左或右孩子节点，则说明左右孩子已经访问过了，此时我们就可以访问curr了。
本算法的代码如下：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root)
    {
        vector<int> ans;
        if (root == NULL)
            return ans;
        stack<TreeNode*> tree;
        TreeNode *curr, *pre = NULL;
        tree.push(root); // 根
        while (!tree.empty()) {
            curr = tree.top();
            if ((curr->left == NULL && curr->right == NULL) || // 已到叶子节点
                (pre != NULL && (curr->left == pre || curr->right == pre))) { // 回溯的时候
                ans.push_back(curr->val);
                tree.pop();
                pre = curr;
            }
            else {
                if (curr->right != NULL)
                    tree.push(curr->right); // 右
                if (curr->left != NULL)
                    tree.push(curr->left); // 左
            }
        }
        return ans;
    }
};

本代码提交AC，用时0MS。

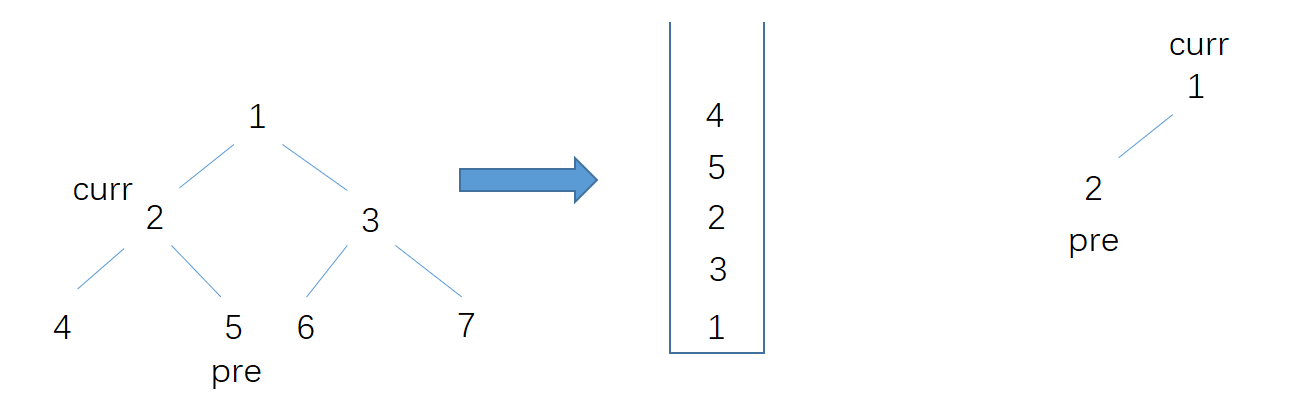
可能有同学担心curr->left==pre不能一定说明左右孩子都访问完了，只能说明左孩子访问完了。但是根据我们的压栈顺序，当curr同时又左右孩子的时候，不会走这条判断。如下左图所示，首先4会弹栈，然后栈顶变为了5，此时pre=4, curr=5，访问5；然后5弹栈，栈顶为2，此时pre=5,curr=2，所以走的是curr->right==pre，访问2。只有当curr只有左孩子没有右孩子的时候才会判断curr->left==pre，如下右图，此时是可以访问curr的。

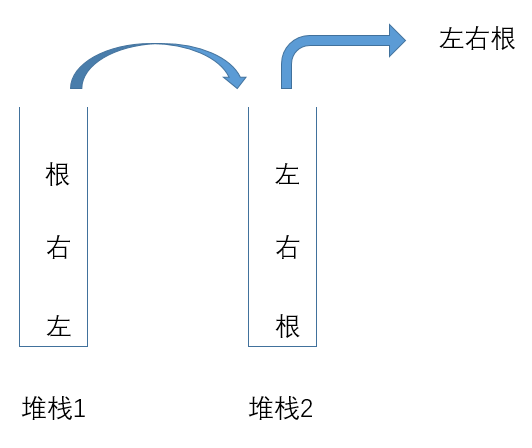
还有一种很简洁漂亮的解法，用两个堆栈。再次回忆后序遍历顺序：左右根，我们怎样用两个堆栈得到这样的顺序呢。如下图所示，第一个堆栈压栈顺序是左右根，然后弹出来压到第二个堆栈里，则从第二个堆栈里弹出来的顺序就是左右根了。注意，虽然第一次压栈的顺序已经是左右根了，我们要得到的也是左右根，为什么还要经过第二个堆栈这样倒腾一下呢？因为堆栈1的左右根和从堆栈2出来的左右根是不一样的，前者是靠近根节点的左右根，但是我们的后序遍历是要从叶子节点开始得到左右根，而从堆栈2出来的就是从叶子节点开始的左右根。

下面结合代码来说：

 class Solution {
   public: vector < int > postorderTraversal(TreeNode * root) {
     vector < int > ans;
     if (root == NULL) return ans;
     stack < TreeNode * > s1, s2;
     TreeNode * top;
     s1.push(root); // 根 
     while (!s1.empty()) {
       top = s1.top(); // (1)
       s1.pop(); // (1)
       s2.push(top); // (1)
       if (top - > left != NULL) {
         // 左
         s1.push(top - > left);
       }
       if (top - > right != NULL) {
         // 右 
         s1.push(top - > right);
       }
     }
     while (!s2.empty()) {
       top = s2.top();
       ans.push_back(top - > val);
       s2.pop();
     }
     return ans;
   }
 };

从第13、16行可知，对于堆栈1，我们先压了左后压了右，但是从第8行来看，根是最先压的，看起来不符合左右根的压栈顺序，但是请注意，代码(1)部分在先于13、16行弹栈了，然后马上压到堆栈2了，这样的效果不就是根节点在堆栈1的栈顶，然后被压到了堆栈2的底部了吗。所以和上图是统一的。

本代码提交AC，用时0MS。
定睛一看，这居然是道hard题。。。

三刷。这一题和中序遍历的迭代解法很类似。后序遍历是左右根，依然是要最先访问左子树的左叶子，所以依然可以使用函数putAllLeft将根沿着左子树的节点都放到栈中，只是在弹栈访问时，需要注意，如果该节点的右孩子已经访问，则无需再调用putAllLeft了，否则会导致死循环。所以在访问某个节点时，记录一下，存到pre中，作为下一个节点访问时上一个访问的节点。如果当前要访问的右孩子为pre，则说明右孩子已经访问过了，无需对右孩子调用putAllLeft。

完整代码如下：

class Solution {
public:
	void PutAllLeft(TreeNode *root, stack<TreeNode*> &stk) {
		while (root != NULL) {
			stk.push(root);
			root = root->left;
		}
	}
	vector<int> postorderTraversal(TreeNode* root) {
		vector<int> ans;
		stack<TreeNode*> stk;
		PutAllLeft(root, stk);
		TreeNode *pre = NULL;
		while (!stk.empty()) {
			TreeNode *cur = stk.top();
			if (cur->right != NULL && cur->right != pre) {
				PutAllLeft(cur->right, stk);
			}
			else {
				ans.push_back(cur->val);
				stk.pop();
				pre = cur;
			}
		}
		return ans;
	}
};

本代码提交AC，用时0MS。