hihoCoder 1552-缺失的拼图
#1552 : 缺失的拼图
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi在玩一个拼图游戏。如下图所示，整个拼图是由N块小矩形组成的大矩形。现在小Hi发现其中一块小矩形不见了。给定大矩形以及N-1个小矩形的顶点坐标，你能找出缺失的那块小矩形的顶点坐标吗？
输入
第一行包含一个整数，N。 第二行包含四个整数，(X0, Y0), (X‘0, Y‘0)，代表大矩形左下角和右上角的坐标。 以下N-1行每行包含四个整数，(Xi, Yi), (X‘i, Y‘i)，代表其中一个小矩形的左下角和右上角坐标。 对于30%的数据， 1 <= N <= 1000 对于100%的数据，1 <= N <= 100000 所有的坐标(X, Y)满足 0 <= X, Y <= 100000000输出
输出四个整数(X, Y), (X‘, Y‘)代表缺失的那块小矩形的左下角和右上角的坐标。- 样例输入
-
5 0 0 4 5 0 0 3 1 0 1 2 5 3 0 4 5 2 2 3 5
- 样例输出
-
2 1 3 2
一个矩形由N个小矩形拼接而成，现在丢了一个小矩形，怎样才能找到这个小矩形呢。所有矩形都用左下角坐标和右上角坐标表示。 这一题也很有意思，丢掉的那个小矩形的坐标肯定是其他N-1个矩形的坐标中的某4个。我们可以统计每个坐标点出现的次数，如果出现偶数次，则这个点所在的矩形是出现过的，否则这个点就是缺失矩形的某个顶点。最后，从缺失的4个顶点中找出左下角坐标和右上角坐标。 完整代码如下： [cpp] #include<algorithm> #include<vector> #include<iostream> #include<unordered_map> #include<unordered_set> #include<string> #include<set> #include<map> #include<queue> using namespace std; typedef long long ll; typedef pair<int, int> Point; int main() { //freopen("input.txt", "r", stdin); int n; scanf("%d", &n); map<Point, int> hash; int a, b, c, d; while (n–) { Point left_bottom, right_top; scanf("%d %d %d %d", &left_bottom.first, &left_bottom.second, &right_top.first, &right_top.second); Point left_top = Point(left_bottom.first, right_top.second), right_bottom = Point(right_top.first, left_bottom.second); ++hash[left_bottom]; ++hash[right_top]; ++hash[left_top]; ++hash[right_bottom]; } set<Point> ans; for (auto p : hash) { if (p.second % 2 == 1) { ans.insert(p.first); } } a = c = ans.begin()->first; b = d = ans.begin()->second; for (auto p : ans) { a = min(a, p.first); b = min(b, p.second); c = max(c, p.first); d = max(d, p.second); } printf("%d %d %d %d\n", a, b, c, d); return 0; } [/cpp] 本代码提交AC，用时432MS。]]>
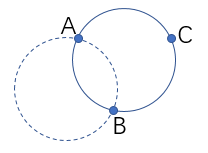已知两点求圆心的方法请看
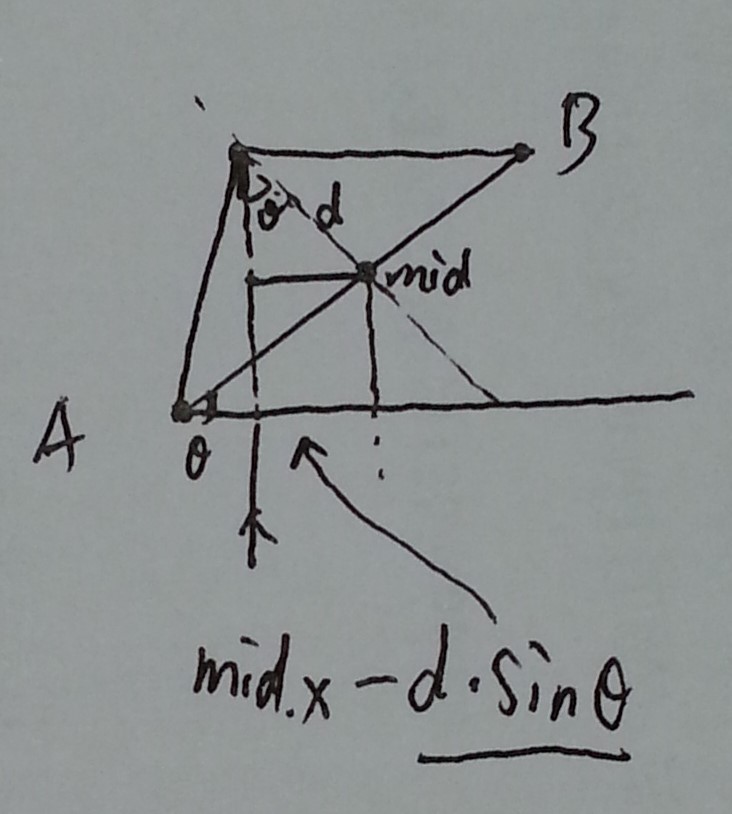暴力方法在hiho上TLE，需要寻求更高效的算法。
假设以两个点i,j为圆心画半径为R的圆，如果两个圆相交，则在相交的弧上任意一点画圆，都能覆盖原来的i,j两点。基于这个思想，假设现在固定点i为圆心，R为半径画圆，求出所有以其他点为圆心画的圆和圆i相交的弧，则在相交重叠次数最多的那段弧上的点为圆心画的圆肯定能覆盖最多的点，覆盖的点数就是这段弧被重叠的次数。每个点i都能求出这样一个最大值，则所有点的这个最大值的最大值就是全局能覆盖的最多点。
怎样表示两个圆相交的那段弧呢，使用极坐标，因为弧是由两条半径张成的，所以可以表示成两条半径的极坐标夹角，并且标明夹角的开始（is=1）和结束（is=-1）。求重叠次数最多的弧的方法是，把所有重叠弧的起止半径的极坐标夹角排个序，然后遍历一下，当夹角开始（is=1）次数最多且结束（is=-1）次数最少时，说明重叠次数最多，所以就是is的累加和的最大值。
完整代码借鉴