hihoCoder 1087 & week 63-1-Hamiltonian Cycle #1087 : Hamiltonian Cycle 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 Given a directed graph containing n vertice (numbered from 1 to n) and m edges. Can you tell us how many different Hamiltonian Cycles are there in this graph? A Hamiltonian Cycle is a cycle that starts from some vertex, visits each vertex (except for the start vertex) exactly once, and finally ends at the start vertex. Two Hamiltonian Cycles C1, C2 are different if and only if there exists some vertex i that, the next vertex of vertex i in C1 is different from the next vertex of vertex i in C2. 输入 The first line contains two integers n and m. 2 <= n <= 12, 1 <= m <= 200. Then follows m line. Each line contains two different integers a and b, indicating there is an directed edge from vertex a to vertex b. 输出 Output an integer in a single line — the number of different Hamiltonian Cycles in this graph. 提示 额外的样例:
| 样例输入 | 样例输出 |
| 3 3 1 2 2 1 1 3 | 0 |
本题要求解一个有向图中存在多少个哈密顿回路,因为本题的n不超过12,所以可以暴力求解,但是可以用位运算和记忆化搜索提高搜索速度。 常规思路是从某一点DFS,计算所有哈密顿回路的数量,伪代码如下: [cpp] DFS(int nowVertex, bool visitedVertex, int path, int length) visitedVertex[ nowVertex ] = True; If (all Vertex is visited) Then Count = Count + 1 Else For (u is next vertex of nowVertex) If (not visitedVertex[ u ]) Then path[ length ] = u DFS(u, visitedVertex, path, length + 1) End If End For End If visitedVertex[ nowVertex ] = False [/cpp] 位运算的思路是用变量unused的二进制位表示一个点是否访问过,1未访问,0访问了。所以当DFS到unused==0时,找到一条哈密顿路径,如果该路径的终点能回到起点(默认为1),则构成一条哈密顿回路。部分代码如下: [cpp] const int MAXN = 14; int edge[ MAXN ];//edge[i]二进制中1的序号表示i能访问的节点编号 int p[1 << MAXN];//p[1<<i]=i+1表示只有i点访问了的情况为1<<i int cnt; void dfs(int nowVertex, int unused) { if (!unused) {//所有节点访问完了 cnt += (edge[nowVertex] & 1);//判断能否回到起始节点1 return ; } int rest = unused & edge[ nowVertex ];//剩余的能访问到的未访问节点 while (rest) { int tp = rest & (-rest);//依次取出可访问节点 dfs(p[ tp ], unused – tp);//访问 rest -= tp; } return ; } int main() { int n, m; scanf("%d %d", &n, &m); for (int i = 0; i < n; ++i) p[ 1 << i ] = i + 1; while (m–) { int u, v; scanf("%d %d", &u, &v); edge[u] |= 1 << (v – 1);//记录u能访问节点的情况 } dfs(1, (1 << n) – 2);//初始的时候访问了1号节点,所以-1-1=-2 printf("%d\n", cnt); return 0; } [/cpp] 这一版本的代码简洁易懂,效率也还可以,用时558MS,内存0MB。 但是还可以改进,在DFS过程中可能遇到某个节点的多次unused相同的情况,此时后面几次的DFS都是没有必要的,可以剪枝。 设f[i][j]为当前访问节点为i,已经访问过的节点情况为j时的方案数,则哈密顿路径的情况数为f[i][0],i在[1,n],哈密顿回路的情况数就是把所有i能回到1的f[i][0]情况数加起来。 那么怎么来计算f[i][j]呢,需要按照状态中1的个数来枚举,伪代码如下: [cpp] For numberOfOnes = n-1 .. 0 For (unused | the number of ones of unused equals numberOfOnes) For nowVertex = 1 .. n For prevVertex = 1 .. n If (unused & (1 << (nowVertex – 1)) == 0) and (prevVertex != nowVertex) and (edge[ prevVertex ] & (1 << (nowVertex – 1)) != 0) Then f[ nowVertex ][ unused ] = f[ nowVertex ][ unused ] + f[ prevVertex ][unused + (1 << (nowVertex – 1))] End If End For End For End For End For [/cpp] 第二层for循环中的unused就是所有“在n位二进制中设置numberOfOnes位1”的所有状态,最内层的if判断该状态必须满足1)已经访问了当前节点2)前驱节点不等于当前节点3)前驱节点有到当前节点的边,则f[当前节点][访问情况为unused]+=f[前驱节点][访问情况为unused+还没访问当前节点]。 详细分析可以看官方题解。完整代码如下: [cpp] #include<iostream> #include<cstdio> #include<vector> #include<iterator> using namespace std; const int MAXN = 14; int edge[MAXN]; int p[1 << MAXN]; int f[MAXN][1<<MAXN]; //n位二进制中出现k个1的所有排列情况 vector<int> dfs(int n, int k) { if (k == 0)//出现0个1,只有一种情况,全0 return vector<int>(1, 0); else { //********** n==k的情况 ************************** vector<int> r = dfs(n – 1, k – 1);//n-1位中出现k-1个1//将大问题分解成小问题 for (int &i : r) { i |= (1 << (n – 1));//补上第n位也为1 } //************************************************** if (n > k) { vector<int> t = dfs(n – 1, k);//此时第n位可以为0 copy(t.begin(), t.end(), back_inserter(r)); } return r; } } int main() { //freopen("input.txt", "r", stdin); int n, m; scanf("%d %d", &n, &m); for (int i = 0; i < n; ++i) p[1 << i] = i + 1; while (m–) { int u, v; scanf("%d %d", &u, &v); edge[u] |= 1 << (v – 1); } f[1][(1 << n) – 2] = 1; for (int numberOfOnes = n – 1; numberOfOnes >= 0; numberOfOnes–) { vector<int> stat = dfs(n, numberOfOnes); for (int i = 0; i < stat.size(); i++) { int s = stat[i]; for (int nowVertex = 1; nowVertex <= n; nowVertex++) { for (int prevVertex = 1; prevVertex <= n; prevVertex++) { if ((s & (1 << (nowVertex – 1))) == 0 && prevVertex != nowVertex && (edge[prevVertex] & (1 << (nowVertex – 1))) != 0) f[nowVertex][s] += f[prevVertex][s | (1 << (nowVertex – 1))]; } } } } int cnt = 0; for (int i = 1; i <= n; i++) if (edge[i] & 1) cnt += f[i][0]; printf("%d\n", cnt); return 0; } [/cpp] 本代码提交AC,用时21MS,内存0MB,相比于上一版本,速度提升了一个数量级。]]>
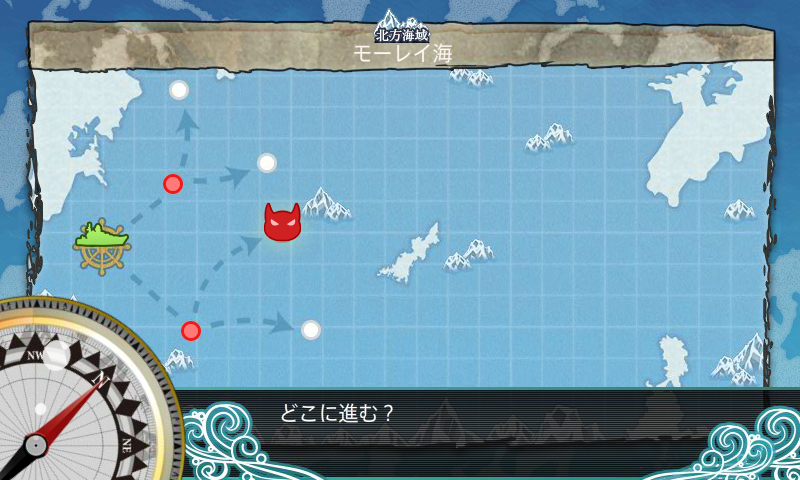 其中红色的点表示有敌人驻扎,猫头像的的点表示该地图敌军主力舰队(boss)的驻扎点,虚线表示各个战略点之间的航线(无向边)。
在游戏中要从一个战略点到相邻战略点需要满足一定的条件,即需要舰队的索敌值大于等于这两点之间航线的索敌值需求。
由于提高索敌值需要将攻击机、轰炸机换成侦察机,舰队索敌值越高,也就意味着舰队的战力越低。
另外在每一个战略点会发生一次战斗,需要消耗1/K的燃料和子弹。必须在燃料和子弹未用完的情况下进入boss点才能与boss进行战斗,所以舰队最多只能走过K条航路。
现在Nettle想要以最高的战力来进攻boss点,所以他希望能够找出一条从起始点(编号为1的点)到boss点的航路,使得舰队需要达到的索敌值最低,并且有剩余的燃料和子弹。
特别说明:两个战略点之间可能不止一条航线,两个相邻战略点之间可能不止一条航线。保证至少存在一条路径能在燃料子弹用完前到达boss点。
提示:你在找什么?
输入
第1行:4个整数N,M,K,T。N表示战略点数量,M表示航线数量,K表示最多能经过的航路,T表示boss点编号, 1≤N,K≤10,000, N≤M≤100,000
第2..M+1行:3个整数u,v,w,表示战略点u,v之间存在航路,w表示该航路需求的索敌值,1≤w≤1,000,000。
输出
第1行:一个整数,表示舰队需要的最小索敌值。
样例输入
5 6 2 5
1 2 3
1 3 2
1 4 4
2 5 2
3 5 5
4 5 3
样例输出
3
其中红色的点表示有敌人驻扎,猫头像的的点表示该地图敌军主力舰队(boss)的驻扎点,虚线表示各个战略点之间的航线(无向边)。
在游戏中要从一个战略点到相邻战略点需要满足一定的条件,即需要舰队的索敌值大于等于这两点之间航线的索敌值需求。
由于提高索敌值需要将攻击机、轰炸机换成侦察机,舰队索敌值越高,也就意味着舰队的战力越低。
另外在每一个战略点会发生一次战斗,需要消耗1/K的燃料和子弹。必须在燃料和子弹未用完的情况下进入boss点才能与boss进行战斗,所以舰队最多只能走过K条航路。
现在Nettle想要以最高的战力来进攻boss点,所以他希望能够找出一条从起始点(编号为1的点)到boss点的航路,使得舰队需要达到的索敌值最低,并且有剩余的燃料和子弹。
特别说明:两个战略点之间可能不止一条航线,两个相邻战略点之间可能不止一条航线。保证至少存在一条路径能在燃料子弹用完前到达boss点。
提示:你在找什么?
输入
第1行:4个整数N,M,K,T。N表示战略点数量,M表示航线数量,K表示最多能经过的航路,T表示boss点编号, 1≤N,K≤10,000, N≤M≤100,000
第2..M+1行:3个整数u,v,w,表示战略点u,v之间存在航路,w表示该航路需求的索敌值,1≤w≤1,000,000。
输出
第1行:一个整数,表示舰队需要的最小索敌值。
样例输入
5 6 2 5
1 2 3
1 3 2
1 4 4
2 5 2
3 5 5
4 5 3
样例输出
3
 输入
The first line contains an integer T, the number of test cases. T test cases follows.
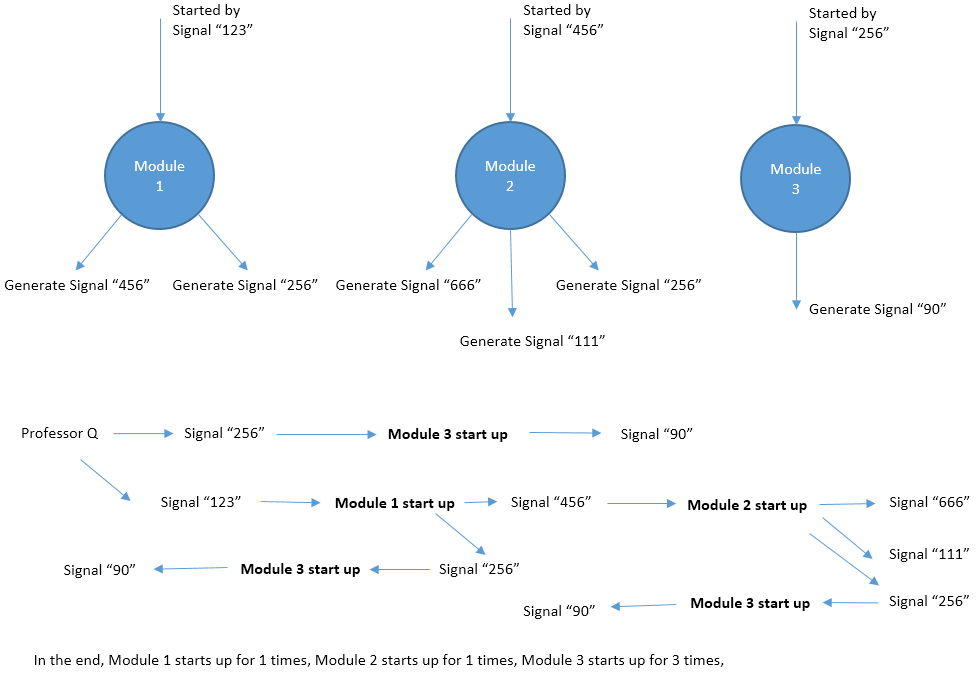
For each test case, the first line contains contains two numbers N and M, indicating the number of modules and number of signals that Professor Q generates initially.
The second line contains M integers, indicating the signals that Professor Q generates initially.
Line 3~N + 2, each line describes an module, following the format S, K, E1, E2, … , EK. S represents the signal that start up this module. K represents the total amount of signals that are generated during the lifecircle of this module. And E1 … EK are these signals.
For 20% data, all N, M <= 10
For 40% data, all N, M <= 103
For 100% data, all 1 <= T <= 5, N, M <= 105, 0 <= K <= 3, 0 <= S, E <= 105.
Hint: HUGE input in this problem. Fast IO such as scanf and BufferedReader are recommended.
输出
For each test case, output a line with N numbers Ans1, Ans2, … , AnsN. Ansi is the number of times that the i-th module is started. In case the answers may be too large, output the answers modulo 142857 (the remainder of division by 142857).
样例输入
3
3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90
3 1
100
100 2 200 200
200 1 300
200 0
5 1
1
1 2 2 3
2 2 3 4
3 2 4 5
4 2 5 6
5 2 6 7
样例输出
1 1 3
1 2 2
1 1 2 3 5
输入
The first line contains an integer T, the number of test cases. T test cases follows.
For each test case, the first line contains contains two numbers N and M, indicating the number of modules and number of signals that Professor Q generates initially.
The second line contains M integers, indicating the signals that Professor Q generates initially.
Line 3~N + 2, each line describes an module, following the format S, K, E1, E2, … , EK. S represents the signal that start up this module. K represents the total amount of signals that are generated during the lifecircle of this module. And E1 … EK are these signals.
For 20% data, all N, M <= 10
For 40% data, all N, M <= 103
For 100% data, all 1 <= T <= 5, N, M <= 105, 0 <= K <= 3, 0 <= S, E <= 105.
Hint: HUGE input in this problem. Fast IO such as scanf and BufferedReader are recommended.
输出
For each test case, output a line with N numbers Ans1, Ans2, … , AnsN. Ansi is the number of times that the i-th module is started. In case the answers may be too large, output the answers modulo 142857 (the remainder of division by 142857).
样例输入
3
3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90
3 1
100
100 2 200 200
200 1 300
200 0
5 1
1
1 2 2 3
2 2 3 4
3 2 4 5
4 2 5 6
5 2 6 7
样例输出
1 1 3
1 2 2
1 1 2 3 5