hihoCoder 1062-最近公共祖先·一 #1062 : 最近公共祖先·一 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 小Ho最近发现了一个神奇的网站！虽然还不够像58同城那样神奇，但这个网站仍然让小Ho乐在其中，但这是为什么呢？ “为什么呢？”小Hi如是问道，在他的观察中小Ho已经沉迷这个网站一周之久了，甚至连他心爱的树玩具都弃置一边。 “嘿嘿，小Hi，你快过来看！”小Ho招呼道。 “你看，在这个对话框里输入我的名字，在另一个对话框里，输入你的名字，再点这个查询按钮，就可以查出来……什么！我们居然有同一个祖祖祖祖祖爷爷？” “诶，真是诶……这个网站有点厉害啊。”小Hi不由感叹道。 “是啊，这是什么算法啊，这么厉害！”小Ho也附和道。 “别2，我说的是他能弄到这些数据很厉害，而人类的繁殖树这种层数比较浅的树对这类算法的要求可是简单的不得了，你都能写出来呢！”小Hi道。 “啊？我也能写出来？可是……该从哪开始呢？”小Ho困惑了。 小Ho要面临的问题是这样的，假设现在他知道了N个人的信息——他们的父亲是谁，他需要对于小Hi的每一次提问——两个人的名字，告诉小Hi这两个人的是否存在同一个祖先，如果存在，那么他们的所有共同祖先中辈分最低的一个是谁？ 提示：不着急，慢慢来，另外我有一个问题：挖掘机技术哪家强？！ 输入 每个测试点（输入文件）有且仅有一组测试数据。 每组测试数据的第1行为一个整数N，意义如前文所述。 每组测试数据的第2~N+1行，每行分别描述一对父子关系，其中第i+1行为两个由大小写字母组成的字符串Father_i, Son_i，分别表示父亲的名字和儿子的名字。 每组测试数据的第N+2行为一个整数M，表示小Hi总共询问的次数。 每组测试数据的第N+3~N+M+2行，每行分别描述一个询问，其中第N+i+2行为两个由大小写字母组成的字符串Name1_i, Name2_i，分别表示小Hi询问中的两个名字。 对于100%的数据，满足N<=10^2，M<=10^2, 且数据中所有涉及的人物中不存在两个名字相同的人（即姓名唯一的确定了一个人）。 输出 对于每组测试数据，对于每个小Hi的询问，输出一行，表示查询的结果：如果根据已知信息，可以判定询问中的两个人存在共同的祖先，则输出他们的所有共同祖先中辈分最低的一个人的名字，否则输出-1。 样例输入 11 JiaYan JiaDaihua JiaDaihua JiaFu JiaDaihua JiaJing JiaJing JiaZhen JiaZhen JiaRong JiaYuan JiaDaishan JiaDaishan JiaShe JiaDaishan JiaZheng JiaShe JiaLian JiaZheng JiaZhu JiaZheng JiaBaoyu 3 JiaBaoyu JiaLian JiaBaoyu JiaZheng JiaBaoyu LinDaiyu 样例输出 JiaDaishan JiaZheng -1
最近公共祖先问题：给定一个家谱图，问某两个人的最近的公共祖先是谁，如果没有公共祖先，输出-1。最简单的方法题目提示得很清楚了：
当然你也先将一个人的祖先全都标记出来，然后顺着另一个的父亲一直向上找，直到找到第一个被标记过的结点，便是它们的最近公共祖先结点了。所以我就简单粗暴的使用STL的MAP和SET来解决问题了。假设需要判断的两个人名分别为son1和son2，那么①首先把*son1*及其所有祖先都找到并加入到一个set中，然后②首先判断son2在不在前面的set中，③如果不在，再依次判断son2的祖先在不在set中。 这里需要注意几点： 1. son1的祖先包括son1本身，比如第二个样例中的JiaBaoyu和JiaZheng，JiaZheng的祖先就包括JiaZheng自己，所以需要上面的第①和②步。 2. 为什么使用set而不是vector呢？因为②③步需要在son1的祖先中搜索，set内部用红黑树实现，搜索的效率高于vector。 知道了以上几点，就可以很快的写出代码了，完整代码如下： [cpp] #include<iostream> #include<map> #include<string> #include <set> using namespace std; int main() { //freopen("input.txt","r",stdin); int n,t; cin>>n; string son,father; map<string,string> son_father;//map[son]=father for(int i=0;i<n;i++) { cin>>father>>son; son_father.insert(make_pair(son,father)); } cin>>t; string son1,son2,comm_father; while(t–) { comm_father=""; cin>>son1>>son2; //vector<string> grand_fathers; set<string> grand_fathers;//使用set的查找效率高于vector grand_fathers.insert(son1);//注意，son1,son2本身也是一个祖先，一定要加进去，否则错！ while(son_father.find(son1)!=son_father.end()) { grand_fathers.insert(son_father[son1]); son1=son_father[son1]; } if(grand_fathers.find(son2)!=grand_fathers.end())//首先son2本身也是一个祖先，所以先判断一下//使用set的查找效率高于vector { if(t!=0) cout<<son2<<endl; else cout<<son2; continue; } while(son_father.find(son2)!=son_father.end()) { if(grand_fathers.find(son_father[son2])!=grand_fathers.end()) { comm_father=son_father[son2];//因为是son2从下往上找，所以第一个出下的肯定是最近的公共祖先 break; } else son2=son_father[son2]; } if(t!=0) { if(comm_father=="") cout<<"-1"<<endl; else cout<<comm_father<<endl; } else { if(comm_father=="") cout<<"-1"; else cout<<comm_father; } } return 0; } [/cpp] 本代码提交AC，用时4MS，内存0MB。 之前说了，我这种解法是非常简单粗暴的，事实上最近公共祖先问题是一个经典问题，有很多经典算法可以解决，我后面会进一步研究。]]>
现在我们分析红色那组字符，首先s[0]==s[2]不成立，可以把s[0]改成A；也可以把s[2]改成C，如果我们把s[2]改成C的话，虽然s[0]==s[2]成立，但是s[2]==s[4]又不成立了，又要修改s[4]；但是如果我们把s[0]改成A的话，则s[0]==s[2]==s[4]都成立，且修改次数更少。那么要怎样才能使修改的次数最少呢？
我们回到问题的本源：使用红色那组字符都相同，为了使修改次数最少，我们当然是将所有字符统一成当前出现次数最多的那个字符咯，这样只需要修改较少的非同一字符，在这个例子中，就是修改成出现次数最多的A。
如果前k个字符串和后k个字符串没有重叠，那就很简单了，只需依次检查对应字符是否相等。
理解了以上内容，代码很快就能写出来了：
[cpp]
#include<iostream>
#include<string>
using namespace std;
//求4个数的最大值
int max4(int a,int b,int c,int d)
{
int maxab=a>b?a:b;
int maxcd=c>d?c:d;
return maxab>maxcd?maxab:maxcd;
}
int main()
{
int t,k,n,d,ans;//t,k为题意；n为字符串长度；d为n-k相隔为d的字符需要相等；ans表示需要修改的碱基数量。
string s;
cin>>t;
while(t–)
{
ans=0;
cin>>s>>k;
n=s.size();
d=n-k;
if(2*k<=n)//如果最前k个碱基和最后k个碱基没有重叠的话
{
for(int i=0;i<k;i++)
if(s[i]!=s[i+d])//只需要依次检查对应字符是否相等即可
ans++;
}
else//如果有重叠，则另行讨论
{
for(int i=0;i<d;i++)//把所有碱基分成d组，需要确保每组都是同一个字符
{
int A=0,T=0,G=0,C=0,num=0;
for(int j=i;j<n;j+=d)//对于每一组，求出该组中出现次数最多的碱基的个数
{
num++;
if(s[j]==’A’)
A++;
else if(s[j]==’T’)
T++;
else if(s[j]==’G’)
G++;
else
C++;
}
int maxATGC=max4(A,T,G,C);//该组全部修改成出现次数最多的碱基
int change_num=num-maxATGC;//用该组中所有碱基个数减去出现次数最多的碱基个数，就是需要修改的碱基个数
ans+=change_num;
}
}
cout<<ans<<endl;
}
return 0;
}
[/cpp]
本代码提交AC，用时1MS，内存0MB。
]]>
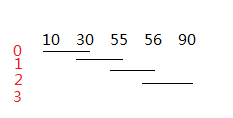左边的红色数字表示不同方案标号，这个标号也正好是该方案中数组a中的第一个插空位置的下标。很容易得到总的方案数有n-m+1个，所以我们只需将i从0到n-m+1循环枚举每一种方案，求最长的连续提交天数。
对于某一种方案，如上所述，其插空的开始下标正好为i，因为要插m个空，所以结束下标为m+i-1。那么这两者之间总的连续提交天数怎么算呢？比如上图中的方案2，如果把第55和56天填上，那么实际的连续提交天数应该是从31~89.也就是要从i-1对应的那天的后一天（31）算起，到m+i-1-1对应的那天的前一天（89）结束，总共就是89-31+1，也就是a[m+i-1+1]-a[i-1]-1；如果遇到最后一个空，因为m+i-1+1可能超过数组a的范围，所以我们添加一个a[n]=101，俗称哨兵；如果i==0的话，没有i-1，所以分开讨论。
最终的代码如下：
[cpp]
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int t;
cin>>t;
int n,m;
while(t–)
{
cin>>n>>m;
vector<int> a(n+1);
for(int i=0;i<n;i++)
cin>>a[i];
a[n]=101;//哨兵
if(m>=n)
cout<<100<<endl;
else
{
int max_days=0;//最长连续提交天数
int case_num=n-m+1;//总的枚举情况数
for(int i=0;i<case_num;i++)
{
int last_index=m+i-1;//该方案下最后一个下标
if(i==0)
{
if(a[last_index+1]-1>max_days)
max_days=a[last_index+1]-1;
}
else
{
if(a[last_index+1]-a[i-1]-1>max_days)
max_days=a[last_index+1]-a[i-1]-1;
}
}
cout<<max_days<<endl;
}
}
return 0;
}
[/cpp]
本代码提交AC，用时0MS，内存0MB。
]]>
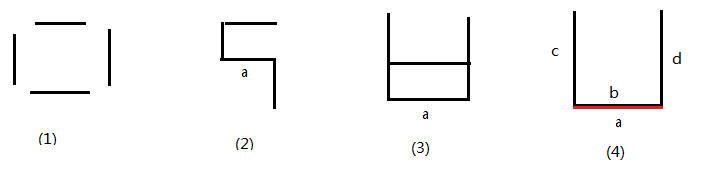要判断给出的点是否只有4个点，第一反应是用set集合，只要把题目给出的8个点都加入到set中，判断集合大小是否是4就可以了。
首先给出点的定义：
[cpp]
//点结构体
typedef struct P
{
int x,y;//两点坐标
bool operator<(const P& p)const//如果要加入到set中，需要重载<
{
//return this->x<p.x&&this->y<p.y;//注意这样会导致(0,0)<(0,1)且(0,1)<(0,0)的情况
return (this->x<p.x)||((this->x==p.x)&&(this->y<p.y));
}
bool operator==(const P&p)const//重载等于比较
{
return (this->x==p.x)&&(this->y==p.y);
}
};
[/cpp]
需要注意一点，因为需要把P加入到set中，而set是通过红黑树来排序的，所以需要重载小于<操作符。我最开始重载函数是这样写的
[cpp]
return this->x<p.x&&this->y<p.y;
[/cpp]
但是这样会有问题，如果给出两个点(0,0)和(0,1)，会得出(0,0)<(0,1)和(0,1)<(0,0)都不成立的结论，也就是说无法给(0,0)和(0,1)排序，也就无法插入到set中，所以需要修改成
[cpp]
return (this->x<p.x)||((this->x==p.x)&&(this->y<p.y));
[/cpp]
这样就能判断(0,0)<(0,1)成立了。有关这个问题可以参考
i的对称点i’下标为9，P[i’]=1，它的回文串没有超出以C为中心的回文串，根据对称性，则P[i]=P[i’]=1.
5. 第二种情况是，如果i=15，则P[15]等于多少呢？
由图可知，i的对称点i’=7，P[i’]=7，即以i’为中心的回文串已经超出了以C为中心的回文串，L左边的红色线条即为超出部分。那么此时不能说P[i]=P[i’]=7，因为如果这样的话，那么以C为中心的回文串也可以扩展到红色线条部分，这样P[C]就大于原来的P[C]了。但是可以肯定的是，i的半径至少是R-i=5，所以我们可以在此基础上依次增加i的半径，判断是否还是回文串。
6. 总结一下就是：