POJ 2251-Dungeon Master Dungeon Master Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 16959 Accepted: 6603 Description You are trapped in a 3D dungeon and need to find the quickest way out! The dungeon is composed of unit cubes which may or may not be filled with rock. It takes one minute to move one unit north, south, east, west, up or down. You cannot move diagonally and the maze is surrounded by solid rock on all sides. Is an escape possible? If yes, how long will it take? Input The input consists of a number of dungeons. Each dungeon description starts with a line containing three integers L, R and C (all limited to 30 in size). L is the number of levels making up the dungeon. R and C are the number of rows and columns making up the plan of each level. Then there will follow L blocks of R lines each containing C characters. Each character describes one cell of the dungeon. A cell full of rock is indicated by a ‘#’ and empty cells are represented by a ‘.’. Your starting position is indicated by ‘S’ and the exit by the letter ‘E’. There’s a single blank line after each level. Input is terminated by three zeroes for L, R and C. Output Each maze generates one line of output. If it is possible to reach the exit, print a line of the form Escaped in x minute(s). where x is replaced by the shortest time it takes to escape. If it is not possible to escape, print the line Trapped! Sample Input 3 4 5 S…. .###. .##.. ###.# ##### ##### ##.## ##… ##### ##### #.### ####E 1 3 3 S## #E# ### 0 0 0 Sample Output Escaped in 11 minute(s). Trapped! Source Ulm Local 1997
经典广度优先搜索题,网上居然把这题分到深度优先搜索了,害的我写好DFS提交后得到个TLE。 首先分析题意,给出一个立体的迷宫,要求从S走到E,求最短距离,其中迷宫中#不能走,.这个能走。我们可以用三维数组char dungeon[MAX_SIZE][MAX_SIZE][MAX_SIZE];来存储迷宫,对于某一个点dungeon[i][j][k],可以试探下面六个点:dungeon[i-1][j][k]、dungeon[i+1][j][k]、dungeon[i][j-1][k]、dungeon[i][j+1][k]、dungeon[i][j][k-1]、dungeon[i][j][k+1],想象你站在空间某一点,你可以往上、下、前、后、左、右走。 如果是深度搜索,试探到某点可行之后,访问它,并以该点为基点继续试探下去,直到到达E点或者无路可走,然后清除访问,每次到达E点,就比较一下这次走过的距离和上次的距离哪个小,当所有点都试探完毕时,就能得到最小值。 如果是广度搜索,以S点为起点,找到所有可行的下一个点,访问他们,并把他们插入到一个队列,然后在队列不为空的情况下循环:取出队首元素,以该元素为基点,找到所有可行的下一个点,访问他们,并把他们加入到队列中。如果广度搜索的过程中遇到E点,则此时走过的距离就是最小值,因为是广度搜索,最先访问到的肯定是最小值,不需要像深度搜索那样再进行比较。 下面是完整代码: [cpp] #include<iostream> #include<queue> using namespace std; const int MAX_SIZE=60; const int MAX_DISTANCE=1024; int L,R,C; char dungeon[MAX_SIZE][MAX_SIZE][MAX_SIZE];//迷宫 //int visited[MAX_SIZE][MAX_SIZE][MAX_SIZE]; int ans; int s_l,s_r,s_c,e_l,e_r,e_c; typedef struct P//点 { int x,y,z;//坐标 int dist;//从S到该点走过的距离 }; //深度搜索,结果正确,但是TLE /*void dfs(int l,int r,int c,int steps) { int visited[MAX_SIZE][MAX_SIZE][MAX_SIZE]={0};//每次初始化 if(l==e_l&&r==e_r&&c==e_c)//搜索成功 { if(steps<ans)//求最小值 ans=steps; return; } //深度搜索的六种情况 if((l-1)>=0&&visited[l-1][r][c]==0&&dungeon[l-1][r][c]==’.’) { visited[l-1][r][c]=1; dfs(l-1,r,c,steps+1);//继续深度搜索 visited[l-1][r][c]=0;//回溯 } if((l+1)<L&&visited[l+1][r][c]==0&&dungeon[l+1][r][c]==’.’) { visited[l+1][r][c]=1; dfs(l+1,r,c,steps+1); visited[l+1][r][c]=0; } if((r-1)>=0&&visited[l][r-1][c]==0&&dungeon[l][r-1][c]==’.’) { visited[l][r-1][c]=1; dfs(l,r-1,c,steps+1); visited[l][r-1][c]=0; } if((r+1)<R&&visited[l][r+1][c]==0&&dungeon[l][r+1][c]==’.’) { visited[l][r+1][c]=1; dfs(l,r+1,c,steps+1); visited[l][r+1][c]=0; } if((c-1)>=0&&visited[l][r][c-1]==0&&dungeon[l][r][c-1]==’.’) { visited[l][r][c-1]=1; dfs(l,r,c-1,steps+1); visited[l][r][c-1]=0; } if((c+1)<C&&visited[l][r][c+1]==0&&dungeon[l][r][c+1]==’.’) { visited[l][r][c+1]=1; dfs(l,r,c+1,steps+1); visited[l][r][c+1]=0; } }*/ //广度搜索 bool bfs(int s_l,int s_r,int s_c) { int visited[MAX_SIZE][MAX_SIZE][MAX_SIZE]={0};//记得每次都要初始化为0,否则会影响下一个case queue<P> P_Q;//队列 P p,next_p; p.x=s_l,p.y=s_r,p.z=s_c,p.dist=0; visited[s_l][s_r][s_c]=1; P_Q.push(p); int l,r,c; while(!P_Q.empty()) { p=P_Q.front(); P_Q.pop(); if(p.x==e_l&&p.y==e_r&&p.z==e_c) { ans=p.dist;//因为是广度搜索,最先到达E,肯定就是最小值 return true; } l=p.x,r=p.y,c=p.z; //广度搜索的六种情况 if((l-1)>=0&&visited[l-1][r][c]==0&&dungeon[l-1][r][c]==’.’) { visited[l-1][r][c]=1; next_p.x=l-1; next_p.y=r; next_p.z=c; next_p.dist=p.dist+1; P_Q.push(next_p); } if((l+1)<L&&visited[l+1][r][c]==0&&dungeon[l+1][r][c]==’.’) { visited[l+1][r][c]=1; next_p.x=l+1; next_p.y=r; next_p.z=c; next_p.dist=p.dist+1; P_Q.push(next_p); } if((r-1)>=0&&visited[l][r-1][c]==0&&dungeon[l][r-1][c]==’.’) { visited[l][r-1][c]=1; next_p.x=l; next_p.y=r-1; next_p.z=c; next_p.dist=p.dist+1; P_Q.push(next_p); } if((r+1)<R&&visited[l][r+1][c]==0&&dungeon[l][r+1][c]==’.’) { visited[l][r+1][c]=1; next_p.x=l; next_p.y=r+1; next_p.z=c; next_p.dist=p.dist+1; P_Q.push(next_p); } if((c-1)>=0&&visited[l][r][c-1]==0&&dungeon[l][r][c-1]==’.’) { visited[l][r][c-1]=1; next_p.x=l; next_p.y=r; next_p.z=c-1; next_p.dist=p.dist+1; P_Q.push(next_p); } if((c+1)<C&&visited[l][r][c+1]==0&&dungeon[l][r][c+1]==’.’) { visited[l][r][c+1]=1; next_p.x=l; next_p.y=r; next_p.z=c+1; next_p.dist=p.dist+1; P_Q.push(next_p); } } return false; } int main() { //freopen("input.txt","r",stdin); while(cin>>L>>R>>C&&L&&R&&C) { ans=MAX_DISTANCE; for(int i=0;i<L;i++) for(int j=0;j<R;j++) for(int k=0;k<C;k++) { cin>>dungeon[i][j][k]; if(dungeon[i][j][k]==’S’) { s_l=i; s_r=j; s_c=k; } else if(dungeon[i][j][k]==’E’) { dungeon[i][j][k]=’.’;//注意这里改成了’.’,便于BFS里搜索判断 e_l=i; e_r=j; e_c=k; } } //dfs(s_l,s_r,s_c,0); if(bfs(s_l,s_r,s_c)) cout<<"Escaped in "<<ans<<" minute(s)."<<endl; else cout<<"Trapped!"<<endl; } return 0; } [/cpp] 本代码提交AC,用时63MS,内存1248K。]]>
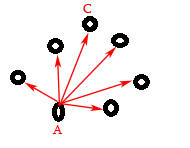
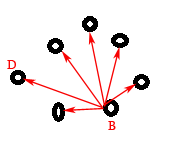 假设分别从A点和B点开始的单源最短距离如上两张图所示,那么Stockbroker从A点开始传播谣言总共需要多长时间呢?因为传播是可以同时进行的,所以传播结束时间就是A点到其他点中的最长距离,也就是上图中的AC。同理,如果从B点开始,则|BD|是传播时间。
综上所述,本题的求解过程可以归纳为以下几步:
1. 测试图中的每一个点$$i$$,求从该点出发,到其他所有点的单源最短距离集合$$S_i$$
2. 求出该单源最短距离$$S_i$$内部的最大值$$M_i$$
3. 对于图中的所有点,求其$$M_i$$
4. 最后求所有$$M_i$$中的最小值$$MIN$$,即为最终结果
所以根据上面的步骤,我们可以用n次Dijkstra算法求每个点的单源最短距离内部的最大值$$M_i$$,然后求$$MIN$$。其实也可以不用这么麻烦,因为我们还有另外一个更简单的算法Floyd算法。使用Floyd算法求得所有点对的最短距离,自然就知道某个点的单源最短距离了。
在写代码的时候还有一些小问题需要注意,对于数据输入,请仔细多读几遍Input说明,如果还是有困难,请看
假设分别从A点和B点开始的单源最短距离如上两张图所示,那么Stockbroker从A点开始传播谣言总共需要多长时间呢?因为传播是可以同时进行的,所以传播结束时间就是A点到其他点中的最长距离,也就是上图中的AC。同理,如果从B点开始,则|BD|是传播时间。
综上所述,本题的求解过程可以归纳为以下几步:
1. 测试图中的每一个点$$i$$,求从该点出发,到其他所有点的单源最短距离集合$$S_i$$
2. 求出该单源最短距离$$S_i$$内部的最大值$$M_i$$
3. 对于图中的所有点,求其$$M_i$$
4. 最后求所有$$M_i$$中的最小值$$MIN$$,即为最终结果
所以根据上面的步骤,我们可以用n次Dijkstra算法求每个点的单源最短距离内部的最大值$$M_i$$,然后求$$MIN$$。其实也可以不用这么麻烦,因为我们还有另外一个更简单的算法Floyd算法。使用Floyd算法求得所有点对的最短距离,自然就知道某个点的单源最短距离了。
在写代码的时候还有一些小问题需要注意,对于数据输入,请仔细多读几遍Input说明,如果还是有困难,请看