918. Maximum Sum Circular Subarray
Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.
Here, a circular array means the end of the array connects to the beginning of the array. (Formally, C[i] = A[i] when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)
Also, a subarray may only include each element of the fixed buffer A at most once. (Formally, for a subarray C[i], C[i+1], ..., C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)
Example 1:
Input: [1,-2,3,-2] Output: 3 Explanation: Subarray [3] has maximum sum 3
Example 2:
Input: [5,-3,5] Output: 10 Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10
Example 3:
Input: [3,-1,2,-1] Output: 4 Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4
Example 4:
Input: [3,-2,2,-3] Output: 3 Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3
Example 5:
Input: [-2,-3,-1] Output: -1 Explanation: Subarray [-1] has maximum sum -1
Note:
-30000 <= A[i] <= 300001 <= A.length <= 30000
给定一个循环数组,即数组的最后一个和数字第一个连起来了。求循环数组的最大连续子数组和。
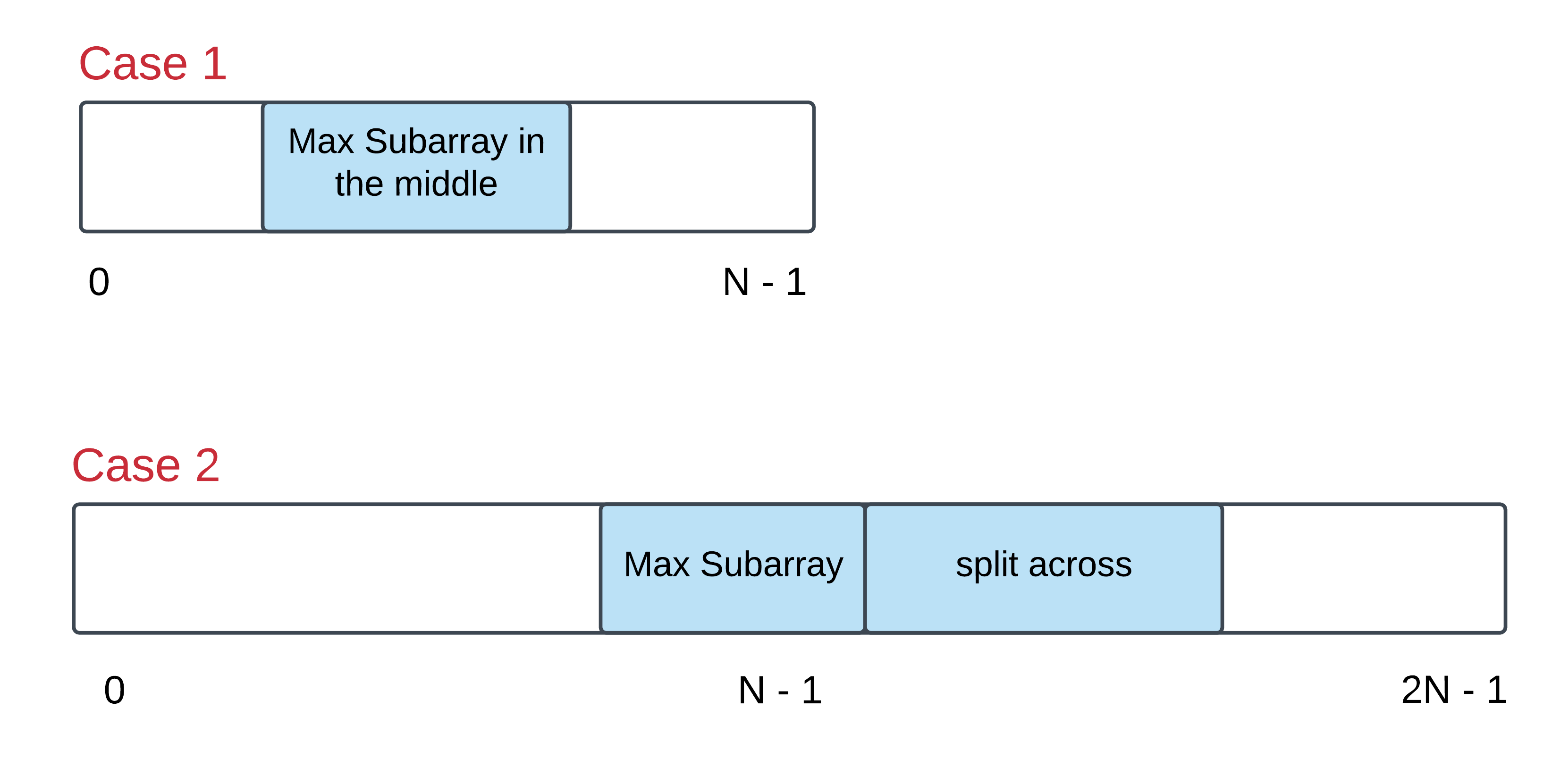
LeetCode Maximum Subarray的升级版,即数组首尾相连了。我一开始想到的解法是,既然数组首尾相连了,那就2*n次dp即可,即把原数组复制一遍,接到原数组后面,形成2*n长的数组,然后照样跑原来的DP算法。这个解法是不对的,比如如果数组是[1,2,3,4]这种全是正数,则跑2n遍之后,ans会一直max更新,导致最后的ans是1+…+4+1+…4,即数组加了两遍,每个数重复加了。另外对于数组[5,-3,5]这种,也会完整数组加两遍。
正确解法是,分两种情况,第一种情况是最大子串和没有跨越首尾,则使用常规DP即可求解。第二种情况是,最大子串和跨越了首尾,则可以把问题转化为求原数组的最小连续子串和,然后用数组总和减去最小连续子串和,就能得到跨越首尾的最大连续子串和。在求解第二种情况时,需要注意如果最小连续子串和是整个数组的情况,比如数组都是负数[-1,-2,-3],则求到的最小连续子串和是整个数组[-1,-2,-3],用数组总和一减变成了空集和为0,但最大连续子串和至少需要1个元素,对于这种情况,丢弃case2的解。
完整代码如下:
class Solution {
public:
int maxSubarraySumCircular(vector<int>& A) {
int n = A.size();
vector<int> dp(n, 0);
// 最大连续子串
dp[0] = A[0];
int ans1 = A[0], sum = A[0];
for(int i = 1; i < n; ++i) {
dp[i] = max(dp[i - 1], 0) + A[i];
ans1 = max(ans1, dp[i]);
sum += A[i];
}
// 最小连续子串
fill(dp.begin(), dp.end(), 0);
dp[0] = A[0];
int ans2 = A[0];
for(int i = 1; i < n; ++i) {
dp[i] = min(dp[i - 1], 0) + A[i];
ans2 = min(ans2, dp[i]);
}
if(ans2 == sum) ans2 = INT_MIN; // 注意最小连续子串和不能是全长数组
else ans2 = sum - ans2;
return max(ans1, ans2);
}
};本代码提交AC,用时252MS。