LeetCode Range Addition II Given an m * n matrix M initialized with all 0‘s and several update operations. Operations are represented by a 2D array, and each operation is represented by an array with two positive integers a and b, which means M[i][j] should be added by one for all 0 <= i < a and 0 <= j < b. You need to count and return the number of maximum integers in the matrix after performing all the operations. Example 1:
Input: m = 3, n = 3 operations = [[2,2],[3,3]] Output: 4 Explanation: Initially, M = [[0, 0, 0], [0, 0, 0], [0, 0, 0]] After performing [2,2], M = [[1, 1, 0], [1, 1, 0], [0, 0, 0]] After performing [3,3], M = [[2, 2, 1], [2, 2, 1], [1, 1, 1]] So the maximum integer in M is 2, and there are four of it in M. So return 4.Note:
- The range of m and n is [1,40000].
- The range of a is [1,m], and the range of b is [1,n].
- The range of operations size won’t exceed 10,000.
给定一个全为0的矩阵M，和一系列的操作，每个操作都是一对(a,b)，表示要对所有i在[0,a)和j在[0,b)的元素M[i][j]，问最终矩阵M中最大元素的个数。 这个题稍微想一下就会发现非常简单。 假设矩阵的左下角坐标为(0,0)，对于某一个操作(a,b)，表示把以(0,0)和(a,b)为对角顶点的子矩阵元素加1。那么(a1,b1)和(a2,b2)两个操作的重叠区域(0,0)-(a2,b1)所在子矩阵的元素就被加了两次，他们的值最大且相同。
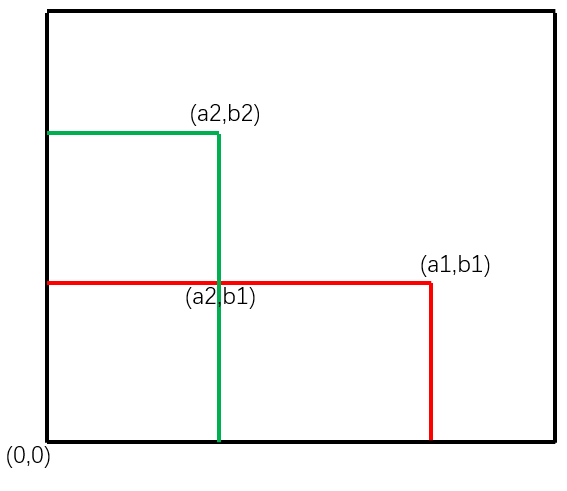所以我们只需要遍历所有操作，分别找到行和列的最小值，则他们和原点围成的子矩阵的元素值最大，且相等。
代码非常简单，如下：
[cpp]
class Solution {
public:
int maxCount(int m, int n, vector<vector<int>>& ops) {
int minRow = m, minCol = n;
for (const auto &op : ops) {
minRow = min(minRow, op[0]);
minCol = min(minCol, op[1]);
}
return minRow*minCol;
}
};
[/cpp]
本代码提交AC，用时6MS。
]]>
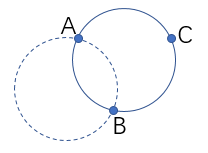已知两点求圆心的方法请看
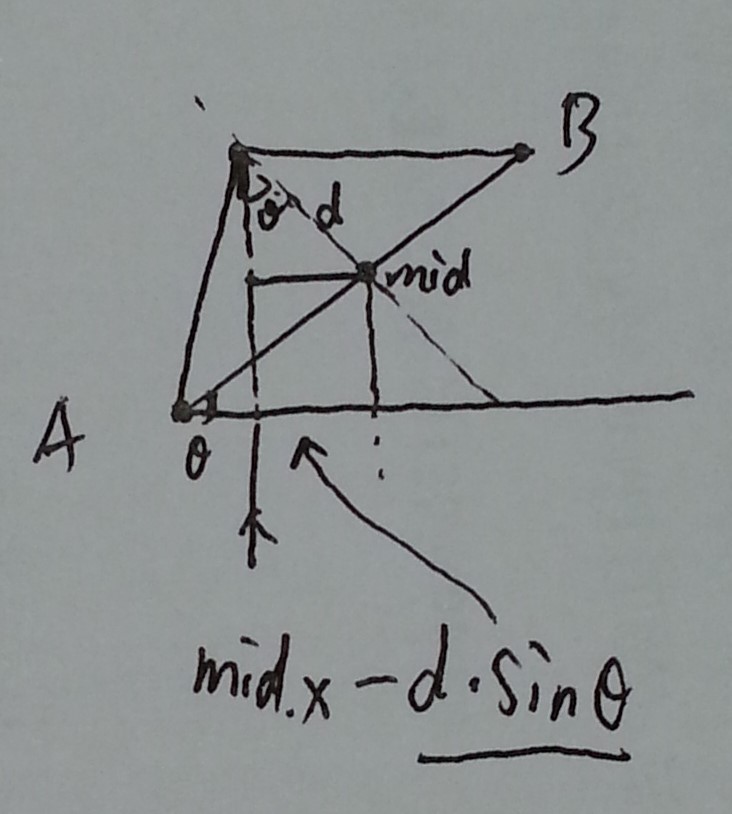暴力方法在hiho上TLE，需要寻求更高效的算法。
假设以两个点i,j为圆心画半径为R的圆，如果两个圆相交，则在相交的弧上任意一点画圆，都能覆盖原来的i,j两点。基于这个思想，假设现在固定点i为圆心，R为半径画圆，求出所有以其他点为圆心画的圆和圆i相交的弧，则在相交重叠次数最多的那段弧上的点为圆心画的圆肯定能覆盖最多的点，覆盖的点数就是这段弧被重叠的次数。每个点i都能求出这样一个最大值，则所有点的这个最大值的最大值就是全局能覆盖的最多点。
怎样表示两个圆相交的那段弧呢，使用极坐标，因为弧是由两条半径张成的，所以可以表示成两条半径的极坐标夹角，并且标明夹角的开始（is=1）和结束（is=-1）。求重叠次数最多的弧的方法是，把所有重叠弧的起止半径的极坐标夹角排个序，然后遍历一下，当夹角开始（is=1）次数最多且结束（is=-1）次数最少时，说明重叠次数最多，所以就是is的累加和的最大值。
完整代码借鉴