Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example:
Input: [1,8,6,2,5,4,8,3,7] Output: 49
题意是x轴上立着一堆线段，从这些线段中找两根和x轴构成一个木桶，问哪个木桶能装最多的水。 暴力枚举的话，是$O(n^2)$的。我们可以用贪心的思路来解决：要使木桶装更多的水，短板越长越好，且两根线之间的距离越长也越好。 设置首尾指针i,j，计算由i,j夹到的木桶的体积（这里简单点，面积即可），如果height[i]<height[j]，则i++，因为短板越长越好，所以这相当于抛弃了height[i]，保留height[j]，底板减1。
完整代码如下：
class Solution {
public:
int maxArea(vector<int>& height)
{
int mA = 0, i = 0, j = height.size() – 1;
while (i != j) {
int cur = min(height[i], height[j]) * (j – i);
if (cur > mA)
mA = cur;
if (height[i] < height[j])
i++;
else
j--;
}
return mA;
}
};本代码提交AC，用时24MS。
二刷。
证明贪心方法的正确性一般用反证法，推出矛盾即可，证明过程见讨论区：https://discuss.leetcode.com/topic/503/anyone-who-has-a-o-n-algorithm。
三刷。反证法过程：刚开始的时候l=0,r=n-1，假设此时height[l]<height[r]，则此时的组合对l来说是它能形成最大面积的情况。因为x轴长度最大，当r往左边走的时候，x肯定会变小；如果r往左走遇到比l更短的y，则总的y变短，面积变小；如果r往左走遇到比l更长的y，则依然是l作为y，但因为x已经变小了，所以面积依然变小。总之，每一次组合，都是对更短的那个柱子的最大面积，而更长的柱子还有可能和其他柱子组成更大的面积，所以我们每次丢掉短柱子，保留长柱子。
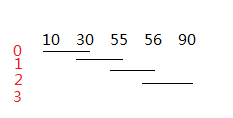左边的红色数字表示不同方案标号，这个标号也正好是该方案中数组a中的第一个插空位置的下标。很容易得到总的方案数有n-m+1个，所以我们只需将i从0到n-m+1循环枚举每一种方案，求最长的连续提交天数。
对于某一种方案，如上所述，其插空的开始下标正好为i，因为要插m个空，所以结束下标为m+i-1。那么这两者之间总的连续提交天数怎么算呢？比如上图中的方案2，如果把第55和56天填上，那么实际的连续提交天数应该是从31~89.也就是要从i-1对应的那天的后一天（31）算起，到m+i-1-1对应的那天的前一天（89）结束，总共就是89-31+1，也就是a[m+i-1+1]-a[i-1]-1；如果遇到最后一个空，因为m+i-1+1可能超过数组a的范围，所以我们添加一个a[n]=101，俗称哨兵；如果i==0的话，没有i-1，所以分开讨论。
最终的代码如下：
[cpp]
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int t;
cin>>t;
int n,m;
while(t–)
{
cin>>n>>m;
vector<int> a(n+1);
for(int i=0;i<n;i++)
cin>>a[i];
a[n]=101;//哨兵
if(m>=n)
cout<<100<<endl;
else
{
int max_days=0;//最长连续提交天数
int case_num=n-m+1;//总的枚举情况数
for(int i=0;i<case_num;i++)
{
int last_index=m+i-1;//该方案下最后一个下标
if(i==0)
{
if(a[last_index+1]-1>max_days)
max_days=a[last_index+1]-1;
}
else
{
if(a[last_index+1]-a[i-1]-1>max_days)
max_days=a[last_index+1]-a[i-1]-1;
}
}
cout<<max_days<<endl;
}
}
return 0;
}
[/cpp]
本代码提交AC，用时0MS，内存0MB。
]]>