写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：
F(0) = 0, F(1) = 1
F(N) = F(N – 1) + F(N – 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。
示例 1：
输入：n = 2
输出：1
示例 2：
输入：n = 5
输出：5
提示：
0 <= n <= 100
注意：本题与主站 509 题相同：https://leetcode-cn.com/problems/fibonacci-number/
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/fei-bo-na-qi-shu-lie-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
求斐波那契数列的第n项。看之前的POJ题解： http://code.bitjoy.net/2017/05/04/poj-3070-fibonacci/ 。
一共有三种解法。常规解法就是无脑递归调用。关键是如何分析这种解法的时空复杂度。无脑调用是F(n)=F(n-1)+F(n-2)。想象一下，递归调用二叉树（ https://wmjtxt.github.io/2018/12/26/three_method_of_fibonacci/ ）。每个节点都会分裂出2个孩子，然后孩子继续2倍分裂，所以总调用次数大概是$O(2^n)$，这是时间复杂度。空间复杂度就是递归调用的栈深度，就是树的高度，大概是$O(n)$。
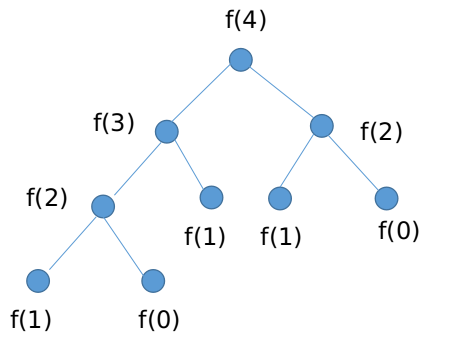
常规解法是，DP的思路，每次保留数列前两项，然后不断更新这两个数。时间复杂度是$O(n)$，空间复杂度是O(1)。完整代码如下：
class Solution {
public:
int fib(int n) {
if(n == 0) return 0;
if(n == 1) return 1;
long long a = 0, b = 1;
for(int i = 2; i <= n; ++i) {
long long tmp = a + b;
tmp %= 1000000007;
a = b;
b = tmp;
}
return b;
}
};本代码提交AC，用时0MS。
最优的解法是矩阵快速幂的方法，求矩阵[[1,1],[1,0]]的n次幂，然后矩阵逆对角线位置的值就是F(n)的值。快速幂可以做到$O(lg(n))$的时间复杂度，完整代码如下：
typedef long long LL;
class Solution {
private:
vector<vector<LL>> multiply(vector<vector<LL>> &m1, vector<vector<LL>> &m2) {
int n = m1.size();
vector<vector<LL>> ans(n, vector<LL>(n, 0));
for(int i = 0; i < n; ++i) {
for(int j = 0; j < n; ++j) {
for(int k = 0; k < n; ++k) {
ans[i][j] += m1[i][k] * m2[k][j] % 1000000007;
}
}
}
return ans;
}
public:
int fib(int n) {
if(n == 0) return 0;
if(n == 1) return 1;
vector<vector<LL>> matrix = {{1,1},{1,0}};
vector<vector<LL>> ans = {{1,0},{0,1}};
while(n != 0) {
if(n % 2 == 1) ans = multiply(ans, matrix);
matrix = multiply(matrix, matrix);
n >>= 1;
}
return ans[0][1] % 1000000007;
}
};本代码提交AC，用时4MS。
