Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example:
Consider the following matrix:
[ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ]
Given target = 5, return true.
Given target = 20, return false.
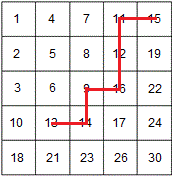
在LeetCode Search a 2D Matrix基础上改动了一点点，但是难度增加不少。这一次，每行和每列都是递增的，但是这一行的行首元素和上一行的行末元素没有大小关系，这种矩阵有点像从左上角递增到右下角的一个曲面，想象一下。 一种比较笨的办法就是对每一行或者每一列二分搜索，复杂度为O(mlgn)或O(nlgm)。 参考这位大神的介绍，有很多厉害的算法，具体看原博客，这里简单给出其前两个算法的C++实现。 算法1相当于对角二分搜索，是线性复杂度的。搜索从矩阵右上角开始，遇到比当前元素大时，递增行；遇到比当前元素小时，递减列；直到找到相等元素，或者到达矩阵左下角。最坏情况是从右上角走到了左下角，复杂度为O(m+n)。 这种思路的代码如下：
class Solution {
public:
bool searchMatrix(vector<vector<int> >& matrix, int target)
{
if (matrix.size() == 0)
return false;
int m = matrix.size(), n = matrix[0].size();
if (n == 0)
return false;
int i = 0, j = n – 1;
while (i < m && j >= 0) {
while (i < m && matrix[i][j] < target)
++i;
if (i >= m)
return false;
while (j >= 0 && matrix[i][j] > target)
–j;
if (j < 0)
return false;
if (matrix[i][j] == target)
return true;
}
return false;
}
};
本代码提交AC，用时129MS。
算法2利用了分治法的思路。每次取矩阵中心元素，把矩阵分成4个小份。如果target大于中心元素，则左上角部分可以全部舍弃掉，因为矩阵的行列都是递增的，左上角元素肯定全部小于中心元素，不必再找。此时可以递归的在剩余的3个小矩阵里查找。比如下图中心元素为9，如果要找26，则可以递归的在其右上角、左下角和右下角三个小矩阵中查找。
时间复杂度公式为T(n)=3T(n/2)+c，c为target和中心元素比较的时间。使用主方法可以算到T(n)=O(n1.58)。
分治法思路代码如下：
class Solution {
public:
bool quadPart(vector<vector<int> >& matrix, int left, int top, int right, int bottom, int target)
{
if (left > right || top > bottom)
return false;
if (target < matrix[left][top] || target > matrix[right][bottom])
return false;
int midrow = left + (right - left) / 2, midcol = top + (bottom - top) / 2;
if (target == matrix[midrow][midcol])
return true;
//if (target > matrix[midrow][midcol]) { // 抛弃左上角
// return quadPart(matrix, left, midcol + 1, midrow - 1, bottom, target) || // 右上角
// quadPart(matrix, midrow + 1, top, right, midcol - 1, target) || // 左下角
// quadPart(matrix, midrow, midcol, right, bottom, target); // 右下角
//}
//else {
// return quadPart(matrix, left, midcol + 1, midrow - 1, bottom, target) || // 右上角
// quadPart(matrix, midrow + 1, top, right, midcol - 1, target) || // 左下角
// quadPart(matrix, left, top, midrow, midcol, target); //左上角
//}
if (target > matrix[midrow][midcol]) { // 抛弃左上角
return quadPart(matrix, left, midcol + 1, midrow, bottom, target) || // 右上角
quadPart(matrix, midrow + 1, top, right, midcol, target) || // 左下角
quadPart(matrix, midrow + 1, midcol + 1, right, bottom, target); // 右下角
}
else {
return quadPart(matrix, left, midcol, midrow - 1, bottom, target) || // 右上角
quadPart(matrix, midrow, top, right, midcol - 1, target) || // 左下角
quadPart(matrix, left, top, midrow - 1, midcol - 1, target); //左上角
}
}
bool searchMatrix(vector<vector<int> >& matrix, int target)
{
if (matrix.size() == 0)
return false;
int m = matrix.size(), n = matrix[0].size();
if (n == 0)
return false;
return quadPart(matrix, 0, 0, m - 1, n - 1, target);
}
};本代码提交AC，用时168MS。
注意代码中注释掉的部分是错误代码，因为其在右下角或者左上角搜索时可能会进入死循环。比如要在上图搜索30，当搜索到右下角深色部分的小矩阵时，中心元素是17，本该搜索更小的矩阵30，但是根据注释代码中第一个if搜索右下角的代码，新的矩阵（右下角）的左上角坐标还是17，因为其坐标是(midrow, midcol)，无论递归多少次，右下角的矩阵没有变小，所以进入了死循环。
正确的方法是把涉及到中点的两条边分配到不同的小矩阵里，必须使得每个小矩阵的左上角或右下角坐标有变化。
完整代码如下：
[cpp]
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if (root == NULL)return "";
string ans = to_string(root->val);
if (root->left) ans += ","+serialize(root->left);
if (root->right) ans += ","+serialize(root->right);
return ans;
}
void insert(TreeNode* root, TreeNode* node) {
if (node->val < root->val) {
if (root->left == NULL)root->left = node;
else insert(root->left, node);
}
else {
if (root->right == NULL)root->right = node;
else insert(root->right, node);
}
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if (data == "")return NULL;
TreeNode* root = NULL;
for (int start = 0, end = 0; end <= data.size(); ++end) {
if (data[end] == ‘,’ || end == data.size()) {
TreeNode* node = new TreeNode(atoi(data.substr(start, end – start).c_str()));
if (root == NULL)root = node;
else insert(root, node);
start = end + 1;
}
}
return root;
}
};
[/cpp]
本代码提交AC，用时26MS。]]>
