输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
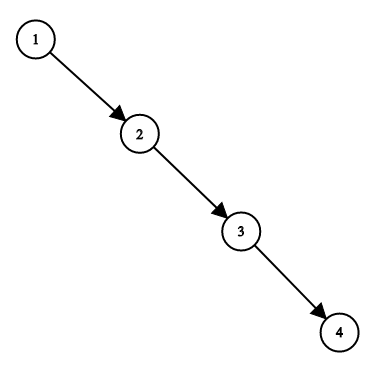
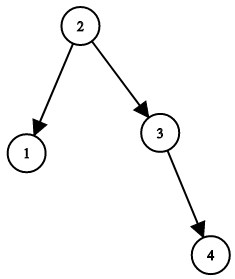
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
注意:本题与主站 426 题相同:https://leetcode-cn.com/problems/convert-binary-search-tree-to-sorted-doubly-linked-list/
注意:此题对比原题有改动。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
如何将二叉搜索树转换in-place转换为有序双向链表。
此题同时考察了多个知识点,首先二叉搜索树转换为有序结果,需要使用二叉树的中序遍历,然后要in-place转换为双向链表,则需要在遍历二叉树的过程中,对每个节点,修改其left和right指针,使其分别指向转换后的双向链表的前驱和后继节点。
使用递归的方法,设置两个全局变量pre和head,分别表示当前遍历节点的前驱节点,以及转换后的双向链表的头结点。完整代码如下:
class Solution {
private:
Node *pre, *head;
void DFS(Node *root) {
if(root == NULL) return;
DFS(root->left);
if(head == NULL) head = root;
else pre->right = root;
root->left = pre;
pre = root;
DFS(root->right);
}
public:
Node* treeToDoublyList(Node* root) {
if(root == NULL) return NULL;
pre = head = NULL;
DFS(root);
head->left = pre;
pre->right = head;
return head;
}
};本代码提交AC,用时12MS。