5474. Number of Good Leaf Nodes Pairs
Given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.
Return the number of good leaf node pairs in the tree.
Example 1:
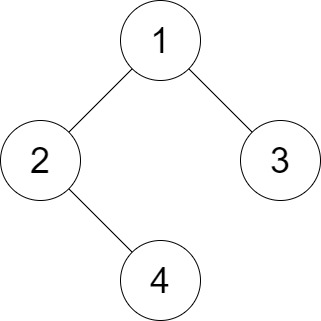
Input: root = [1,2,3,null,4], distance = 3 Output: 1 Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
Example 2:
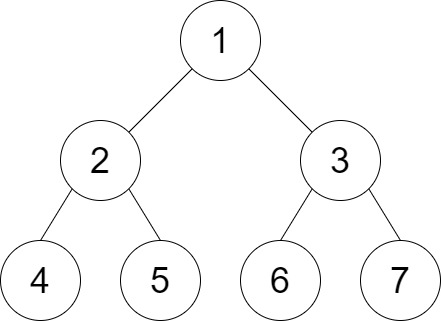
Input: root = [1,2,3,4,5,6,7], distance = 3 Output: 2 Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.
Example 3:
Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3 Output: 1 Explanation: The only good pair is [2,5].
Example 4:
Input: root = [100], distance = 1 Output: 0
Example 5:
Input: root = [1,1,1], distance = 2 Output: 1
Constraints:
- The number of nodes in the
treeis in the range[1, 2^10]. - Each node’s value is between
[1, 100]. 1 <= distance <= 10
这一题第一眼看上去还是有难度的，后来观察数据量，发现总节点数才1024，则叶子节点数会更少，所以首先尝试了暴力方法。
暴力方法分为两个阶段，第一阶段是找到所有的叶子节点，第二阶段是求任意两个叶子节点的最短距离。
第一阶段在递归查找所有叶子节点时，保留了从根到该叶子的路径，以便后续求任意两个叶子的距离。第二阶段求距离时，思路比较简单，比如第一个样例，节点4的路径是1-2-4，节点3的路径是1-3，则两条路径都从根节点开始，看看两者的最长的公共前缀，直到找到它们的最后一个公共节点，相当于它们的最近公共祖先，然后假设最近公共祖先为两个叶子的子树的根节点，算两个叶子的高度，高度相加就是它们的最短距离。完整代码如下：
class Solution {
private:
void CollectLeaves(TreeNode *root, unordered_map<TreeNode*, vector<TreeNode*>> &all_paths, vector<TreeNode*> &one_path) {
if (root == NULL)return;
one_path.push_back(root);
if (root->left == NULL && root->right == NULL) {
all_paths[root] = one_path;
}
else {
CollectLeaves(root->left, all_paths, one_path);
CollectLeaves(root->right, all_paths, one_path);
}
one_path.pop_back();
}
int CalDist(vector<TreeNode*> &path1, vector<TreeNode*> &path2) {
int m = path1.size(), n = path2.size();
int i = 0;
while (i < m&&i < n) {
if (path1[i] != path2[i])break;
++i;
}
return (m - i) + (n - i);
}
public:
int countPairs(TreeNode* root, int distance) {
unordered_map<TreeNode*, vector<TreeNode*>> all_paths;
vector<TreeNode*> one_path;
CollectLeaves(root, all_paths, one_path);
vector<TreeNode*> leaves;
for (unordered_map<TreeNode*, vector<TreeNode*>>::iterator it = all_paths.begin(); it != all_paths.end(); ++it) {
leaves.push_back(it->first);
}
int ans = 0;
for (int i = 0; i < leaves.size(); ++i) {
for (int j = i + 1; j < leaves.size(); ++j) {
int d = CalDist(all_paths[leaves[i]], all_paths[leaves[j]]);
if (d <= distance)++ans;
}
}
return ans;
}
};本代码提交AC。
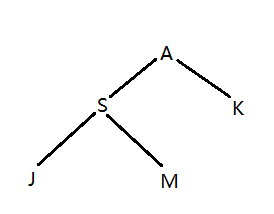是样例输入构成的一个家谱树，我们常规DFS这个树的序列是这样的：ASJMK。但是本题在进入和离开某个节点时都需要记录下来，而且每访问完一个子节点，要访问下一个子节点时，也需要记录当前父节点。比如访问完J准备访问M时，需要记录S，由此形成的序列为：ASJSMSAKA。
DFS生成的数组B长度大概为边数的两倍，所以复杂度级别只是O(n)的。
DFS之后就把树转换为了数组B[]，因为使用RMQ-ST算法需要求某个区间的最小深度节点，所以在DFS的时候还需要记录每个节点的深度信息，而且还要记录每个节点最后访问的下标，这两点都不难，大家直接看代码即可。
RMQ-ST算法
得到数组B后就好办了，可以利用昨天学习的RMQ-ST算法求解2的幂区间长度间深度最小的节点，不过因为我们这题最终输出的是节点的名字而不是节点的深度，所以RMQ-ST比较的是深度，但存储的是节点名。
观察RMQ-ST算法的二重循环知道其复杂度为O(nlgn)。
在线求解
一切准备就绪后就可以求解了，首先根据字符串名字找到对应数字序号，然后查看两节点最后出现在树中的下标l,r，再讲[l,r]区间分成能覆盖[l,r]的2的幂的长度的半区间[l,t]和[t+1,r]，最后求这两个区间最小深度的节点，输出其名称。
完整代码如下：
[cpp]
#include<iostream>
#include<map>
#include<string>
#include<vector>
#include<cmath>
using namespace std;
const int MAX_N=100010;//最大人数
map<string,int> name_index;//名字转换为数字
vector<string> index_name(MAX_N);//数字转换为名字
int n,m,k;//k全部记录将树转换成数组tree[]是的下标，转换结束时k即为tree[]的长度
vector<vector<int> > f_s(MAX_N);//f_s[i]表示第i个父亲的所有孩子
int tree[2*MAX_N];//DFS将树转换为的数组
int depth[MAX_N];//每个点在树中的深度
int rmq[MAX_N][30];//区间深度最低值
int last_show[MAX_N];//某个元素最后出现在tree中的位置（下标）
//保存某个人的信息，并返回其下标
int store_name(string name)
{
map<string,int>::iterator it=name_index.find(name);
if(it==name_index.end())//还不存在
{
int curr_index=name_index.size();//用当前已有人数作为其下标，正好是递增的。
name_index.insert(make_pair(name,curr_index));
index_name[curr_index]=name;//记录
return curr_index;//返回下标
}
else
return it->second;//已经存在，直接返回
}
//深度遍历树
void DFS(int root,int deep)
{
tree[k++]=root;//进入即记录
depth[root]=deep;//记录深度
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
DFS(f_s[root][i],deep+1);
tree[k++]=root;//每返回一次都要记录一次根节点
}
last_show[root]=k-1;//root节点最后出现的位置
}
//求a,b最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
void init_rmq()
{
for(int j=0;j<k;j++)
//rmq[j][0]=depth[tree[j]];
rmq[j][0]=tree[j];//保存的是这个节点，而不是它的深度，方便最后输出
int q=floor(log((double)k)/log(2.0));
for(int i=1;i<=q;i++)
{
for(int j=k-1;j>=0;j–)
{
rmq[j][i]=rmq[j][i-1];
if(j+(1<<(i-1))<k)
{
if(depth[rmq[j+(1<<(i-1))][i-1]]<depth[rmq[j][i]])//+优先级高于<<，所以改j+1<<(i-1)为j+(1<<(i-1))
rmq[j][i]=rmq[j+(1<<(i-1))][i-1];
}
//rmq[j][i]=get_min(rmq[j][i],rmq[j+1<<(i-1)][i-1]);
}
}
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
string name1,name2;
int index1,index2;
while(n–)
{
cin>>name1>>name2;
index1=store_name(name1);
index2=store_name(name2);
f_s[index1].push_back(index2);
}
k=0;//开始时树的下标为0，DFS完之后正好是tree[]数组的长度，可以作为rmq-st的n
DFS(0,0);
init_rmq();
cin>>m;
int l,r,t;
while(m–)
{
cin>>name1>>name2;
if(name1==name2)
{
cout<<name1<<endl;
continue;
}
index1=store_name(name1);
index2=store_name(name2);
l=last_show[index1];
r=last_show[index2];
if(l>r)//保证l<=r
{
int tmp=r;
r=l;
l=tmp;
}
t=floor(log(double(r-l+1))/log(2.0));//找到能使[l,r]分为两半的指数
cout<<index_name[get_min(rmq[l][t],rmq[r-(1<<t)+1][t])]<<endl;//r-(1<<t)+1，记得+1
}
return 0;
}
[/cpp]
本代码提交AC，用时202MS，内存8MB。
相比于
In the figure, each node is labeled with an integer from {1, 2,…,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,…, N. Each of the next N -1 lines contains a pair of integers that represent an edge –the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N – 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
Source
Taejon 2002