hihoCoder 1093-最短路径·三：SPFA算法 #1093 : 最短路径·三：SPFA算法 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 万圣节的晚上，小Hi和小Ho在吃过晚饭之后，来到了一个巨大的鬼屋！ 鬼屋中一共有N个地点，分别编号为1..N，这N个地点之间互相有一些道路连通，两个地点之间可能有多条道路连通，但是并不存在一条两端都是同一个地点的道路。 不过这个鬼屋虽然很大，但是其中的道路并不算多，所以小Hi还是希望能够知道从入口到出口的最短距离是多少？ 提示：Super Programming Festival Algorithm。 输入 每个测试点（输入文件）有且仅有一组测试数据。 在一组测试数据中： 第1行为4个整数N、M、S、T，分别表示鬼屋中地点的个数和道路的条数，入口（也是一个地点）的编号，出口（同样也是一个地点）的编号。 接下来的M行，每行描述一条道路：其中的第i行为三个整数u_i, v_i, length_i，表明在编号为u_i的地点和编号为v_i的地点之间有一条长度为length_i的道路。 对于100%的数据，满足N<=10^5，M<=10^6, 1 <= length_i <= 10^3, 1 <= S, T <= N, 且S不等于T。 对于100%的数据，满足小Hi和小Ho总是有办法从入口通过地图上标注出来的道路到达出口。 输出 对于每组测试数据，输出一个整数Ans，表示那么小Hi和小Ho为了走出鬼屋至少要走的路程。 样例输入 5 10 3 5 1 2 997 2 3 505 3 4 118 4 5 54 3 5 480 3 4 796 5 2 794 2 5 146 5 4 604 2 5 63 样例输出 172
对于边稀疏的图，SPFA算法可以更高效的求解单源最短路径问题。 假设要求S和T的最短路径，该算法使用一个队列，最开始队列中只有(S,0)—表示当前处于点S，从点S到达该点的距离为0，然后每次从队首取出一个节点(i, L)——表示当前处于点i，从点S到达该点的距离为L，接下来遍历所有从这个节点出发的边(i, j, l)——表示i和j之间有一条长度为l的边，在将(j, L+l)加入到队列之前，先判断队列中是否存在点j，如果存在(j,l’)，则比较L+l和l’的大小关系，如果L+l>=l’，那么(j,L+l)这条路就没必要继续搜索下去了，所以不将(j,L+l)加入队列；如果L+l<l’，那么原来的(j,l’)没必要继续搜索下去了，把(j,l’)替换成(j,L+l)即可。如果原队列中不存在j点，则直接把(j,L+l)加入队列。 当队列为空时，(T,ans)就是S到T的距离为ans。所以SPFA在某种程度上来说，就是BFS+剪枝。 SPFA的原理不难，写代码的时候要注意几点：1）N的范围是N<=10^5，如果用数组存储的话，内存够呛，所以建议用vector动态分配；2）每次从队列中弹出一个点时，记得将其在队列中的标记清空，即used[i]=0；3）处理好数据结构问题，因为数据输入中2点之间的距离可能有多个值，你可以在输入的时候只存储最小值，你也可以为了方便先把所有数据都存起来，统一在SPFA算法中进行大小判断，本代码使用第二种策略。
完整代码如下：
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
const int MAX_N = 1e5 + 10;
const int INF = 1e6 + 10;
int n, m, s, t;
//int path[MAX_N][MAX_N];//数组太大，改用vector动态分配
vector<int> path[MAX_N]; //path[i][j]表示第i个点和第path[i][j]个点有路相同，其中j是输入的顺序
vector<int> dist[MAX_N]; //dist[i][j]表示和第i个点相连的第j个点的距离是dist[i][j]，path[i][j]和dist[i][j]是通过相同的j来共享数据
int used[MAX_N]; //used[i]表示第i个点是否在队列中
int s_dist[MAX_N]; //s_dist[i]表示第i个点和起始点s的距离
int spfa()
{
int q1 = s;
used[q1] = 1;
for (int i = 1; i <= n; i++)
s_dist[i] = INF;
s_dist[s] = 0;
queue<int> Q;
Q.push(q1);
while (!Q.empty()) {
q1 = Q.front();
Q.pop();
used[q1] = 0; //当弹出队列时记得设置used[i]=0
int qs = path[q1].size(); //和q1点相连的点的个数
for (int i = 0; i < qs; i++) {
int u = path[q1][i];
if (s_dist[q1] + dist[q1][i] < s_dist[u]) //如果u是q1的父节点，肯定不满足这一条，所以不会回溯
{
s_dist[u] = s_dist[q1] + dist[q1][i];
if (used[u] == 0) {
used[u] = 1;
Q.push(u);
}
}
}
}
return s_dist[t];
}
int main()
{
//freopen("input.txt","r",stdin);
scanf("%d%d%d%d", &n, &m, &s, &t);
int u, v, len;
while (m–) {
scanf("%d%d%d", &u, &v, &len); //记录了所有数据，此处还可以优化
path[u].push_back(v);
path[v].push_back(u);
dist[u].push_back(len);
dist[v].push_back(len);
}
printf("%d\n", spfa());
return 0;
}本代码提交AC，用时208MS，内存19MB。
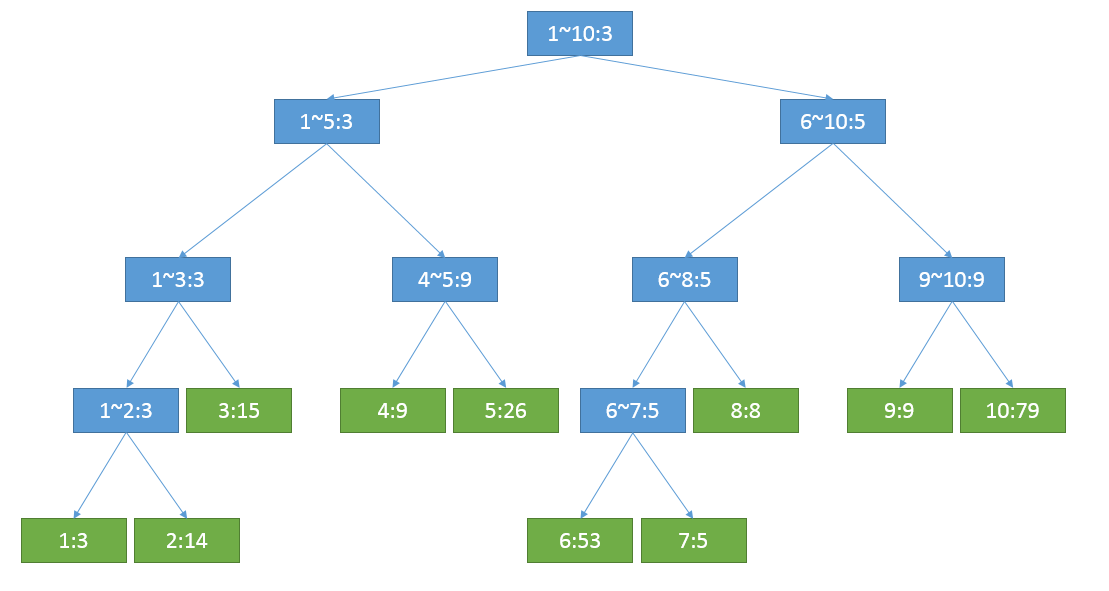上图是线段树的一个例子，每个节点保存了区间范围以及该区间的最小值。总的区间大小是[1,10]，仔细看看这个区间树的节点个数只有19个；另外再画一个[1,6]区间上的区间树，节点个数只有11个。可以不加证明的得出一个n的区间长度的线段树的节点个数为2*n-1，这远远小于n*n，所以我们只需要O(n)的空间来存储，而不是O(n^2)。
反观之前
设利用扩展欧几里得算法求到的式(3)的解为$$k_0$$和$$t_0$$，那么式(2)的解为$$k=(b/d)k_0$$，$$t=(b/d)t_0$$。那么最小的k是多少呢？
又因为根据数论中的
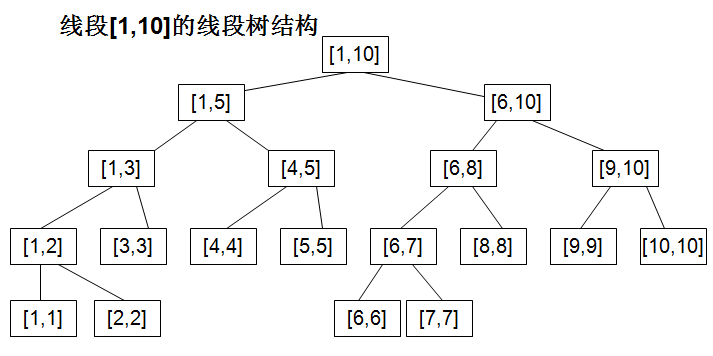从图中可以看到构造线段树的过程就是一个二分的过程，不断将区间分成两半，直到只有一个元素。图中的线段树每一个节点是一个区间[l,r]，本题我稍微改造了一下，改成了数组int seg_tree[left][length]，比如seg_tree[i][j]表示从下标i开始，长度为j的这样一个区间上的最小值，这样就可以利用线段树来解决RMQ问题了。比如改造后的线段树就成了下面的样子：
因为树形这种特殊的结构，我们可以用一个DFS来对树实现二分构造，当DFS到某个节点长度为1时，其最小值就是w[i]本身，在回溯到父节点时，父节那个区间的最小值又是所有子节点最小值中的最小值。因为树的总节点数大约为2*n，所以复杂度O(n)。
当需要查询区间[l,r]的最小值时，只需对数组seg_tree二分搜索。具体来说，假设我们搜索到了节点[s_l,s_len]，如果r<(s_l+s_len/2)，说明区间[l,r]全在[s_l,s_len]的左边，我们递归在[s_l,s_len/2]区间找；如果l>=(s_l+s_len/2)，说明区间[l,r]全在[s_l,s_len]的右边，我们递归在[s_l+s_len/2,s_len-s_len/2]区间找；如果以上两者都不是，说明[l,r]跨界了，而且中点下标一定是s_l+s_len/2，所以我们分别在二两半区间找，然后求这两者的最小值。复杂度O(lgn)。
当需要更新某个下标为pos的值为value时，也是DFS查找线段树，直到找到叶子seg_tree[pos][1]，更新它的值，以及所有我们在查找过程经过的父节点的值。复杂度O(lgn)。
所以线段是的性质使得无论是构造、查询、更新操作，复杂度都只要O(lgn)，这就是题目中所说的把总的复杂度平均分配到不同操作：平衡乃和谐之理。
完整代码如下：
[cpp]
#include<iostream>
using namespace std;
const int MAX_N=1e4+2;
int w[MAX_N];//每个商品重量
int n,m;
int seg_tree[MAX_N][MAX_N];//seg_tree[i][j]：起点为i，长度为j的区间的最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
//深度优先遍历以构造线段树
void dfs(int left,int length)
{
if(length==1)
{
seg_tree[left][1]=w[left];
return;
}
dfs(left,length/2);
dfs(left+length/2,length-length/2);
seg_tree[left][length]=get_min(seg_tree[left][length/2],seg_tree[left+length/2][length-length/2]);//取最小值
}
//在区间[s_left,s_len]搜索区间[left,length]的最小值
int search_min(int s_left,int s_len,int left,int length)
{
if((s_left==left)&&(s_len==length))
return seg_tree[s_left][s_len];
if((left+length-1)<(s_left+s_len/2))//全在左半部分
{
return search_min(s_left,s_len/2,left,length);
}
else if(left>=(s_left+s_len/2))//全在右半部分
{
return search_min(s_left+s_len/2,s_len-s_len/2,left,length);
}
else//左右分开搜索
{
int left_len=s_left+s_len/2-left;
int right_len=length-left_len;
int min_left=search_min(s_left,s_len/2,left,left_len);
int min_right=search_min(s_left+s_len/2,s_len-s_len/2,s_left+s_len/2,right_len);
return get_min(min_left,min_right);
}
}
//从区间[s_left,s_len]开始更新下标pos的值为value
void update(int s_left,int s_len,int pos,int value)
{
if((s_left==pos)&&(s_len==1))
{
seg_tree[s_left][1]=value;
return ;
}
int mid=s_left+s_len/2;
if(pos<mid)
update(s_left,s_len/2,pos,value);
else
update(mid,s_len-s_len/2,pos,value);
seg_tree[s_left][s_len]=get_min(seg_tree[s_left][s_len/2],seg_tree[mid][s_len-s_len/2]);//更新父节点
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
for(int i=1;i<=n;i++)
cin>>w[i];
dfs(1,n);
cin>>m;
int p,l,r;
for(int i=0;i<m;i++)
{
cin>>p>>l>>r;
if(p==0)//查询
{
cout<<search_min(1,n,l,r-l+1)<<endl;
}
else//修改
{
update(1,n,l,r);
}
}
return 0;
}
[/cpp]
本代码提交AC，用时151MS，内存42MB。
]]>
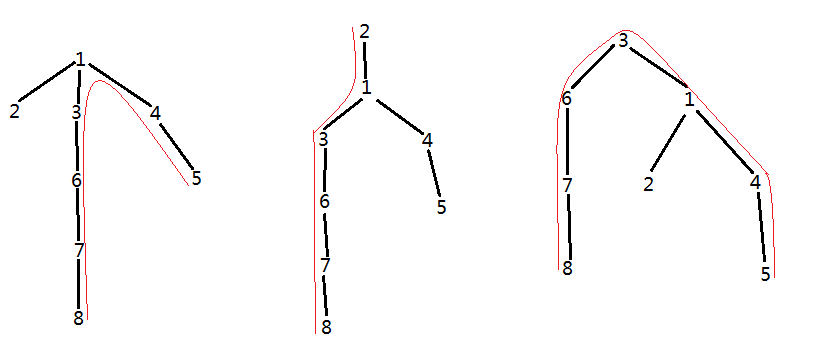因为我们默认以t为根的树的最长路径一定经过节点t，所以上图最长路径分别为图中红色路线所示，长度分别为6,5,6（因为节点1和3都在最长路径上，所以他们求得的最长路径相等）。同理我们还可以求出以4,5…n为根（路径转折点）的最长路径，最后求这些最长路径中的最大值。
这个版本的代码如下：
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int MAX_N=1e5+2;
int n;//节点数
vector<vector<int> > f_s(MAX_N);//father-son和son-father关系，存储双边
vector<int> first,second;//first[i]和second[i]分别表示以i节点为根节点时（i节点以下构成的子树）的最大和次大长度
//参数分别为当前节点，父亲节点
void dfs(int root,int father)
{
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
if(f_s[root][i]!=father)//不能回溯
{
dfs(f_s[root][i],root);
if(first[f_s[root][i]]+1>first[root])
{
second[root]=first[root];
first[root]=first[f_s[root][i]]+1;
}
else if(first[f_s[root][i]]+1>second[root])
second[root]=first[f_s[root][i]]+1;
}
}
}
void init_first_second()
{
first.clear();
first.assign(n+1,0);
second.clear();
second.assign(n+1,0);
}
int main()
{
freopen("input.txt","r",stdin);
cin>>n;
int a,b;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
f_s[a].push_back(b);//记录双边关系
f_s[b].push_back(a);//记录双边关系
}
int ans=0;
for(int i=1;i<=n;i++)//枚举每一个节点为根节点（转折点）
{
init_first_second();
dfs(i,-1);
if(first[i]+second[i]>ans)
ans=first[i]+second[i];
}
cout<<ans;
return 0;
}
[/cpp]
但是很遗憾，提交后TLE。
后来我仔细想了想，无论我们从哪个点s开始对树DFS，我们求得的first[i]和second[i]都是以点i为根构成的子树中它的最长和次长距离，那么first[i]+second[i]不就代表了从i开始DFS时得到的最长距离吗？比如图中以2为根的树中，我们在DFS的过程中肯定已经求到了first[1]和second[1]，然后才能求first[2]和second[2]，而这里的first[1]和second[2]和图中以1为根时求得的first[1]和second[1]是完全一样的。而对于以3为根的树，因为3正好在最长路径上，所以这里的first[1]和second[1]要小于前面两种情况，但是first[3]+second[3]和前面两种情况的first[1]+second[1]是相等的。
说了这么多，不知道同学们有没有发现，不管从哪个点开始DFS，只要一遍DFS结束，最长路径总会出现在某个first[i]+second[i]中。
至此，可以省略上一个版本中的for循环，只要一个DFS即可：
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int MAX_N=1e5+2;
int n;//节点数
vector<vector<int> > f_s(MAX_N);//father-son和son-father关系，存储双边
vector<int> first,second;//first[i]和second[i]分别表示以i节点为根节点时（i节点以下构成的子树）的最大和次大长度
int longest=0;//最终结果
//参数分别为当前节点，父亲节点
void dfs(int root,int father)
{
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
if(f_s[root][i]!=father)//不能回溯
{
dfs(f_s[root][i],root);
if(first[f_s[root][i]]+1>first[root])//更新最大和次大
{
second[root]=first[root];
first[root]=first[f_s[root][i]]+1;
}
else if(first[f_s[root][i]]+1>second[root])//只更新次大
second[root]=first[f_s[root][i]]+1;
}
}
if(first[root]+second[root]>longest)//更新全局最大
longest=first[root]+second[root];
}
void init_first_second()
{
first.assign(n+1,0);
second.assign(n+1,0);
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
int a,b;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
f_s[a].push_back(b);//记录双边关系
f_s[b].push_back(a);//记录双边关系
}
init_first_second();
dfs(1,-1);//使用任意一个节点DFS，结果都是一样的。
/*int ans=0;
for(int i=1;i<=n;i++)//该循环可在DFS时完成
{
if(first[i]+second[i]>ans)
ans=first[i]+second[i];
}*/
cout<<longest;
return 0;
}
[/cpp]
本代码提交AC，用时224MS，内存9MB。
第二种方法不太好理解，所以还是建议大家用第一种方法。
网上关于树的直径介绍了3种方法，可以参考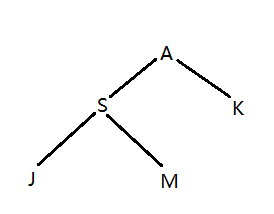
是样例输入构成的一个家谱树，我们常规DFS这个树的序列是这样的：ASJMK。但是本题在进入和离开某个节点时都需要记录下来，而且每访问完一个子节点，要访问下一个子节点时，也需要记录当前父节点。比如访问完J准备访问M时，需要记录S，由此形成的序列为：ASJSMSAKA。
DFS生成的数组B长度大概为边数的两倍，所以复杂度级别只是O(n)的。
DFS之后就把树转换为了数组B[]，因为使用RMQ-ST算法需要求某个区间的最小深度节点，所以在DFS的时候还需要记录每个节点的深度信息，而且还要记录每个节点最后访问的下标，这两点都不难，大家直接看代码即可。
RMQ-ST算法
得到数组B后就好办了，可以利用昨天学习的RMQ-ST算法求解2的幂区间长度间深度最小的节点，不过因为我们这题最终输出的是节点的名字而不是节点的深度，所以RMQ-ST比较的是深度，但存储的是节点名。
观察RMQ-ST算法的二重循环知道其复杂度为O(nlgn)。
在线求解
一切准备就绪后就可以求解了，首先根据字符串名字找到对应数字序号，然后查看两节点最后出现在树中的下标l,r，再讲[l,r]区间分成能覆盖[l,r]的2的幂的长度的半区间[l,t]和[t+1,r]，最后求这两个区间最小深度的节点，输出其名称。
完整代码如下：
[cpp]
#include<iostream>
#include<map>
#include<string>
#include<vector>
#include<cmath>
using namespace std;
const int MAX_N=100010;//最大人数
map<string,int> name_index;//名字转换为数字
vector<string> index_name(MAX_N);//数字转换为名字
int n,m,k;//k全部记录将树转换成数组tree[]是的下标，转换结束时k即为tree[]的长度
vector<vector<int> > f_s(MAX_N);//f_s[i]表示第i个父亲的所有孩子
int tree[2*MAX_N];//DFS将树转换为的数组
int depth[MAX_N];//每个点在树中的深度
int rmq[MAX_N][30];//区间深度最低值
int last_show[MAX_N];//某个元素最后出现在tree中的位置（下标）
//保存某个人的信息，并返回其下标
int store_name(string name)
{
map<string,int>::iterator it=name_index.find(name);
if(it==name_index.end())//还不存在
{
int curr_index=name_index.size();//用当前已有人数作为其下标，正好是递增的。
name_index.insert(make_pair(name,curr_index));
index_name[curr_index]=name;//记录
return curr_index;//返回下标
}
else
return it->second;//已经存在，直接返回
}
//深度遍历树
void DFS(int root,int deep)
{
tree[k++]=root;//进入即记录
depth[root]=deep;//记录深度
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
DFS(f_s[root][i],deep+1);
tree[k++]=root;//每返回一次都要记录一次根节点
}
last_show[root]=k-1;//root节点最后出现的位置
}
//求a,b最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
void init_rmq()
{
for(int j=0;j<k;j++)
//rmq[j][0]=depth[tree[j]];
rmq[j][0]=tree[j];//保存的是这个节点，而不是它的深度，方便最后输出
int q=floor(log((double)k)/log(2.0));
for(int i=1;i<=q;i++)
{
for(int j=k-1;j>=0;j–)
{
rmq[j][i]=rmq[j][i-1];
if(j+(1<<(i-1))<k)
{
if(depth[rmq[j+(1<<(i-1))][i-1]]<depth[rmq[j][i]])//+优先级高于<<，所以改j+1<<(i-1)为j+(1<<(i-1))
rmq[j][i]=rmq[j+(1<<(i-1))][i-1];
}
//rmq[j][i]=get_min(rmq[j][i],rmq[j+1<<(i-1)][i-1]);
}
}
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
string name1,name2;
int index1,index2;
while(n–)
{
cin>>name1>>name2;
index1=store_name(name1);
index2=store_name(name2);
f_s[index1].push_back(index2);
}
k=0;//开始时树的下标为0，DFS完之后正好是tree[]数组的长度，可以作为rmq-st的n
DFS(0,0);
init_rmq();
cin>>m;
int l,r,t;
while(m–)
{
cin>>name1>>name2;
if(name1==name2)
{
cout<<name1<<endl;
continue;
}
index1=store_name(name1);
index2=store_name(name2);
l=last_show[index1];
r=last_show[index2];
if(l>r)//保证l<=r
{
int tmp=r;
r=l;
l=tmp;
}
t=floor(log(double(r-l+1))/log(2.0));//找到能使[l,r]分为两半的指数
cout<<index_name[get_min(rmq[l][t],rmq[r-(1<<t)+1][t])]<<endl;//r-(1<<t)+1，记得+1
}
return 0;
}
[/cpp]
本代码提交AC，用时202MS，内存8MB。
相比于
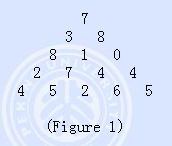Figure 1 shows a number triangle. Write a program that calculates the highest sum of numbers passed on a route that starts at the top and ends somewhere on the base. Each step can go either diagonally down to the left or diagonally down to the right.
Input
Your program is to read from standard input. The first line contains one integer N: the number of rows in the triangle. The following N lines describe the data of the triangle. The number of rows in the triangle is > 1 but <= 100. The numbers in the triangle, all integers, are between 0 and 99.
Output
Your program is to write to standard output. The highest sum is written as an integer.
Sample Input
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30
Source
IOI 1994