Quoit Design
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 77740 Accepted Submission(s): 20729
Problem DescriptionHave you ever played quoit in a playground? Quoit is a game in which flat rings are pitched at some toys, with all the toys encircled awarded.
In the field of Cyberground, the position of each toy is fixed, and the ring is carefully designed so it can only encircle one toy at a time. On the other hand, to make the game look more attractive, the ring is designed to have the largest radius. Given a configuration of the field, you are supposed to find the radius of such a ring.
Assume that all the toys are points on a plane. A point is encircled by the ring if the distance between the point and the center of the ring is strictly less than the radius of the ring. If two toys are placed at the same point, the radius of the ring is considered to be 0.
InputThe input consists of several test cases. For each case, the first line contains an integer N (2 <= N <= 100,000), the total number of toys in the field. Then N lines follow, each contains a pair of (x, y) which are the coordinates of a toy. The input is terminated by N = 0.
OutputFor each test case, print in one line the radius of the ring required by the Cyberground manager, accurate up to 2 decimal places.
Sample Input
2 0 0 1 1 2 1 1 1 1 3 -1.5 0 0 0 0 1.5 0
Sample Output
0.71 0.00 0.75
AuthorCHEN, Yue
SourceZJCPC2004
RecommendJGShining | We have carefully selected several similar problems for you: 10061009100510081004
给定二维平面上的N个点，问其中距离最近的两个点的距离是多少，输出最短距离的一半。
典型的平面上最近点对问题。大学算法课上有，采用分治法。即首先把所有点按x排序，然后取x轴中点m，把所有点划分为左右两半L和R，在L和R中递归求最近点对的距离，假设为dL和dR。假设d=min(dL,dR)。则还需要判断最近点对是否会在中点m附近，假设存在这种情况，则跨越m的最近点对必须满足距离m小于d。把这部分点收集起来，按y排序，然后求任意两点之间的距离，期间可以break加速。
完整代码如下：
#include<iostream>
#include<vector>
#include<algorithm>
#include<functional>
using namespace std;
struct Point
{
double x_, y_;
Point() :x_(0), y_(0) {};
Point(double x, double y) :x_(x), y_(y) {};
};
bool CmpX(const Point &p1, const Point &p2) {
return p1.x_ < p2.x_;
}
bool CmpY(const Point &p1, const Point &p2) {
return p1.y_ < p2.y_;
}
// 暂时只算距离平方，最后开平方根
double CalDist(const Point &p1, const Point &p2) {
return (p1.x_ - p2.x_)*(p1.x_ - p2.x_) + (p1.y_ - p2.y_)*(p1.y_ - p2.y_);
}
double CalMinDist(vector<Point> &data, int l, int r) {
if (r - l == 2) {
return CalDist(data[l], data[l + 1]);
}
else if (r - l == 3) {
double d1 = CalDist(data[l], data[l + 1]);
double d2 = CalDist(data[l], data[l + 2]);
double d3 = CalDist(data[l + 1], data[l + 2]);
return min(min(d1, d2), d3);
}
int m = l + (r - l) / 2;
int mx = data[m].x_;
double dd = min(CalMinDist(data, l, m), CalMinDist(data, m, r));
double d = sqrt(dd);
vector<Point> rect;
for (int i = l; i < r; ++i) {
if (data[i].x_ > mx - d && data[i].x_ < mx + d) {
rect.push_back(data[i]);
}
}
sort(rect.begin(), rect.end(), CmpY);
for (int i = 0; i < rect.size(); ++i) {
for (int j = i + 1; j < rect.size(); ++j) {
double tmpd = CalDist(rect[i], rect[j]);
if (tmpd > dd)break;
dd = min(dd, tmpd);
}
}
return dd;
}
int main() {
freopen("input.txt", "r", stdin);
int n;
while (scanf("%d", &n)) {
if (n == 0)break;
vector<Point> data(n, Point());
for (int i = 0; i < n; ++i) {
scanf("%lf %lf", &data[i].x_, &data[i].y_);
}
sort(data.begin(), data.end(), CmpX);
printf("%.2lf\n", sqrt(CalMinDist(data, 0, data.size())) / 2);
}
return 0;
}本代码提交AC，用时982MS。
参考： https://www.cnblogs.com/MartinLwx/p/9757828.html 、 https://www.jianshu.com/p/8bc681afbaff
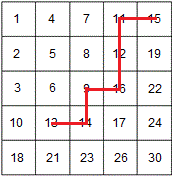
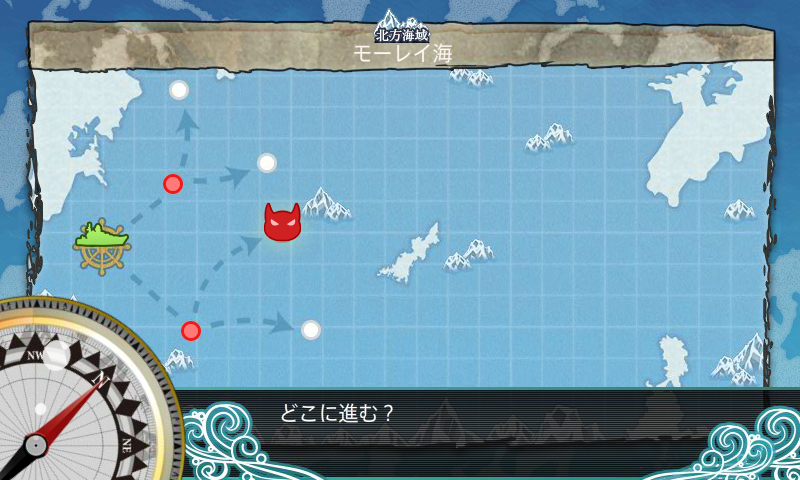其中红色的点表示有敌人驻扎，猫头像的的点表示该地图敌军主力舰队(boss)的驻扎点，虚线表示各个战略点之间的航线(无向边)。
在游戏中要从一个战略点到相邻战略点需要满足一定的条件，即需要舰队的索敌值大于等于这两点之间航线的索敌值需求。
由于提高索敌值需要将攻击机、轰炸机换成侦察机，舰队索敌值越高，也就意味着舰队的战力越低。
另外在每一个战略点会发生一次战斗，需要消耗1/K的燃料和子弹。必须在燃料和子弹未用完的情况下进入boss点才能与boss进行战斗，所以舰队最多只能走过K条航路。
现在Nettle想要以最高的战力来进攻boss点，所以他希望能够找出一条从起始点(编号为1的点)到boss点的航路，使得舰队需要达到的索敌值最低，并且有剩余的燃料和子弹。
特别说明：两个战略点之间可能不止一条航线，两个相邻战略点之间可能不止一条航线。保证至少存在一条路径能在燃料子弹用完前到达boss点。
提示：你在找什么？
输入
第1行：4个整数N,M,K,T。N表示战略点数量，M表示航线数量，K表示最多能经过的航路，T表示boss点编号, 1≤N,K≤10,000, N≤M≤100,000
第2..M+1行：3个整数u,v,w，表示战略点u,v之间存在航路，w表示该航路需求的索敌值，1≤w≤1,000,000。
输出
第1行：一个整数，表示舰队需要的最小索敌值。
样例输入
5 6 2 5
1 2 3
1 3 2
1 4 4
2 5 2
3 5 5
4 5 3
样例输出
3