POJ 2965-The Pilots Brothers’ refrigerator The Pilots Brothers’ refrigerator Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 19188 Accepted: 7358 Special Judge Description The game “The Pilots Brothers: following the stripy elephant” has a quest where a player needs to open a refrigerator. There are 16 handles on the refrigerator door. Every handle can be in one of two states: open or closed. The refrigerator is open only when all handles are open. The handles are represented as a matrix 4х4. You can change the state of a handle in any location [i, j] (1 ≤ i, j ≤ 4). However, this also changes states of all handles in row i and all handles in column j. The task is to determine the minimum number of handle switching necessary to open the refrigerator. Input The input contains four lines. Each of the four lines contains four characters describing the initial state of appropriate handles. A symbol “+” means that the handle is in closed state, whereas the symbol “−” means “open”. At least one of the handles is initially closed. Output The first line of the input contains N – the minimum number of switching. The rest N lines describe switching sequence. Each of the lines contains a row number and a column number of the matrix separated by one or more spaces. If there are several solutions, you may give any one of them. Sample Input -+– —- —- -+– Sample Output 6 1 1 1 3 1 4 4 1 4 3 4 4 Source Northeastern Europe 2004, Western Subregion
这一题和之前做的POJ Problem 1753: Flip Game大同小异，只是这题要求记录搜索路径，并且翻转的时候是同行同列的所有格子都翻转，对之前那题的代码稍作修改即可。 这一题要求翻转的时候是翻转和(i,j)点同行同列的所有点，我们还是通过异或来完成。比如我们要对 [cpp] -+– —- —- -+– [/cpp] 的(0,0)（坐标从0开始）及其行列翻转，应该怎么办呢？ 因为1^1=0,1^0=1，所以如果我们要改变某一位，只需要将该位异或1即可。又因为我们输入的时候是从左到右，从上到下的顺序，所以当我们要翻转第0行的时候，只需要异或0xf<<12，0xf<<12相当于把4个二进制1移到最左边（因为第0行在最左边），如果是翻转第i行，则异或0xf<<(4*(3-i))；当我们要翻转某一列时，因为同一列的二进制位相差3个位置，所以异或值的形式为二进制0001000100010001，又因为(i,j)这个位置在行翻转的时候已经翻转过了，所以在列翻转时不能再翻转了，否则回到原状态了，所以根据行号的不同，我们可以得到不同的列异或值，分别是curr_xor=0x111,0x1011,0x1101,0x1110，列翻转的公式是next_p.val^=curr_xor<<(3-j);。这个问题用笔在纸上演算一下就会很明白了。 还有一个问题是怎样来记录搜索的路径，我的办法是开辟两个数组： [cpp] typedef struct P//翻转时的格子坐标 { int x,y; }; P trace[MAX_STATUS];//trace[i]到达i状态值时翻转的某个格子坐标 int pre[MAX_STATUS];//pre[i]记录i状态的前一个状态值 [/cpp] pre[i]数组用来记录到达i状态时的前一个状态，而trace[i]则用来记录到达该状态时翻转的格子坐标。这样通过成功状态回溯到开始状态就可以找到所有路径了，具体实现请看下面的代码。 完整代码如下： [cpp] #include<iostream> #include<queue> #include<vector> using namespace std; const int MAX_STATUS=65536;//2^16=65536种，所以[0,65535] const int ALL_1=65535;//全1 int visited[MAX_STATUS]={0};//访问标记 int XOR[4]={0x111,0x1011,0x1101,0x1110};//列异或值 typedef struct POS//position翻转位置 { int val;//当前翻转状态的值 int step;//到当前状态共翻转了多少次 }; typedef struct P//翻转时的格子坐标 { int x,y; }; P trace[MAX_STATUS];//trace[i]到达i状态值时翻转的某个格子坐标 int pre[MAX_STATUS];//pre[i]记录i状态的前一个状态值 //通过反向索引打印结果 void print_result(POS pos,int init_id) { cout<<pos.step<<endl; vector<P> points; points.push_back(trace[pos.val]); int pre_val=pre[pos.val]; while(pre_val!=init_id)//当没有追溯到初始状态时，一直循环 { points.push_back(trace[pre_val]); pre_val=pre[pre_val];//追溯 } int p_num=points.size();//顺着打印出来 for(int i=p_num-1;i>=0;i–) cout<<points[i].x<<" "<<points[i].y<<endl; } //广度优先搜索 void BFS(int init_id) { POS p,next_p; p.val=init_id; p.step=0; visited[p.val]=1; pre[p.val]=-1;//没有前一个状态 queue<POS> Q_P; Q_P.push(p); while(!Q_P.empty()) { p=Q_P.front(); Q_P.pop(); if(p.val==ALL_1) { print_result(p,init_id); return; } for(int i=0;i<4;i++) { int curr_xor=XOR[i];//i不同时，翻转异或的值也不同 for(int j=0;j<4;j++) { next_p.val=p.val; next_p.val^=0xf<<(4*(3-i));//横向翻转 next_p.val^=curr_xor<<(3-j);//纵向翻转 if(visited[next_p.val]==0) { visited[next_p.val]=1; next_p.step=p.step+1; pre[next_p.val]=p.val;//记录前一个状态值 trace[next_p.val].x=i+1;//注意输出的坐标是从1开始到4 trace[next_p.val].y=j+1;//所以这里加1 Q_P.push(next_p); } } } } } int main() { //freopen("input.txt","r",stdin); char c; int id=0; for(int i=0;i<4;i++) { for(int j=0;j<4;j++) { cin>>c; id<<=1;//id=id<<1; if(c==’-‘)//-:1;+:0 id+=1; } } BFS(id); return 0; } [/cpp] 这个版本的代码如果以C++提交，则TLE，如果用G++提交则AC，用时625MS，内存1788K，不知道是什么原因。]]>
Here “b” denotes pieces lying their black side up and “w” denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
Input
The input consists of 4 lines with 4 characters “w” or “b” each that denote game field position.
Output
Write to the output file a single integer number – the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it’s impossible to achieve the goal, then write the word “Impossible” (without quotes).
Sample Input
bwwb
bbwb
bwwb
bwww
Sample Output
4
Source
Northeastern Europe 2000
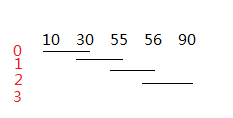左边的红色数字表示不同方案标号，这个标号也正好是该方案中数组a中的第一个插空位置的下标。很容易得到总的方案数有n-m+1个，所以我们只需将i从0到n-m+1循环枚举每一种方案，求最长的连续提交天数。
对于某一种方案，如上所述，其插空的开始下标正好为i，因为要插m个空，所以结束下标为m+i-1。那么这两者之间总的连续提交天数怎么算呢？比如上图中的方案2，如果把第55和56天填上，那么实际的连续提交天数应该是从31~89.也就是要从i-1对应的那天的后一天（31）算起，到m+i-1-1对应的那天的前一天（89）结束，总共就是89-31+1，也就是a[m+i-1+1]-a[i-1]-1；如果遇到最后一个空，因为m+i-1+1可能超过数组a的范围，所以我们添加一个a[n]=101，俗称哨兵；如果i==0的话，没有i-1，所以分开讨论。
最终的代码如下：
[cpp]
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int t;
cin>>t;
int n,m;
while(t–)
{
cin>>n>>m;
vector<int> a(n+1);
for(int i=0;i<n;i++)
cin>>a[i];
a[n]=101;//哨兵
if(m>=n)
cout<<100<<endl;
else
{
int max_days=0;//最长连续提交天数
int case_num=n-m+1;//总的枚举情况数
for(int i=0;i<case_num;i++)
{
int last_index=m+i-1;//该方案下最后一个下标
if(i==0)
{
if(a[last_index+1]-1>max_days)
max_days=a[last_index+1]-1;
}
else
{
if(a[last_index+1]-a[i-1]-1>max_days)
max_days=a[last_index+1]-a[i-1]-1;
}
}
cout<<max_days<<endl;
}
}
return 0;
}
[/cpp]
本代码提交AC，用时0MS，内存0MB。
]]>