LeetCode Range Sum Query – Mutable Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive. The update(i, val) function modifies nums by updating the element at index i to val. Example:
Given nums = [1, 3, 5] sumRange(0, 2) -> 9 update(1, 2) sumRange(0, 2) -> 8Note:
- The array is only modifiable by the update function.
- You may assume the number of calls to update and sumRange function is distributed evenly.
给定一个一维数组，要求实现范围求和，即求[i,j]之间的元素的和。sumRange(i,j)求i~j的元素和，update(i,val)更新下标为i的元素值为val。 第一敏感使用线段树，很久之前在hihoCoder上遇到过。 建树的方法是类似于树的后序遍历，即左右根。不断把[start,end]二分，构建左右子树，然后构建当前节点，当前节点的sum等于左右子树的sum的和。在递归的时候，递归到start==end时，说明只有一个元素了，此时sum就等于该元素。 查询的方法和建树方法类似，判断区间[i,j]和区间[start,end]的关系，假设start和end的中点是mid，如果j<=mid，递归在左子树查询；如果i>mid，递归在右子树查询；否则在[i,mid]和[mid+1,j]查询然后求和。 更新的方法和查询的方法类似，也是不断判断i和mid的关系，在左子树或者右子树递归更新，当找到该叶子节点时，更新它的sum，返回父节点也更新sum等于新的左右子树的sum的和。 完整代码如下： [cpp] class NumArray { private: struct Node { int start, end, sum; Node *left, *right; Node(int s, int e) :start(s), end(e), sum(0), left(NULL), right(NULL) {}; }; Node *root; Node* constructTree(vector<int> &nums, int start, int end) { Node* node = new Node(start, end); if (start == end) { node->sum = nums[start]; return node; } int mid = start + (end – start) / 2; node->left = constructTree(nums, start, mid); node->right = constructTree(nums, mid + 1, end); node->sum = node->left->sum + node->right->sum; return node; } int sumRange(int i, int j, Node *root) { if (root == NULL)return 0; if (i == root->start&&j == root->end)return root->sum; int mid = root->start + (root->end – root->start) / 2; if (j <= mid)return sumRange(i, j, root->left); else if (i > mid)return sumRange(i, j, root->right); else return sumRange(i, mid, root->left) + sumRange(mid + 1, j, root->right); } void update(int i, int val, Node *root) { if (root->start == root->end && root->start == i) { root->sum = val; return; } int mid = root->start + (root->end – root->start) / 2; if (i <= mid)update(i, val, root->left); else update(i, val, root->right); root->sum = root->left->sum + root->right->sum; } public: NumArray(vector<int> nums) { root = NULL; if (!nums.empty())root = constructTree(nums, 0, nums.size() – 1); } void update(int i, int val) { if (root == NULL)return; update(i, val, root); } int sumRange(int i, int j) { if (root == NULL)return 0; return sumRange(i, j, root); } }; [/cpp] 本代码提交AC，用时172MS。]]>
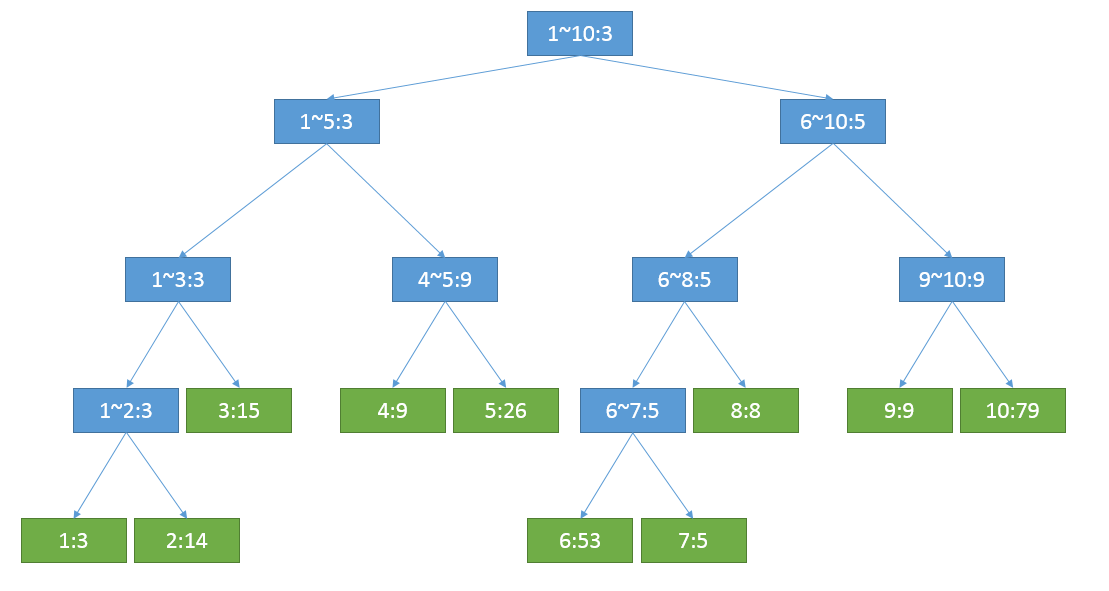上图是线段树的一个例子，每个节点保存了区间范围以及该区间的最小值。总的区间大小是[1,10]，仔细看看这个区间树的节点个数只有19个；另外再画一个[1,6]区间上的区间树，节点个数只有11个。可以不加证明的得出一个n的区间长度的线段树的节点个数为2*n-1，这远远小于n*n，所以我们只需要O(n)的空间来存储，而不是O(n^2)。
反观之前
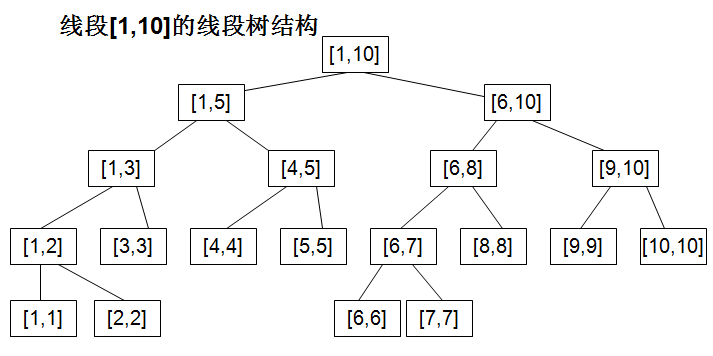从图中可以看到构造线段树的过程就是一个二分的过程，不断将区间分成两半，直到只有一个元素。图中的线段树每一个节点是一个区间[l,r]，本题我稍微改造了一下，改成了数组int seg_tree[left][length]，比如seg_tree[i][j]表示从下标i开始，长度为j的这样一个区间上的最小值，这样就可以利用线段树来解决RMQ问题了。比如改造后的线段树就成了下面的样子：
因为树形这种特殊的结构，我们可以用一个DFS来对树实现二分构造，当DFS到某个节点长度为1时，其最小值就是w[i]本身，在回溯到父节点时，父节那个区间的最小值又是所有子节点最小值中的最小值。因为树的总节点数大约为2*n，所以复杂度O(n)。
当需要查询区间[l,r]的最小值时，只需对数组seg_tree二分搜索。具体来说，假设我们搜索到了节点[s_l,s_len]，如果r<(s_l+s_len/2)，说明区间[l,r]全在[s_l,s_len]的左边，我们递归在[s_l,s_len/2]区间找；如果l>=(s_l+s_len/2)，说明区间[l,r]全在[s_l,s_len]的右边，我们递归在[s_l+s_len/2,s_len-s_len/2]区间找；如果以上两者都不是，说明[l,r]跨界了，而且中点下标一定是s_l+s_len/2，所以我们分别在二两半区间找，然后求这两者的最小值。复杂度O(lgn)。
当需要更新某个下标为pos的值为value时，也是DFS查找线段树，直到找到叶子seg_tree[pos][1]，更新它的值，以及所有我们在查找过程经过的父节点的值。复杂度O(lgn)。
所以线段是的性质使得无论是构造、查询、更新操作，复杂度都只要O(lgn)，这就是题目中所说的把总的复杂度平均分配到不同操作：平衡乃和谐之理。
完整代码如下：
[cpp]
#include<iostream>
using namespace std;
const int MAX_N=1e4+2;
int w[MAX_N];//每个商品重量
int n,m;
int seg_tree[MAX_N][MAX_N];//seg_tree[i][j]：起点为i，长度为j的区间的最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
//深度优先遍历以构造线段树
void dfs(int left,int length)
{
if(length==1)
{
seg_tree[left][1]=w[left];
return;
}
dfs(left,length/2);
dfs(left+length/2,length-length/2);
seg_tree[left][length]=get_min(seg_tree[left][length/2],seg_tree[left+length/2][length-length/2]);//取最小值
}
//在区间[s_left,s_len]搜索区间[left,length]的最小值
int search_min(int s_left,int s_len,int left,int length)
{
if((s_left==left)&&(s_len==length))
return seg_tree[s_left][s_len];
if((left+length-1)<(s_left+s_len/2))//全在左半部分
{
return search_min(s_left,s_len/2,left,length);
}
else if(left>=(s_left+s_len/2))//全在右半部分
{
return search_min(s_left+s_len/2,s_len-s_len/2,left,length);
}
else//左右分开搜索
{
int left_len=s_left+s_len/2-left;
int right_len=length-left_len;
int min_left=search_min(s_left,s_len/2,left,left_len);
int min_right=search_min(s_left+s_len/2,s_len-s_len/2,s_left+s_len/2,right_len);
return get_min(min_left,min_right);
}
}
//从区间[s_left,s_len]开始更新下标pos的值为value
void update(int s_left,int s_len,int pos,int value)
{
if((s_left==pos)&&(s_len==1))
{
seg_tree[s_left][1]=value;
return ;
}
int mid=s_left+s_len/2;
if(pos<mid)
update(s_left,s_len/2,pos,value);
else
update(mid,s_len-s_len/2,pos,value);
seg_tree[s_left][s_len]=get_min(seg_tree[s_left][s_len/2],seg_tree[mid][s_len-s_len/2]);//更新父节点
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
for(int i=1;i<=n;i++)
cin>>w[i];
dfs(1,n);
cin>>m;
int p,l,r;
for(int i=0;i<m;i++)
{
cin>>p>>l>>r;
if(p==0)//查询
{
cout<<search_min(1,n,l,r-l+1)<<endl;
}
else//修改
{
update(1,n,l,r);
}
}
return 0;
}
[/cpp]
本代码提交AC，用时151MS，内存42MB。
]]>