POJ 1125-Stockbroker Grapevine Stockbroker Grapevine Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 27559 Accepted: 15273 Description Stockbrokers are known to overreact to rumours. You have been contracted to develop a method of spreading disinformation amongst the stockbrokers to give your employer the tactical edge in the stock market. For maximum effect, you have to spread the rumours in the fastest possible way. Unfortunately for you, stockbrokers only trust information coming from their “Trusted sources” This means you have to take into account the structure of their contacts when starting a rumour. It takes a certain amount of time for a specific stockbroker to pass the rumour on to each of his colleagues. Your task will be to write a program that tells you which stockbroker to choose as your starting point for the rumour, as well as the time it will take for the rumour to spread throughout the stockbroker community. This duration is measured as the time needed for the last person to receive the information. Input Your program will input data for different sets of stockbrokers. Each set starts with a line with the number of stockbrokers. Following this is a line for each stockbroker which contains the number of people who they have contact with, who these people are, and the time taken for them to pass the message to each person. The format of each stockbroker line is as follows: The line starts with the number of contacts (n), followed by n pairs of integers, one pair for each contact. Each pair lists first a number referring to the contact (e.g. a ‘1’ means person number one in the set), followed by the time in minutes taken to pass a message to that person. There are no special punctuation symbols or spacing rules. Each person is numbered 1 through to the number of stockbrokers. The time taken to pass the message on will be between 1 and 10 minutes (inclusive), and the number of contacts will range between 0 and one less than the number of stockbrokers. The number of stockbrokers will range from 1 to 100. The input is terminated by a set of stockbrokers containing 0 (zero) people. Output For each set of data, your program must output a single line containing the person who results in the fastest message transmission, and how long before the last person will receive any given message after you give it to this person, measured in integer minutes. It is possible that your program will receive a network of connections that excludes some persons, i.e. some people may be unreachable. If your program detects such a broken network, simply output the message “disjoint”. Note that the time taken to pass the message from person A to person B is not necessarily the same as the time taken to pass it from B to A, if such transmission is possible at all. Sample Input 3 2 2 4 3 5 2 1 2 3 6 2 1 2 2 2 5 3 4 4 2 8 5 3 1 5 8 4 1 6 4 10 2 7 5 2 2 2 5 1 5 Sample Output 3 2 3 10 Source Southern African 2001
首先读懂题意。Stockbroker想要给每一个人传播谣言，问从哪一个人开始传播，可以使谣言传播得最快，并求最快的传播时间是多少。转换成数据结构的语言就是：给你一张图，问从哪一点到其他所有点的最短距离中的最长者最短。表述起来有点绕，下面用图示来说明。
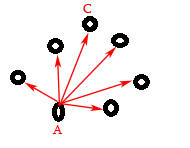
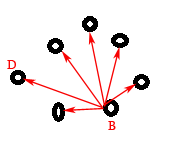假设分别从A点和B点开始的单源最短距离如上两张图所示，那么Stockbroker从A点开始传播谣言总共需要多长时间呢？因为传播是可以同时进行的，所以传播结束时间就是A点到其他点中的最长距离，也就是上图中的AC。同理，如果从B点开始，则|BD|是传播时间。
综上所述，本题的求解过程可以归纳为以下几步：
1. 测试图中的每一个点$$i$$，求从该点出发，到其他所有点的单源最短距离集合$$S_i$$
2. 求出该单源最短距离$$S_i$$内部的最大值$$M_i$$
3. 对于图中的所有点，求其$$M_i$$
4. 最后求所有$$M_i$$中的最小值$$MIN$$，即为最终结果
所以根据上面的步骤，我们可以用n次Dijkstra算法求每个点的单源最短距离内部的最大值$$M_i$$，然后求$$MIN$$。其实也可以不用这么麻烦，因为我们还有另外一个更简单的算法Floyd算法。使用Floyd算法求得所有点对的最短距离，自然就知道某个点的单源最短距离了。
在写代码的时候还有一些小问题需要注意，对于数据输入，请仔细多读几遍Input说明，如果还是有困难，请看这里，题目还要求如果是非连通图，输出disjoint，那么怎么来判断是否是非连通图呢？我使用的方法是：