LeetCode Optimal Division Given a list of positive integers, the adjacent integers will perform the float division. For example, [2,3,4] -> 2 / 3 / 4. However, you can add any number of parenthesis at any position to change the priority of operations. You should find out how to add parenthesis to get the maximum result, and return the corresponding expression in string format. Your expression should NOT contain redundant parenthesis. Example:
Input: [1000,100,10,2] Output: "1000/(100/10/2)" Explanation: 1000/(100/10/2) = 1000/((100/10)/2) = 200 However, the bold parenthesis in "1000/((100/10)/2)" are redundant, since they don't influence the operation priority. So you should return "1000/(100/10/2)". Other cases: 1000/(100/10)/2 = 50 1000/(100/(10/2)) = 50 1000/100/10/2 = 0.5 1000/100/(10/2) = 2Note:
- The length of the input array is [1, 10].
- Elements in the given array will be in range [2, 1000].
- There is only one optimal division for each test case.
给定一个正整数数组,数据范围是[2,1000],初始每个数依次除以后一个数,现在要给数组加上括号,使得整个数组相除的结果最大。 首先来个暴力方法,对区间[start, end],枚举每一个分割位置i,也就是[start, i]算除法,[i+1, end]也算除法,然后把前者的结果除以后者。结果的最大值为前者的最大值除以后者的最小值,结果的最小值为前者的最小值除以后者的最大值。一直递归下去,最后就能得到整个区间[0,n-1]的最大值了。 代码如下: [cpp] struct T { double lfMax, lfMin; string strMax, strMin; }; class Solution { private: T optimal(vector<int>& nums, int start, int end){ T t; if(start == end){ t.lfMax = t.lfMin = nums[start]; t.strMax = t.strMin = to_string(nums[start]); return t; } t.lfMax = std::numeric_limits<double>::min(); t.lfMin = std::numeric_limits<double>::max(); for(int i = start; i < end; ++i){ T tl = optimal(nums, start, i); T tr = optimal(nums, i + 1, end); if(tl.lfMax / tr.lfMin > t.lfMax){ t.lfMax = tl.lfMax / tr.lfMin; t.strMax = tl.strMax + "/" + (i + 1 != end ? "(" : "") + tr.strMin + (i + 1 != end ? ")" : ""); } if(tl.lfMin / tr.lfMax < t.lfMin){ t.lfMin = tl.lfMin / tr.lfMax; t.strMin = tl.strMin + "/" + (i + 1 != end ? "(" : "") + tr.strMax + (i + 1 != end ? ")" : ""); } } return t; } public: string optimalDivision(vector<int>& nums) { T t = optimal(nums, 0, nums.size() – 1); return t.strMax; } }; [/cpp] 本代码提交AC,用时86MS。暴力方法相当于枚举数组的所有排列情况,时间复杂度为O(n!)。 上述方法对某一小段区间会有很多重复计算,我们可以用数组把结果存起来达到加速的目的。使用数组memo[i][j]存储[i,j]的最大值最小值结果,递归的时候如果发现memo[start][end]已经有结果了,则直接返回。代码如下: [cpp] struct T { double lfMax, lfMin; string strMax, strMin; }; class Solution { private: T optimal(vector<int>& nums, int start, int end, vector<vector<T>>& memo){ if(memo[start][end].strMax != "" || memo[start][end].strMin != "") return memo[start][end]; T t; if(start == end){ t.lfMax = t.lfMin = nums[start]; t.strMax = t.strMin = to_string(nums[start]); memo[start][end] = t; return t; } t.lfMax = std::numeric_limits<double>::min(); t.lfMin = std::numeric_limits<double>::max(); for(int i = start; i < end; ++i){ T tl = optimal(nums, start, i, memo); T tr = optimal(nums, i + 1, end, memo); if(tl.lfMax / tr.lfMin > t.lfMax){ t.lfMax = tl.lfMax / tr.lfMin; t.strMax = tl.strMax + "/" + (i + 1 != end ? "(" : "") + tr.strMin + (i + 1 != end ? ")" : ""); } if(tl.lfMin / tr.lfMax < t.lfMin){ t.lfMin = tl.lfMin / tr.lfMax; t.strMin = tl.strMin + "/" + (i + 1 != end ? "(" : "") + tr.strMax + (i + 1 != end ? ")" : ""); } } memo[start][end] = t; return t; } public: string optimalDivision(vector<int>& nums) { vector<vector<T>> memo(nums.size(), vector<T>(nums.size())); T t = optimal(nums, 0, nums.size() – 1, memo); return t.strMax; } }; [/cpp] 本代码提交AC,用时6MS。一下快了不少。 还有一种纯数学的方法。假设我们要对a/b/c/d加括号使得结果最大,则a肯定是分子不能动了,那么就相当于最小化b/c/d。b/c/d有两种加括号的方案:b/(c/d)和(b/c)/d。如果令b/(c/d)>b/c/d,因为b,c,d都是正数,推出d>1。又题目中的数据范围是[2,1000],所以b/(c/d)>b/c/d显然成立。也就是b/c/d这种方案是最小的,使得a/(b/c/d)结果最大。所以只需要把a后面的数加一个括号整体括起来就好了。 代码如下: [cpp] class Solution { public: string optimalDivision(vector<int>& nums) { int n = nums.size(); if(n == 1) return to_string(nums[0]); else if(n == 2) return to_string(nums[0]) + "/" + to_string(nums[1]); string ans = to_string(nums[0]) + "/("; for(int i = 1; i < n – 1; ++i){ ans += to_string(nums[i]) + "/"; } return ans + to_string(nums[n-1]) + ")"; } }; [/cpp] 本代码提交AC,用时3MS。 参考:https://leetcode.com/articles/optimal-division/]]>
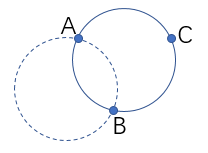 已知两点求圆心的方法请看
已知两点求圆心的方法请看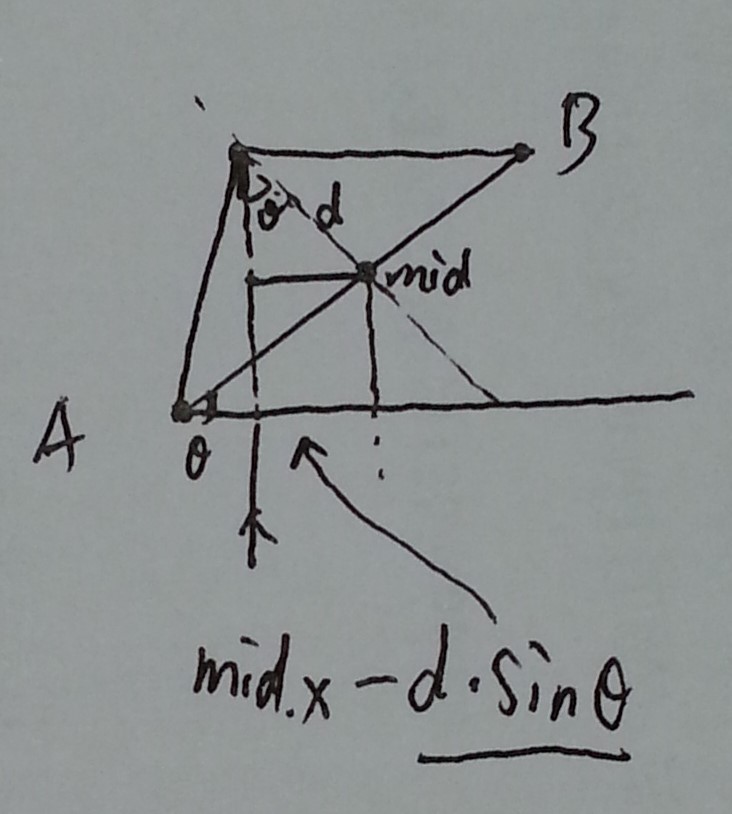 暴力方法在hiho上TLE,需要寻求更高效的算法。
假设以两个点i,j为圆心画半径为R的圆,如果两个圆相交,则在相交的弧上任意一点画圆,都能覆盖原来的i,j两点。基于这个思想,假设现在固定点i为圆心,R为半径画圆,求出所有以其他点为圆心画的圆和圆i相交的弧,则在相交重叠次数最多的那段弧上的点为圆心画的圆肯定能覆盖最多的点,覆盖的点数就是这段弧被重叠的次数。每个点i都能求出这样一个最大值,则所有点的这个最大值的最大值就是全局能覆盖的最多点。
怎样表示两个圆相交的那段弧呢,使用极坐标,因为弧是由两条半径张成的,所以可以表示成两条半径的极坐标夹角,并且标明夹角的开始(is=1)和结束(is=-1)。求重叠次数最多的弧的方法是,把所有重叠弧的起止半径的极坐标夹角排个序,然后遍历一下,当夹角开始(is=1)次数最多且结束(is=-1)次数最少时,说明重叠次数最多,所以就是is的累加和的最大值。
完整代码借鉴
暴力方法在hiho上TLE,需要寻求更高效的算法。
假设以两个点i,j为圆心画半径为R的圆,如果两个圆相交,则在相交的弧上任意一点画圆,都能覆盖原来的i,j两点。基于这个思想,假设现在固定点i为圆心,R为半径画圆,求出所有以其他点为圆心画的圆和圆i相交的弧,则在相交重叠次数最多的那段弧上的点为圆心画的圆肯定能覆盖最多的点,覆盖的点数就是这段弧被重叠的次数。每个点i都能求出这样一个最大值,则所有点的这个最大值的最大值就是全局能覆盖的最多点。
怎样表示两个圆相交的那段弧呢,使用极坐标,因为弧是由两条半径张成的,所以可以表示成两条半径的极坐标夹角,并且标明夹角的开始(is=1)和结束(is=-1)。求重叠次数最多的弧的方法是,把所有重叠弧的起止半径的极坐标夹角排个序,然后遍历一下,当夹角开始(is=1)次数最多且结束(is=-1)次数最少时,说明重叠次数最多,所以就是is的累加和的最大值。
完整代码借鉴