Sort a linked list using insertion sort.

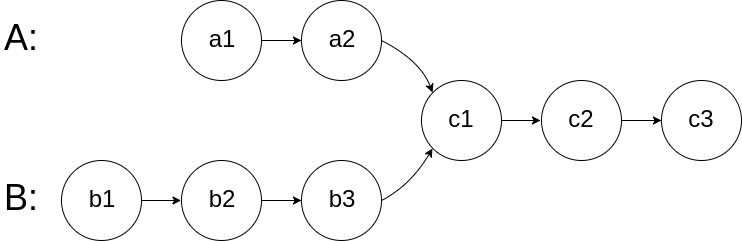
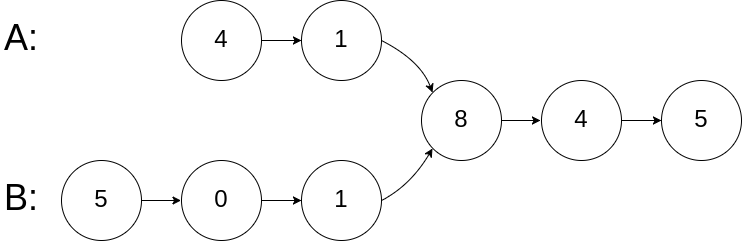
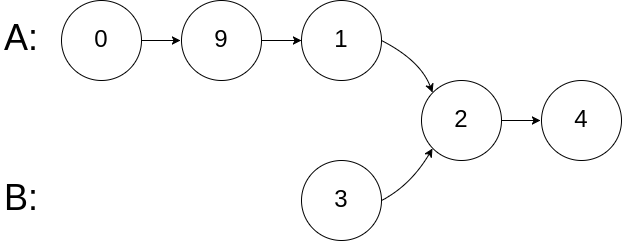
A graphical example of insertion sort. The partial sorted list (black) initially contains only the first element in the list.
With each iteration one element (red) is removed from the input data and inserted in-place into the sorted list
Algorithm of Insertion Sort:
- Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list.
- At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there.
- It repeats until no input elements remain.
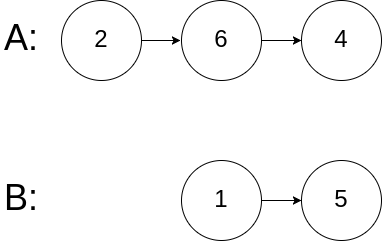
Example 1:
Input: 4->2->1->3 Output: 1->2->3->4
Example 2:
Input: -1->5->3->4->0 Output: -1->0->3->4->5
对一个链表进行插入排序。 简单题,每次从原链表中断一个节点下来,然后在新的有序链表中线性查找插入的位置。这里有个技巧,有可能链表的第一个节点很大,后续节点需要插入表头;也可能后续节点很大,需要插入表尾;还可能是不大不小,插入中间。情况比较多,为了方便统一代码形式,可以在新的有序链表的表头插入一个INT_MIN的最小节点,这样所有代码都统一了,也不容易出错。 完整代码如下:
class Solution {
public:
ListNode* insertionSortList(ListNode* head)
{
if (head == NULL || head->next == NULL)
return head;
ListNode* newHead = new ListNode(INT_MIN);
newHead->next = head;
head = head->next;
newHead->next->next = NULL;
while (head) {
ListNode *insertPos = newHead->next, *pre = newHead;
while (insertPos && insertPos->val < head->val) {
insertPos = insertPos->next;
pre = pre->next;
}
ListNode* tmp = head;
head = head->next;
tmp->next = insertPos;
pre->next = tmp;
}
return newHead->next;
}
};本代码提交AC,用时59MS。
二刷。需要注意如果测试数据中含有INT_MIN的情况:
class Solution {
public:
ListNode* insertionSortList(ListNode* head) {
if (head == NULL || head->next == NULL)return head;
ListNode *dummy = new ListNode(INT_MIN);
ListNode *l1 = head, *l2 = head;
while (l1 != NULL) {
l2 = l1->next;
ListNode *l3 = dummy, *l3_pre = dummy;
while (l3 != NULL && l1->val > l3->val) {
l3_pre = l3;
l3 = l3->next;
}
if (l1->val == INT_MIN) {
l1->next = dummy->next;
dummy->next = l1;
}
else {
l1->next = l3;
l3_pre->next = l1;
}
l1 = l2;
}
return dummy->next;
}
};本代码提交AC,用时48MS。