POJ 1258-Agri-Net Agri-Net Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 40975 Accepted: 16713 Description Farmer John has been elected mayor of his town! One of his campaign promises was to bring internet connectivity to all farms in the area. He needs your help, of course. Farmer John ordered a high speed connection for his farm and is going to share his connectivity with the other farmers. To minimize cost, he wants to lay the minimum amount of optical fiber to connect his farm to all the other farms. Given a list of how much fiber it takes to connect each pair of farms, you must find the minimum amount of fiber needed to connect them all together. Each farm must connect to some other farm such that a packet can flow from any one farm to any other farm. The distance between any two farms will not exceed 100,000. Input The input includes several cases. For each case, the first line contains the number of farms, N (3 <= N <= 100). The following lines contain the N x N conectivity matrix, where each element shows the distance from on farm to another. Logically, they are N lines of N space-separated integers. Physically, they are limited in length to 80 characters, so some lines continue onto others. Of course, the diagonal will be 0, since the distance from farm i to itself is not interesting for this problem. Output For each case, output a single integer length that is the sum of the minimum length of fiber required to connect the entire set of farms. Sample Input 4 0 4 9 21 4 0 8 17 9 8 0 16 21 17 16 0 Sample Output 28 Source USACO 102
这一题相对第2485来说就更是彻头彻尾的最小生成树了。它要求的是最小生成树的总长度，所以对2485稍微修改即可。需要注意的是题目中有这么一句话：
The input includes several cases.也就是说有多个测试用例，而不是直接告诉你有几个用例或者结束标志是0 0 0之类的，我一开始写成了 [cpp] while(1) { scanf("%d",&n); … } [/cpp] 这样就变成了有无穷个测试用例了，根本停不下来，所以Time Limit Exceeded好几次，后来改成这样就好了： [cpp] while(scanf("%d",&n)!=EOF) { … } [/cpp] 完整的代码如下： [cpp] #include<stdio.h> int a[101][101]; int lowcost[101]; //int closet[101]; const static int MAX_DIS=100001; //最长距离 //prim算法求最小生成树 int prim(int n) { for(int i=0;i<n;i++) { lowcost[i]=a[0][i]; //closet[i]=0;//这个数组可以不要 } int total_min_len=0; int k,curr_min_len; for(int t=0;t<n-1;t++) { k=0; curr_min_len=MAX_DIS; for(int i=0;i<n;i++) { if(lowcost[i]!=0&&lowcost[i]<curr_min_len) { curr_min_len=lowcost[i]; k=i; } } total_min_len+=curr_min_len;//这题才是求和 //if(curr_min_len>total_min_len)//注意看题，求最小生成树中的最长路径 // total_min_len=curr_min_len; lowcost[k]=0; for(int i=0;i<n;i++) { if(a[i][k]!=0&&a[i][k]<lowcost[i]) { lowcost[i]=a[i][k]; //closet[i]=k; } } } return total_min_len; } int main() { int n; //while(1)//The input includes several cases.并不代表case无穷 while(scanf("%d",&n)!=EOF) { //scanf("%d",&n); for(int i=0;i<n;i++) for(int j=0;j<n;j++) scanf("%d",&a[i][j]); printf("%d\n",prim(n)); } return 0; } [/cpp] 本代码提交AC，用时16MS，内存172K。可以看到内存明显比2485题少了，那是因为我把closet数组删了，因为常规的最小生成树不需要这个变量。]]>
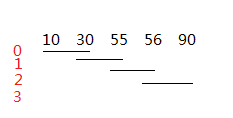左边的红色数字表示不同方案标号，这个标号也正好是该方案中数组a中的第一个插空位置的下标。很容易得到总的方案数有n-m+1个，所以我们只需将i从0到n-m+1循环枚举每一种方案，求最长的连续提交天数。
对于某一种方案，如上所述，其插空的开始下标正好为i，因为要插m个空，所以结束下标为m+i-1。那么这两者之间总的连续提交天数怎么算呢？比如上图中的方案2，如果把第55和56天填上，那么实际的连续提交天数应该是从31~89.也就是要从i-1对应的那天的后一天（31）算起，到m+i-1-1对应的那天的前一天（89）结束，总共就是89-31+1，也就是a[m+i-1+1]-a[i-1]-1；如果遇到最后一个空，因为m+i-1+1可能超过数组a的范围，所以我们添加一个a[n]=101，俗称哨兵；如果i==0的话，没有i-1，所以分开讨论。
最终的代码如下：
[cpp]
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int t;
cin>>t;
int n,m;
while(t–)
{
cin>>n>>m;
vector<int> a(n+1);
for(int i=0;i<n;i++)
cin>>a[i];
a[n]=101;//哨兵
if(m>=n)
cout<<100<<endl;
else
{
int max_days=0;//最长连续提交天数
int case_num=n-m+1;//总的枚举情况数
for(int i=0;i<case_num;i++)
{
int last_index=m+i-1;//该方案下最后一个下标
if(i==0)
{
if(a[last_index+1]-1>max_days)
max_days=a[last_index+1]-1;
}
else
{
if(a[last_index+1]-a[i-1]-1>max_days)
max_days=a[last_index+1]-a[i-1]-1;
}
}
cout<<max_days<<endl;
}
}
return 0;
}
[/cpp]
本代码提交AC，用时0MS，内存0MB。
]]>
要判断给出的点是否只有4个点，第一反应是用set集合，只要把题目给出的8个点都加入到set中，判断集合大小是否是4就可以了。
首先给出点的定义：
[cpp]
//点结构体
typedef struct P
{
int x,y;//两点坐标
bool operator<(const P& p)const//如果要加入到set中，需要重载<
{
//return this->x<p.x&&this->y<p.y;//注意这样会导致(0,0)<(0,1)且(0,1)<(0,0)的情况
return (this->x<p.x)||((this->x==p.x)&&(this->y<p.y));
}
bool operator==(const P&p)const//重载等于比较
{
return (this->x==p.x)&&(this->y==p.y);
}
};
[/cpp]
需要注意一点，因为需要把P加入到set中，而set是通过红黑树来排序的，所以需要重载小于<操作符。我最开始重载函数是这样写的
[cpp]
return this->x<p.x&&this->y<p.y;
[/cpp]
但是这样会有问题，如果给出两个点(0,0)和(0,1)，会得出(0,0)<(0,1)和(0,1)<(0,0)都不成立的结论，也就是说无法给(0,0)和(0,1)排序，也就无法插入到set中，所以需要修改成
[cpp]
return (this->x<p.x)||((this->x==p.x)&&(this->y<p.y));
[/cpp]
这样就能判断(0,0)<(0,1)成立了。有关这个问题可以参考