HDOJ 5424-Rikka with Graph II Rikka with Graph II Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 379 Accepted Submission(s): 94 Problem Description As we know, Rikka is poor at math. Yuta is worrying about this situation, so he gives Rikka some math tasks to practice. There is one of them: Yuta has a non-direct graph with n vertices and n edges. Now he wants you to tell him if there exist a Hamiltonian path. It is too difficult for Rikka. Can you help her? Input There are no more than 100 testcases. For each testcase, the first line contains a number n(1≤n≤1000). Then n lines follow. Each line contains two numbers u,v(1≤u,v≤n) , which means there is an edge between u and v. Output For each testcase, if there exist a Hamiltonian path print “YES” , otherwise print “NO”. Sample Input 4 1 1 1 2 2 3 2 4 3 1 2 2 3 3 1 Sample Output NO YES Hint For the second testcase, One of the path is 1->2->3 If you doesn’t know what is Hamiltonian path, click here (https://en.wikipedia.org/wiki/Hamiltonian_path). Source BestCoder Round #53 (div.2) Recommend hujie | We have carefully selected several similar problems for you: 5426 5425 5424 5423 5422
这题题意很明确,判断一个无向图中是否存在哈密顿路径,注意不是哈密顿回路。
由指定的起点前往指定的终点,途中经过所有其他节点且只经过一次,形成的路径称为哈密顿路径,闭合的哈密顿路径称作哈密顿回路,含有哈密顿回路的图称为哈密顿图。本来判断一个常规图中是否存在哈密顿路径是NP完全问题,不可能有多项式解,所以如果依次对每个点DFS,肯定超时。 但是这题很特殊,图中只有n个点,n条边!如果存在哈密顿路径L,则路径长度为n-1条边,设L两个端点为A,B,此时还剩下一条边a,这条边有三种情况: 1)a在L的内部连接,这时A,B的度数都为1,其他点的度数为2或3; 2)a一端在A(或B),另一端在L的内部,这时L的另一个端点B(或A)的度数为1,其他点的度数为2或3; 3)a连接了A,B,此时所有点的度数都为2。 如果存在哈密顿路径,这三种情况下,L的某个端点的度数都是最少的。所以可以先找到度数最小的点,再从这个点开始DFS,这样只需要一次DFS就可以判断是否存在哈密顿路径。 当然要先判断这个图是否连通,我起初使用了并查集,但是超时,郁闷。后来发现,如果哈密顿路径存在,则肯定连通,且此时读数为1点不超过2个,所以可以用这个条件判断是否连通。 完整代码如下: [cpp] #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cstdlib> #include<vector> using namespace std; const int kMaxN = 1005; int degree[kMaxN]; vector<vector<int>> path; int visit[kMaxN]; int n, done; bool DFS(int s) { done++; visit[s] = 1; if (done == n) return true; int v; for (int i = 0; i < path[s].size(); i++) { v = path[s][i]; if (!visit[v]) { if (DFS(v)) return true; } } done–; visit[s] = 0; return false; } bool CheckHamiltonian() { int min_degree = n + 1, bad_node_num = 0, id; for (int i = 1; i <= n; i++) { if (degree[i] && degree[i] < min_degree) { min_degree = degree[i]; id = i; } if (degree[i] <= 1) bad_node_num++; } if (bad_node_num > 2) return false; memset(visit, 0, sizeof(visit)); done = 0; return DFS(id); } int main() { //freopen("input.txt", "r", stdin); while (~scanf("%d", &n)) { memset(degree, 0, sizeof(degree)); path.clear(); path.resize(n + 1); int u, v; for (int i = 0; i < n; i++) { scanf("%d %d", &u, &v); if (u == v) continue; degree[u]++; degree[v]++; path[u].push_back(v); path[v].push_back(u); } if (CheckHamiltonian()) printf("YES\n"); else printf("NO\n"); } return 0; } [/cpp] 本代码提交AC,用时93MS,内存1800K。]]>
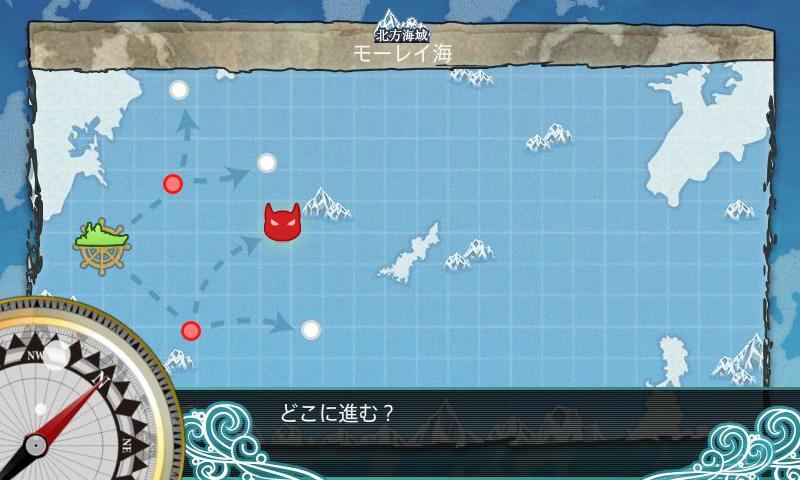 其中红色的点表示有敌人驻扎,猫头像的的点表示该地图敌军主力舰队(boss)的驻扎点,虚线表示各个战略点之间的航线(无向边)。
在游戏中要从一个战略点到相邻战略点需要满足一定的条件,即需要舰队的索敌值大于等于这两点之间航线的索敌值需求。
由于提高索敌值需要将攻击机、轰炸机换成侦察机,舰队索敌值越高,也就意味着舰队的战力越低。
另外在每一个战略点会发生一次战斗,需要消耗1/K的燃料和子弹。必须在燃料和子弹未用完的情况下进入boss点才能与boss进行战斗,所以舰队最多只能走过K条航路。
现在Nettle想要以最高的战力来进攻boss点,所以他希望能够找出一条从起始点(编号为1的点)到boss点的航路,使得舰队需要达到的索敌值最低,并且有剩余的燃料和子弹。
特别说明:两个战略点之间可能不止一条航线,两个相邻战略点之间可能不止一条航线。保证至少存在一条路径能在燃料子弹用完前到达boss点。
提示:你在找什么?
输入
第1行:4个整数N,M,K,T。N表示战略点数量,M表示航线数量,K表示最多能经过的航路,T表示boss点编号, 1≤N,K≤10,000, N≤M≤100,000
第2..M+1行:3个整数u,v,w,表示战略点u,v之间存在航路,w表示该航路需求的索敌值,1≤w≤1,000,000。
输出
第1行:一个整数,表示舰队需要的最小索敌值。
样例输入
5 6 2 5
1 2 3
1 3 2
1 4 4
2 5 2
3 5 5
4 5 3
样例输出
3
其中红色的点表示有敌人驻扎,猫头像的的点表示该地图敌军主力舰队(boss)的驻扎点,虚线表示各个战略点之间的航线(无向边)。
在游戏中要从一个战略点到相邻战略点需要满足一定的条件,即需要舰队的索敌值大于等于这两点之间航线的索敌值需求。
由于提高索敌值需要将攻击机、轰炸机换成侦察机,舰队索敌值越高,也就意味着舰队的战力越低。
另外在每一个战略点会发生一次战斗,需要消耗1/K的燃料和子弹。必须在燃料和子弹未用完的情况下进入boss点才能与boss进行战斗,所以舰队最多只能走过K条航路。
现在Nettle想要以最高的战力来进攻boss点,所以他希望能够找出一条从起始点(编号为1的点)到boss点的航路,使得舰队需要达到的索敌值最低,并且有剩余的燃料和子弹。
特别说明:两个战略点之间可能不止一条航线,两个相邻战略点之间可能不止一条航线。保证至少存在一条路径能在燃料子弹用完前到达boss点。
提示:你在找什么?
输入
第1行:4个整数N,M,K,T。N表示战略点数量,M表示航线数量,K表示最多能经过的航路,T表示boss点编号, 1≤N,K≤10,000, N≤M≤100,000
第2..M+1行:3个整数u,v,w,表示战略点u,v之间存在航路,w表示该航路需求的索敌值,1≤w≤1,000,000。
输出
第1行:一个整数,表示舰队需要的最小索敌值。
样例输入
5 6 2 5
1 2 3
1 3 2
1 4 4
2 5 2
3 5 5
4 5 3
样例输出
3
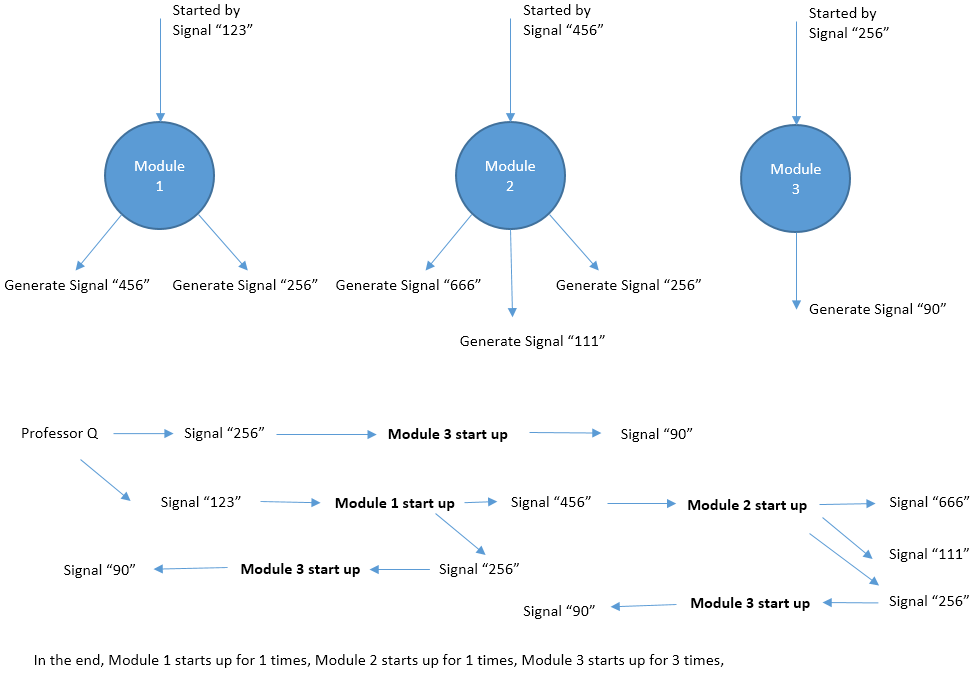 输入
The first line contains an integer T, the number of test cases. T test cases follows.
For each test case, the first line contains contains two numbers N and M, indicating the number of modules and number of signals that Professor Q generates initially.
The second line contains M integers, indicating the signals that Professor Q generates initially.
Line 3~N + 2, each line describes an module, following the format S, K, E1, E2, … , EK. S represents the signal that start up this module. K represents the total amount of signals that are generated during the lifecircle of this module. And E1 … EK are these signals.
For 20% data, all N, M <= 10
For 40% data, all N, M <= 103
For 100% data, all 1 <= T <= 5, N, M <= 105, 0 <= K <= 3, 0 <= S, E <= 105.
Hint: HUGE input in this problem. Fast IO such as scanf and BufferedReader are recommended.
输出
For each test case, output a line with N numbers Ans1, Ans2, … , AnsN. Ansi is the number of times that the i-th module is started. In case the answers may be too large, output the answers modulo 142857 (the remainder of division by 142857).
样例输入
3
3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90
3 1
100
100 2 200 200
200 1 300
200 0
5 1
1
1 2 2 3
2 2 3 4
3 2 4 5
4 2 5 6
5 2 6 7
样例输出
1 1 3
1 2 2
1 1 2 3 5
输入
The first line contains an integer T, the number of test cases. T test cases follows.
For each test case, the first line contains contains two numbers N and M, indicating the number of modules and number of signals that Professor Q generates initially.
The second line contains M integers, indicating the signals that Professor Q generates initially.
Line 3~N + 2, each line describes an module, following the format S, K, E1, E2, … , EK. S represents the signal that start up this module. K represents the total amount of signals that are generated during the lifecircle of this module. And E1 … EK are these signals.
For 20% data, all N, M <= 10
For 40% data, all N, M <= 103
For 100% data, all 1 <= T <= 5, N, M <= 105, 0 <= K <= 3, 0 <= S, E <= 105.
Hint: HUGE input in this problem. Fast IO such as scanf and BufferedReader are recommended.
输出
For each test case, output a line with N numbers Ans1, Ans2, … , AnsN. Ansi is the number of times that the i-th module is started. In case the answers may be too large, output the answers modulo 142857 (the remainder of division by 142857).
样例输入
3
3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90
3 1
100
100 2 200 200
200 1 300
200 0
5 1
1
1 2 2 3
2 2 3 4
3 2 4 5
4 2 5 6
5 2 6 7
样例输出
1 1 3
1 2 2
1 1 2 3 5