hihoCoder week 55-1-连通性·四
题目1 : 连通性·四
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi和小Ho从约翰家回到学校时,网络所的老师又找到了小Hi和小Ho。
老师告诉小Hi和小Ho:之前的分组出了点问题,当服务器(上次是连接)发生宕机的时候,在同一组的服务器有可能连接不上,所以他们希望重新进行一次分组。这一次老师希望对连接进行分组,并把一个组内的所有连接关联的服务器也视为这个组内的服务器(注意一个服务器可能属于多个组)。
这一次的条件是对于同一个组满足:当组内任意一个服务器宕机之后,不会影响组内其他服务器的连通性。在满足以上条件下,每个组内的边数量越多越好。
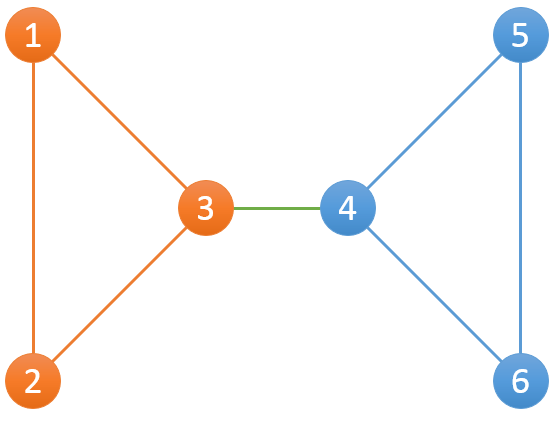
比如下面这个例子,一共有6个服务器和7条连接:
 其中包含3个组,分别为{(1,2),(2,3),(3,1)},{(4,5),(5,6),(4,6)},{(3,4)}。对{(1,2),(2,3),(3,1)}而言,和该组边相关联的有{1,2,3}三个服务器:当1宕机后,仍然有2-3可以连接2和3;当2宕机后,仍然有1-3可以连接1和3;当3宕机后,仍然有1-2可以连接1和2。
其中包含3个组,分别为{(1,2),(2,3),(3,1)},{(4,5),(5,6),(4,6)},{(3,4)}。对{(1,2),(2,3),(3,1)}而言,和该组边相关联的有{1,2,3}三个服务器:当1宕机后,仍然有2-3可以连接2和3;当2宕机后,仍然有1-3可以连接1和3;当3宕机后,仍然有1-2可以连接1和2。
 老师把整个网络的情况告诉了小Hi和小Ho,希望小Hi和小Ho统计一下一共有多少个分组。
提示:点的双连通分量
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。第i+1行表示存在一条边(u,v),编号为i,连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:1个整数,表示该网络的连接组数。
第2行:M个整数,第i个数表示第i条连接所属组内,编号最小的连接的编号。比如分为{(1,2)[1],(2,3)[3],(3,1)[2]},{(4,5)[5],(5,6)[7],(4,6)[6]},{(3,4)[4]},方括号内表示编号,则输出{1,1,1,4,5,5,5}。
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3
1 1 1 4 5 5 5
老师把整个网络的情况告诉了小Hi和小Ho,希望小Hi和小Ho统计一下一共有多少个分组。
提示:点的双连通分量
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。第i+1行表示存在一条边(u,v),编号为i,连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:1个整数,表示该网络的连接组数。
第2行:M个整数,第i个数表示第i条连接所属组内,编号最小的连接的编号。比如分为{(1,2)[1],(2,3)[3],(3,1)[2]},{(4,5)[5],(5,6)[7],(4,6)[6]},{(3,4)[4]},方括号内表示编号,则输出{1,1,1,4,5,5,5}。
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3
1 1 1 4 5 5 5
这一题求点的双连通分量,结果是边集;上一题求了边的双连通分量,结果是点集。 点的双连通分量是指子图中去掉一个点之后还连通,求解方法还是Tarjan,和之前的题目类似。需要注意的是,提示中的伪代码有错误,有好几个地方没有将边添加到堆栈中,正确的伪代码在这里。 本题要求输出连通分量中边的最小编号,所以输入的时候要记录边的编号,并且保证当弹出堆栈时,能快速知道这是哪一条边,简单的方法是将边(u,v)映射成一个整数x,因为u,v≤20,000,所以可以令hash=max(u,v)*100000+min(u,v)。 因为点的双连通分量数等于割点数量加1,如果DFS求到有2个割点,实际有3个连通分量,所以当DFS结束时,所有没有标记的边就是最后一个连通分量。 完整代码如下: [cpp] #include<iostream> #include<cstdio> #include<vector> #include<map> #include<stack> #include<algorithm> using namespace std; const int kMaxN = 20005; const int kMaxM = 100005; map<int, int> edge_code; map<int, int> ans; vector<vector<int> > graph; vector<int> edges; stack<int> stk; bool visit[kMaxN]; int low[kMaxN]; int dfn[kMaxN]; int parent[kMaxN]; int n, m; int points=0; int HashEdge(int x, int y) { if (x > y) return x * 100000 + y; else return y * 100000 + x; } void dfs(int u) { //记录dfs遍历次序 static int counter = 0; //记录节点u的子树数 int children = 0; visit[u] = true; //初始化dfn与low dfn[u] = low[u] = ++counter; for (int i = 0; i < graph[u].size(); i++) { int v = graph[u][i]; int e = HashEdge(u, v); if (ans.find(e)!=ans.end()) continue; //节点v未被访问,则(u,v)为树边 if (!visit[v]) { children++; parent[v] = u; stk.push(e); dfs(v); low[u] = min(low[u], low[v]); //case (1) if (parent[u] == 0 && children > 1) { points++; int tmp = -1, id = kMaxM; vector<int> tmp_edges; do{ tmp = stk.top(); stk.pop(); tmp_edges.push_back(tmp); if (edge_code[tmp] < id) id = edge_code[tmp]; } while (tmp != e); for (int i = 0; i < tmp_edges.size(); i++) ans.insert(make_pair(tmp_edges[i], id)); } //case (2) if (parent[u] != 0 && low[v] >= dfn[u]) { points++; int tmp = -1, id = kMaxM; vector<int> tmp_edges; do{ tmp = stk.top(); stk.pop(); tmp_edges.push_back(tmp); if (edge_code[tmp] < id) id = edge_code[tmp]; } while (tmp != e); for (int i = 0; i < tmp_edges.size(); i++) ans.insert(make_pair(tmp_edges[i], id)); } } //节点v已访问,则(u,v)为回边 else if (v != parent[u]) { stk.push(e); low[u] = min(low[u], dfn[v]); } } } int main() { scanf("%d %d", &n, &m); graph.resize(n + 1); int u, v,tmp; for (int i = 1; i <= m; i++) { scanf("%d %d", &u, &v); graph[u].push_back(v); graph[v].push_back(u); tmp = HashEdge(u, v); edges.push_back(tmp); edge_code.insert(make_pair(tmp, i)); } dfs(1); //求解最后一个连通分量 int max_tmp = kMaxM; for (int i = 1; i <= m; i++) { if (ans.find(edges[i – 1]) == ans.end()) if (edge_code[edges[i – 1]] < max_tmp) max_tmp = edge_code[edges[i – 1]]; } printf("%dn", points + 1); for (int i = 1; i <= m; i++) printf("%d ", ans[edges[i – 1]] == 0 ? max_tmp : ans[edges[i – 1]]); return 0; } [/cpp] 本代码提交AC,用时240MS,内存10MB。]]>
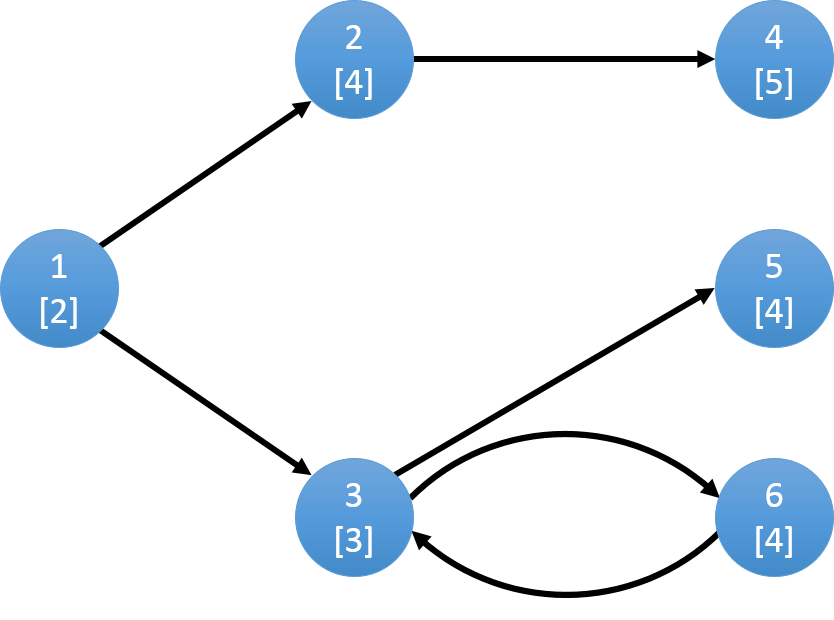 图中每个点表示一个草场,上部分数字表示编号,下部分表示草场的牧草数量w。
在1吃完草之后,小Hi和小Ho可以选择把牛羊群赶到2或者3,假设小Hi和小Ho把牛羊群赶到2:
吃完草场2之后,只能到草场4,当4吃完后没有可以到达的草场,所以小Hi和小Ho就把牛羊群赶回家。
若选择从1到3,则可以到达5,6:
选择5的话,吃完之后只能直接回家。若选择6,还可以再通过6回到3,再到5。
所以该图可以选择的路线有3条:
1->2->4 total: 11
1->3->5 total: 9
1->3->6->3->5 total: 13
所以最多能够吃到的牧草数量为13。
本题改编自USACO月赛金组
提示:强连通分量
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2行:N个正整数,第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000
第3..M+2行:2个正整数,u,v。表示存在一条从u到v的单向路径。1≤u,v≤N
输出
第1行:1个整数,最多能够吃到的牧草数量。
样例输入
6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3
样例输出
13
图中每个点表示一个草场,上部分数字表示编号,下部分表示草场的牧草数量w。
在1吃完草之后,小Hi和小Ho可以选择把牛羊群赶到2或者3,假设小Hi和小Ho把牛羊群赶到2:
吃完草场2之后,只能到草场4,当4吃完后没有可以到达的草场,所以小Hi和小Ho就把牛羊群赶回家。
若选择从1到3,则可以到达5,6:
选择5的话,吃完之后只能直接回家。若选择6,还可以再通过6回到3,再到5。
所以该图可以选择的路线有3条:
1->2->4 total: 11
1->3->5 total: 9
1->3->6->3->5 total: 13
所以最多能够吃到的牧草数量为13。
本题改编自USACO月赛金组
提示:强连通分量
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2行:N个正整数,第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000
第3..M+2行:2个正整数,u,v。表示存在一条从u到v的单向路径。1≤u,v≤N
输出
第1行:1个整数,最多能够吃到的牧草数量。
样例输入
6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3
样例输出
13
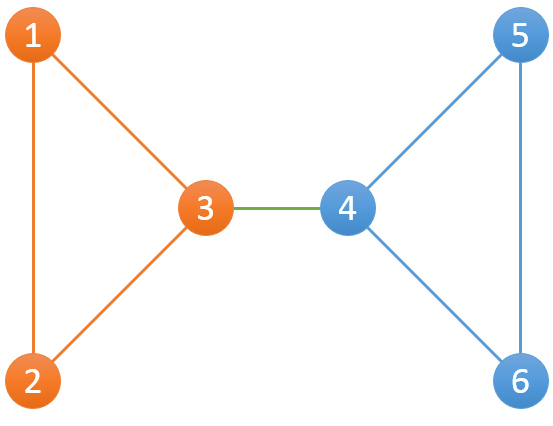
 其中包含2个组,分别为{1,2,3},{4,5,6}。对{1,2,3}而言,当1-2断开后,仍然有1-3-2可以连接1和2;当2-3断开后,仍然有2-1-3可以连接2和3;当1-3断开后,仍然有1-2-3可以连接1和3。{4,5,6}这组也是一样。
其中包含2个组,分别为{1,2,3},{4,5,6}。对{1,2,3}而言,当1-2断开后,仍然有1-3-2可以连接1和2;当2-3断开后,仍然有2-1-3可以连接2和3;当1-3断开后,仍然有1-2-3可以连接1和3。{4,5,6}这组也是一样。
 老师把整个网络的情况告诉了小Hi和小Ho,小Hi和小Ho要计算出每一台服务器的分组信息。
提示:边的双连通分量
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:1个整数,表示该网络的服务器组数。
第2行:N个整数,第i个数表示第i个服务器所属组内,编号最小的服务器的编号。比如分为{1,2,3},{4,5,6},则输出{1,1,1,4,4,4};若分为{1,4,5},{2,3,6}则输出{1,2,2,1,1,2}
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
2
1 1 1 4 4 4
老师把整个网络的情况告诉了小Hi和小Ho,小Hi和小Ho要计算出每一台服务器的分组信息。
提示:边的双连通分量
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:1个整数,表示该网络的服务器组数。
第2行:N个整数,第i个数表示第i个服务器所属组内,编号最小的服务器的编号。比如分为{1,2,3},{4,5,6},则输出{1,1,1,4,4,4};若分为{1,4,5},{2,3,6}则输出{1,2,2,1,1,2}
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
2
1 1 1 4 4 4
 ]]>
]]>
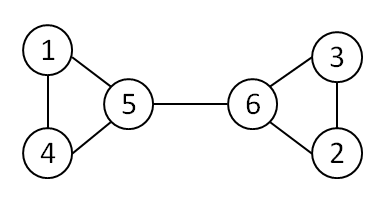
 每两个点之间至少有一条路径连通,当切断边(3,4)的时候,可以发现,整个网络被隔离为{1,2,3},{4,5,6}两个部分:
每两个点之间至少有一条路径连通,当切断边(3,4)的时候,可以发现,整个网络被隔离为{1,2,3},{4,5,6}两个部分:
 若关闭服务器3,则整个网络被隔离为{1,2},{4,5,6}两个部分:
若关闭服务器3,则整个网络被隔离为{1,2},{4,5,6}两个部分:
 小Hi和小Ho想要知道,在学校的网络中有哪些连接和哪些点被关闭后,能够使得整个网络被隔离为两个部分。
在上面的例子中,满足条件的有边(3,4),点3和点4。
提示:割边&割点
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:若干整数,用空格隔开,表示满足要求的服务器编号。从小到大排列。若没有满足要求的点,该行输出Null
第2..k行:每行2个整数,(u,v)表示满足要求的边,u<v。所有边根据u的大小排序,u小的排在前,当u相同时,v小的排在前面。若没有满足要求的边,则不输出
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3 4
3 4
小Hi和小Ho想要知道,在学校的网络中有哪些连接和哪些点被关闭后,能够使得整个网络被隔离为两个部分。
在上面的例子中,满足条件的有边(3,4),点3和点4。
提示:割边&割点
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:若干整数,用空格隔开,表示满足要求的服务器编号。从小到大排列。若没有满足要求的点,该行输出Null
第2..k行:每行2个整数,(u,v)表示满足要求的边,u<v。所有边根据u的大小排序,u小的排在前,当u相同时,v小的排在前面。若没有满足要求的边,则不输出
样例输入
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
样例输出
3 4
3 4
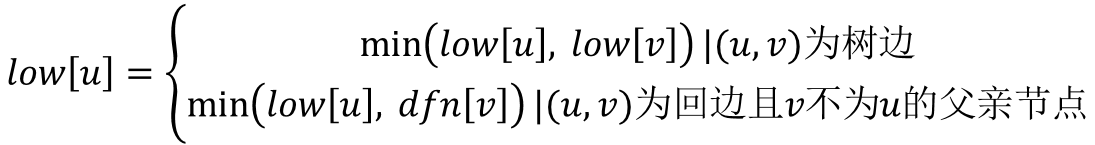 主要要理解上面的递推公式。首先理解dfn和low的含义,dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)。
上图的第一个式子,当(u,v)为树边时,low[u]表明u能追溯到的最早节点,low[v]表明u的子树(v就是u的子树的根)能追溯到的最早节点,所以根据low[u]的定义有low[u]=min(low[u],low[v])。
上图的第二个式子,当(u,v)为回边时,因为low[u]的定义就是u通过非父子边(回边)追溯最早的节点,所以既然(u,v)为回边,自然的low[u]=min(low[u],dfn[v])。
另外注意输出格式,点要从小到大排列;边(u,v)保证u<v,以u从小到大排列,再以v从小到大排列。完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<set>
#include<algorithm>
#include<vector>
using namespace std;
const int kMaxN = 20005;
int n, m;
typedef struct edge
{
int x, y;
bool operator<(const edge& p)const//如果要加入到set中,需要重载<
{
return (this->x<p.x) || ((this->x == p.x) && (this->y<p.y));
}
};
set<int> points;
set<edge> edges;
vector<vector<int>> graph;
int visit[kMaxN];
int dfn[kMaxN];
int low[kMaxN];
int parent[kMaxN];
void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;
//记录节点u的子树数
int children = 0;
visit[u] = 1;
//初始化dfn与low
dfn[u] = low[u] = ++counter;
for (int i = 0; i < graph[u].size();i++) {
int v = graph[u][i];
//节点v未被访问,则(u,v)为树边
if (visit[v]==0) {
children++;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if (parent[u] == 0 && children > 1) {
points.insert(u);
}
//case (2)
if (parent[u] != 0 && low[v] >= dfn[u]) {
points.insert(u);
}
//bridge
if (low[v] > dfn[u]) {
edge e;
e.x = u;
e.y = v;
if (u > v)
{
e.x = v;
e.y = u;
}
edges.insert(e);
}
}
//节点v已访问,则(u,v)为回边
else if (v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
scanf("%d %d", &n, &m);
graph.resize(n + 1);
int u, v;
while (m–)
{
scanf("%d %d", &u, &v);
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(1);
if (points.size() == 0)
printf("Null\n");
else
{
set<int>::iterator it = points.begin();
while (it != points.end())
{
printf("%d ", *it);
it++;
}
printf("\n");
}
if (edges.size() > 0)
{
set<edge>::iterator it = edges.begin();
while (it != edges.end())
{
printf("%d %d\n", (*it).x, (*it).y);
it++;
}
}
return 0;
}
[/cpp]
本代码提交AC,用时76MS,内存7MB。]]>
主要要理解上面的递推公式。首先理解dfn和low的含义,dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)。
上图的第一个式子,当(u,v)为树边时,low[u]表明u能追溯到的最早节点,low[v]表明u的子树(v就是u的子树的根)能追溯到的最早节点,所以根据low[u]的定义有low[u]=min(low[u],low[v])。
上图的第二个式子,当(u,v)为回边时,因为low[u]的定义就是u通过非父子边(回边)追溯最早的节点,所以既然(u,v)为回边,自然的low[u]=min(low[u],dfn[v])。
另外注意输出格式,点要从小到大排列;边(u,v)保证u<v,以u从小到大排列,再以v从小到大排列。完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<set>
#include<algorithm>
#include<vector>
using namespace std;
const int kMaxN = 20005;
int n, m;
typedef struct edge
{
int x, y;
bool operator<(const edge& p)const//如果要加入到set中,需要重载<
{
return (this->x<p.x) || ((this->x == p.x) && (this->y<p.y));
}
};
set<int> points;
set<edge> edges;
vector<vector<int>> graph;
int visit[kMaxN];
int dfn[kMaxN];
int low[kMaxN];
int parent[kMaxN];
void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;
//记录节点u的子树数
int children = 0;
visit[u] = 1;
//初始化dfn与low
dfn[u] = low[u] = ++counter;
for (int i = 0; i < graph[u].size();i++) {
int v = graph[u][i];
//节点v未被访问,则(u,v)为树边
if (visit[v]==0) {
children++;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if (parent[u] == 0 && children > 1) {
points.insert(u);
}
//case (2)
if (parent[u] != 0 && low[v] >= dfn[u]) {
points.insert(u);
}
//bridge
if (low[v] > dfn[u]) {
edge e;
e.x = u;
e.y = v;
if (u > v)
{
e.x = v;
e.y = u;
}
edges.insert(e);
}
}
//节点v已访问,则(u,v)为回边
else if (v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
scanf("%d %d", &n, &m);
graph.resize(n + 1);
int u, v;
while (m–)
{
scanf("%d %d", &u, &v);
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(1);
if (points.size() == 0)
printf("Null\n");
else
{
set<int>::iterator it = points.begin();
while (it != points.end())
{
printf("%d ", *it);
it++;
}
printf("\n");
}
if (edges.size() > 0)
{
set<edge>::iterator it = edges.begin();
while (it != edges.end())
{
printf("%d %d\n", (*it).x, (*it).y);
it++;
}
}
return 0;
}
[/cpp]
本代码提交AC,用时76MS,内存7MB。]]>