POJ 3070-Fibonacci
Fibonacci
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 26421 | Accepted: 17616 |
Description
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
An alternative formula for the Fibonacci sequence is
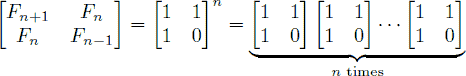
.
Given an integer n, your goal is to compute the last 4 digits of Fn.
Input
The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.
Output
For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).
Sample Input
0 9 999999999 1000000000 -1
Sample Output
0 34 626 6875
Hint
As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by
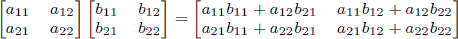
.
Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:
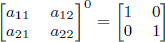
.
SourceStanford Local 2006
斐波那契数列是这样一个数列:0,1,1,2,3,5…,其数学定义为:
$$\begin{equation}f(n)=\begin{cases} 0, & n=0;\ 1, & n=1;\ f(n-1)+f(n-2), & n>1.\end{cases}\end{equation}$$
最简单的递归解法为:
typedef long long LL;
LL Fib1(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
return Fib1(n – 1) + Fib1(n – 2);
}这种算法的时间复杂度是 $O(2^n)$。 但是这种解法有很多重复计算,比如算f(8)=f(7)+f(6)时,f(7)重复计算了f(6)。所以我们可以从小开始算起,把f(n)的前两个值保存下来,每次滚动赋值,代码如下:
LL Fib2(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
LL fn_2 = 0, fn_1 = 1, ans = 0;
for (int i = 2; i <= n; ++i) {
ans = fn_1 + fn_2;
fn_2 = fn_1;
fn_1 = ans;
}
return ans;
}这种算法的时间复杂度是 $O(n)$。 最近遇到快速幂相关的题,发现求解斐波那契数列也可以用快速幂来求解,时间复杂度居然能降到 $O(lg(n))$。
题目的图中给出了斐波那契数列的矩阵形式,f(n)为矩阵[1,1;1,0]的n次幂的第一行第二个数。可以用归纳法证明。矩阵的n次幂和数的n次幂都可以用快速幂来求解,时间复杂度能降到 $O(lg(n))$。 代码如下:
const int MAXN = 2;
vector<vector<LL> > multi(const vector<vector<LL> >& mat1, const vector<vector<LL> >& mat2)
{
vector<vector<LL> > mat(MAXN, vector<LL>(MAXN, 0));
for (int i = 0; i < MAXN; ++i) {
for (int j = 0; j < MAXN; ++j) {
for (int k = 0; k < MAXN; ++k) {
mat[i][j] += mat1[i][k] * mat2[k][j];
}
}
}
return mat;
}
vector<vector<LL> > fastPow(vector<vector<LL> >& mat1, int n)
{
vector<vector<LL> > mat(MAXN, vector<LL>(MAXN, 0));
for (int i = 0; i < MAXN; ++i)
mat[i][i] = 1;
while (n != 0) {
if (n & 1)
mat = multi(mat, mat1);
mat1 = multi(mat1, mat1);
n >>= 1;
}
return mat;
}
LL Fib3(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
vector<vector<LL> > mat = { { 1, 1 }, { 1, 0 } };
vector<vector<LL> > matN = fastPow(mat, n);
return matN[0][1];
}POJ这题的代码如下,古老的POJ居然不支持第37行的vector初始化,崩溃。
#include <iostream> #include<cstdio>
#include <vector>
using namespace std;
typedef long long LL;
const int MAXN = 2;
const int MOD = 10000;
vector<vector<LL> > multi(const vector<vector<LL> >& mat1, const vector<vector<LL> >& mat2)
{
vector<vector<LL> > mat(MAXN, vector<LL>(MAXN, 0));
for (int i = 0; i < MAXN; ++i) {
for (int j = 0; j < MAXN; ++j) {
for (int k = 0; k < MAXN; ++k) {
mat[i][j] = (mat[i][j] + mat1[i][k] * mat2[k][j]) % MOD;
}
}
}
return mat;
}
vector<vector<LL> > fastPow(vector<vector<LL> >& mat1, int n)
{
vector<vector<LL> > mat(MAXN, vector<LL>(MAXN, 0));
for (int i = 0; i < MAXN; ++i)
mat[i][i] = 1;
while (n != 0) {
if (n & 1)
mat = multi(mat, mat1);
mat1 = multi(mat1, mat1);
n >>= 1;
}
return mat;
}
LL Fib3(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
//vector<vector<LL>> mat = { { 1,1 },{ 1,0 } }; //———————–
vector<vector<LL> > mat;
vector<LL> r1;
r1.push_back(1), r1.push_back(1);
vector<LL> r2;
r2.push_back(1), r2.push_back(0);
mat.push_back(r1);
mat.push_back(r2); //———————-
vector<vector<LL> > matN = fastPow(mat, n);
return matN[0][1];
}
int main()
{
int n;
while (scanf("%d", &n) && n != -1) {
LL ans = Fib3(n);
printf("%d\n", ans % MOD);
}
return 0;
}本代码提交AC,用时32MS,真的好快呀。
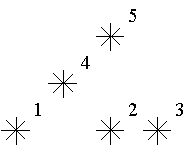 For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it’s formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
You are to write a program that will count the amounts of the stars of each level on a given map.
Input
The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.
Output
The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.
Sample Input
5
1 1
5 1
7 1
3 3
5 5
Sample Output
1
2
1
1
Hint
This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.
Source
Ural Collegiate Programming Contest 1999
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it’s formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
You are to write a program that will count the amounts of the stars of each level on a given map.
Input
The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.
Output
The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.
Sample Input
5
1 1
5 1
7 1
3 3
5 5
Sample Output
1
2
1
1
Hint
This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.
Source
Ural Collegiate Programming Contest 1999
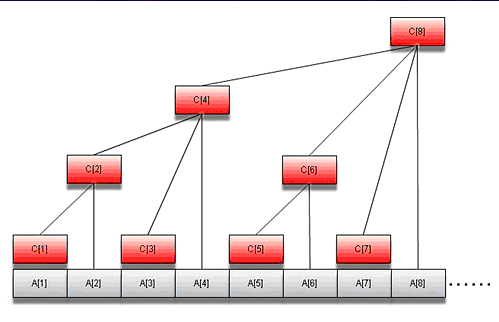 树状数组[1][/caption]当来了一个横坐标为4的星星之后,其level正是A[1]+…+A[4]=C[4],在树状数组中正好是其左下方的和。
关于树状数组可以参考[1]的文章。
所以横坐标为4的星星的level就是sum(4)。当又来了一个横坐标为4的星星之后,需要修改A[4],使A[4]++,其实就是A[4]+1,可以使用add(4,1)操作。
因为本题中x可能等于0,但是树状数组中下标从1开始,所以需要整体将x+1。本题是树状数组的一个简单应用,完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
using namespace std;
const int kMaxN = 32005;//NOT 15005;
int n;
int level[kMaxN];
int c[kMaxN];
int lowbit(int x)
{
return x&(-x);
}
int sum(int i)
{
int rs = 0;
while (i > 0)
{
rs += c[i];
i -= lowbit(i);
}
return rs;
}
void add(int i, int val)
{
while (i <= kMaxN)
{
c[i]+=val;
i += lowbit(i);
}
}
int main()
{
scanf("%d", &n);
int x, y;
for (int i = 0; i < n; i++)
{
scanf("%d %d", &x, &y);
x++;
level[sum(x)]++;
add(x, 1);
}
for (int i = 0; i < n; i++)
printf("%dn", level[i]);
return 0;
}
[/cpp]
本代码提交AC,用时188MS,内存344K。
参考:
[1].
树状数组[1][/caption]当来了一个横坐标为4的星星之后,其level正是A[1]+…+A[4]=C[4],在树状数组中正好是其左下方的和。
关于树状数组可以参考[1]的文章。
所以横坐标为4的星星的level就是sum(4)。当又来了一个横坐标为4的星星之后,需要修改A[4],使A[4]++,其实就是A[4]+1,可以使用add(4,1)操作。
因为本题中x可能等于0,但是树状数组中下标从1开始,所以需要整体将x+1。本题是树状数组的一个简单应用,完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
using namespace std;
const int kMaxN = 32005;//NOT 15005;
int n;
int level[kMaxN];
int c[kMaxN];
int lowbit(int x)
{
return x&(-x);
}
int sum(int i)
{
int rs = 0;
while (i > 0)
{
rs += c[i];
i -= lowbit(i);
}
return rs;
}
void add(int i, int val)
{
while (i <= kMaxN)
{
c[i]+=val;
i += lowbit(i);
}
}
int main()
{
scanf("%d", &n);
int x, y;
for (int i = 0; i < n; i++)
{
scanf("%d %d", &x, &y);
x++;
level[sum(x)]++;
add(x, 1);
}
for (int i = 0; i < n; i++)
printf("%dn", level[i]);
return 0;
}
[/cpp]
本代码提交AC,用时188MS,内存344K。
参考:
[1].  设利用扩展欧几里得算法求到的式(3)的解为$$k_0$$和$$t_0$$,那么式(2)的解为$$k=(b/d)k_0$$,$$t=(b/d)t_0$$。那么最小的k是多少呢?
又因为根据数论中的
设利用扩展欧几里得算法求到的式(3)的解为$$k_0$$和$$t_0$$,那么式(2)的解为$$k=(b/d)k_0$$,$$t=(b/d)t_0$$。那么最小的k是多少呢?
又因为根据数论中的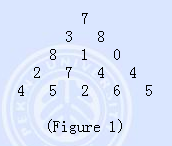 Figure 1 shows a number triangle. Write a program that calculates the highest sum of numbers passed on a route that starts at the top and ends somewhere on the base. Each step can go either diagonally down to the left or diagonally down to the right.
Input
Your program is to read from standard input. The first line contains one integer N: the number of rows in the triangle. The following N lines describe the data of the triangle. The number of rows in the triangle is > 1 but <= 100. The numbers in the triangle, all integers, are between 0 and 99.
Output
Your program is to write to standard output. The highest sum is written as an integer.
Sample Input
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30
Source
IOI 1994
Figure 1 shows a number triangle. Write a program that calculates the highest sum of numbers passed on a route that starts at the top and ends somewhere on the base. Each step can go either diagonally down to the left or diagonally down to the right.
Input
Your program is to read from standard input. The first line contains one integer N: the number of rows in the triangle. The following N lines describe the data of the triangle. The number of rows in the triangle is > 1 but <= 100. The numbers in the triangle, all integers, are between 0 and 99.
Output
Your program is to write to standard output. The highest sum is written as an integer.
Sample Input
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30
Source
IOI 1994
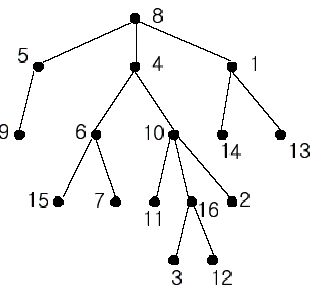 In the figure, each node is labeled with an integer from {1, 2,…,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,…, N. Each of the next N -1 lines contains a pair of integers that represent an edge –the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N – 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
Source
Taejon 2002
In the figure, each node is labeled with an integer from {1, 2,…,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,…, N. Each of the next N -1 lines contains a pair of integers that represent an edge –the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N – 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
Source
Taejon 2002
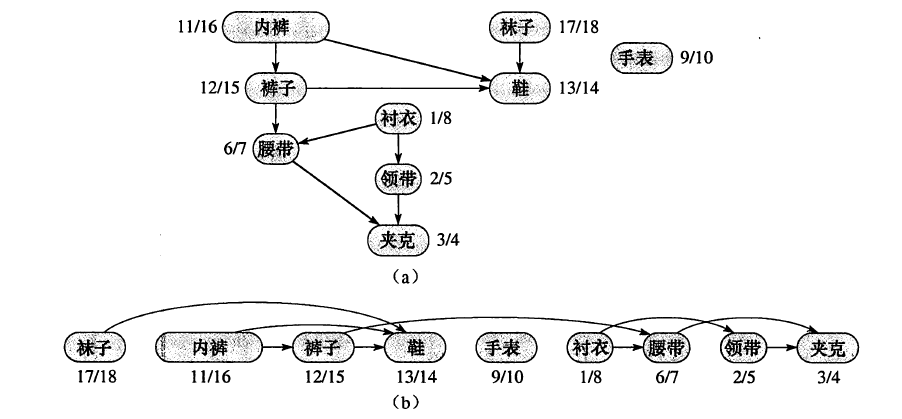 如上图是《算法导论》中关于拓扑排序的一个例子,这是某位教授起床后需要穿戴衣物的顺序,比如只有先穿了袜子才能穿鞋、但是穿鞋和戴手表并没有严格的先后顺序。拓扑排序的功能就是根据图(a)的拓扑图,得到图(b)中节点的先后顺序。
常见的拓扑排序算法有两种:Kahn算法和基于DFS的算法,这两种算法都很好理解,详细的解释请看维基百科
如上图是《算法导论》中关于拓扑排序的一个例子,这是某位教授起床后需要穿戴衣物的顺序,比如只有先穿了袜子才能穿鞋、但是穿鞋和戴手表并没有严格的先后顺序。拓扑排序的功能就是根据图(a)的拓扑图,得到图(b)中节点的先后顺序。
常见的拓扑排序算法有两种:Kahn算法和基于DFS的算法,这两种算法都很好理解,详细的解释请看维基百科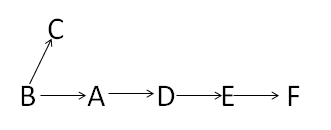 那么怎么判断生产的拓扑序列是否是严格的有序序列呢?基本原则就是就是任意取序列中的两个点,看能不能比较大小,如果能则是严格有序,否则不是。
我起初想到的是对拓扑序列的第一个节点进行深度遍历,遍历之后如果所有的节点都访问了,那么这是一个严格有序的序列,否则不是。后来证明这是不正确的,比如上图从B点开始DFS,遍历完F之后回溯到B点再访问C点,这样即使它不是严格有序的,但DFS还是访问了所有节点。
后来想到了Floyd算法。对拓扑图进行Floyd算法之后,会得到任意两点之间的最短距离。如果拓扑序列中前面的节点都可以到达后面的节点(最短距离不为无穷),则是严格有序的;否则不是。比如上图的一个拓扑序列为BCADEF(不唯一,还可以是BADEFC),但是C到ADEF的最短距离都是无穷,所以这个序列不是严格有序的。
把这些大的问题搞清楚之后就可以写代码了,一些小细节可以看我代码里的注释。
[cpp]
#include<iostream>
//#include<set>
#include<list>
#include<string>
#include<vector>
using namespace std;
int n,m;
const int MAX_N=26;
const int MAX_DIS=10000;
//*******这些都是维基百科关于拓扑排序(DFS版)里的变量含义
int temporary[MAX_N];
int permanent[MAX_N];
int marked[MAX_N];
//*******************************
int path[MAX_N][MAX_N];
//int dfs_visited[MAX_N];
list<int> L;//拓扑排序生产的顺序链
bool isDAG;//DAG=directed acyclic graph,无回路有向图
//每一个测试用例都要初始化路径
void init_path()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
path[i][j]=0;
}
//每一次拓扑排序都要初始化temporary,permanent,marked
void init_tpm()
{
isDAG=true;
L.clear();
for(int i=0;i<n;i++)
{
temporary[i]=0;
permanent[i]=0;
marked[i]=0;
}
}
//递归访问。具体看维基百科
void visit(int i)
{
if(temporary[i]==1)
{
isDAG=false;
return;
}
else
{
if(marked[i]==0)
{
marked[i]=1;
temporary[i]=1;
for(int j=0;j<n;j++)
{
if(path[i][j]==1)
{
visit(j);
}
}
permanent[i]=1;
temporary[i]=0;
L.push_front(i);
}
}
}
/*
void init_dfs()
{
for(int i=0;i<n;i++)
dfs_visited[i]=0;
}*/
/*
//DFS有缺陷
void DFS(int v)
{
if(dfs_visited[v]==0)
{
dfs_visited[v]=1;
for(int i=0;i<n;i++)
{
if(dfs_visited[i]==0&&path[v][i]==1)
{
DFS(i);
}
}
}
}*/
//使用Floyd算法来判断生产的拓扑排序是否是严格有序的
bool Floyd()
{
int copy_path[MAX_N][MAX_N];
for(int i=0;i<n;i++)//首先复制一份路径图
for(int j=0;j<n;j++)
{
copy_path[i][j]=path[i][j];
if(i!=j&©_path[i][j]==0)//如果原来两点距离为0,说明他们是不直接连通的
copy_path[i][j]=MAX_DIS;//置为无穷
}
//floyd算法
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) if(copy_path[i][j]>copy_path[i][k]+copy_path[k][j])
copy_path[i][j]=copy_path[i][k]+copy_path[k][j];
vector<int> seq;//把原来用链表的拓扑序列转换成数组,方便后面的操作
list<int>::iterator it=L.begin();
while(it!=L.end())
{
seq.push_back(*it);
it++;
}
//如果这个拓扑链是严格有序的话,则前面的元素到后面的元素一定是可达的。
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++) { if(copy_path[seq[i]][seq[j]]>=MAX_DIS)//如果不可达,则不是严格有序的。
return false;
}
}
return true;
}
//拓扑排序DFS版本。返回0:有回路;1:虽然是拓扑排序,但非连通(不是严格有序);2:是拓扑排序且连通(严格有序)(即任意两个元素都可以比较大小)
int topological_sorting()
{
for(int i=0;i<n;i++)
{
if(marked[i]==0)
{
visit(i);
}
}
if(!isDAG)
return 0;
else
{
/*init_dfs();
DFS(*L.begin());
for(int i=0;i<n;i++) { if(dfs_visited[i]==0) { return 1; } }*/ if(Floyd()) return 2; else return 1; } } int main() { //freopen("input.txt","r",stdin); string tmp; while(cin>>n>>m&&n&&m)
{
init_path();
vector<string> relations(m);
int i;
for(i=0;i<m;i++)//一次性把所有输入都存起来,免得后续麻烦 { cin>>relations[i];
}
int rs=-1;
for(i=0;i<m;i++)//每增加一个关系,都要重新拓扑排序一次
{
init_tpm();//每次都要初始化
tmp=relations[i];
path[tmp[0]-‘A’][tmp[2]-‘A’]=1;
rs=topological_sorting();
if(rs==0)
{
cout<<"Inconsistency found after "<<i+1<<" relations."<<endl;
break;//如果是回路的话,后续的输入可以跳过
}
else if(rs==2)//成功
{
cout<<"Sorted sequence determined after "<<i+1<<" relations: ";
list<int>::iterator it=L.begin();
while(it!=L.end())
{
char c=’A’+*it;
cout<<c;
it++;
}
cout<<"."<<endl;
break;//后续输入跳过
}
}
if(i==m&&rs==1)//如果处理完所有输入都没有形成严格有序的拓扑序列
cout<<"Sorted sequence cannot be determined."<<endl;
}
return 0;
}
[/cpp]
我原本以为又是DFS,又是Floyd,算法时空效率会很低,但是提交后AC,用时125MS,内存244K,也不是很差。
代码中的拓扑排序算法使用的是基于DFS的版本,大家也可以改成Kahn算法。
如果觉得自己的代码是对的,但是提交WA的,可以使用这两个测试数据:
那么怎么判断生产的拓扑序列是否是严格的有序序列呢?基本原则就是就是任意取序列中的两个点,看能不能比较大小,如果能则是严格有序,否则不是。
我起初想到的是对拓扑序列的第一个节点进行深度遍历,遍历之后如果所有的节点都访问了,那么这是一个严格有序的序列,否则不是。后来证明这是不正确的,比如上图从B点开始DFS,遍历完F之后回溯到B点再访问C点,这样即使它不是严格有序的,但DFS还是访问了所有节点。
后来想到了Floyd算法。对拓扑图进行Floyd算法之后,会得到任意两点之间的最短距离。如果拓扑序列中前面的节点都可以到达后面的节点(最短距离不为无穷),则是严格有序的;否则不是。比如上图的一个拓扑序列为BCADEF(不唯一,还可以是BADEFC),但是C到ADEF的最短距离都是无穷,所以这个序列不是严格有序的。
把这些大的问题搞清楚之后就可以写代码了,一些小细节可以看我代码里的注释。
[cpp]
#include<iostream>
//#include<set>
#include<list>
#include<string>
#include<vector>
using namespace std;
int n,m;
const int MAX_N=26;
const int MAX_DIS=10000;
//*******这些都是维基百科关于拓扑排序(DFS版)里的变量含义
int temporary[MAX_N];
int permanent[MAX_N];
int marked[MAX_N];
//*******************************
int path[MAX_N][MAX_N];
//int dfs_visited[MAX_N];
list<int> L;//拓扑排序生产的顺序链
bool isDAG;//DAG=directed acyclic graph,无回路有向图
//每一个测试用例都要初始化路径
void init_path()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
path[i][j]=0;
}
//每一次拓扑排序都要初始化temporary,permanent,marked
void init_tpm()
{
isDAG=true;
L.clear();
for(int i=0;i<n;i++)
{
temporary[i]=0;
permanent[i]=0;
marked[i]=0;
}
}
//递归访问。具体看维基百科
void visit(int i)
{
if(temporary[i]==1)
{
isDAG=false;
return;
}
else
{
if(marked[i]==0)
{
marked[i]=1;
temporary[i]=1;
for(int j=0;j<n;j++)
{
if(path[i][j]==1)
{
visit(j);
}
}
permanent[i]=1;
temporary[i]=0;
L.push_front(i);
}
}
}
/*
void init_dfs()
{
for(int i=0;i<n;i++)
dfs_visited[i]=0;
}*/
/*
//DFS有缺陷
void DFS(int v)
{
if(dfs_visited[v]==0)
{
dfs_visited[v]=1;
for(int i=0;i<n;i++)
{
if(dfs_visited[i]==0&&path[v][i]==1)
{
DFS(i);
}
}
}
}*/
//使用Floyd算法来判断生产的拓扑排序是否是严格有序的
bool Floyd()
{
int copy_path[MAX_N][MAX_N];
for(int i=0;i<n;i++)//首先复制一份路径图
for(int j=0;j<n;j++)
{
copy_path[i][j]=path[i][j];
if(i!=j&©_path[i][j]==0)//如果原来两点距离为0,说明他们是不直接连通的
copy_path[i][j]=MAX_DIS;//置为无穷
}
//floyd算法
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) if(copy_path[i][j]>copy_path[i][k]+copy_path[k][j])
copy_path[i][j]=copy_path[i][k]+copy_path[k][j];
vector<int> seq;//把原来用链表的拓扑序列转换成数组,方便后面的操作
list<int>::iterator it=L.begin();
while(it!=L.end())
{
seq.push_back(*it);
it++;
}
//如果这个拓扑链是严格有序的话,则前面的元素到后面的元素一定是可达的。
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++) { if(copy_path[seq[i]][seq[j]]>=MAX_DIS)//如果不可达,则不是严格有序的。
return false;
}
}
return true;
}
//拓扑排序DFS版本。返回0:有回路;1:虽然是拓扑排序,但非连通(不是严格有序);2:是拓扑排序且连通(严格有序)(即任意两个元素都可以比较大小)
int topological_sorting()
{
for(int i=0;i<n;i++)
{
if(marked[i]==0)
{
visit(i);
}
}
if(!isDAG)
return 0;
else
{
/*init_dfs();
DFS(*L.begin());
for(int i=0;i<n;i++) { if(dfs_visited[i]==0) { return 1; } }*/ if(Floyd()) return 2; else return 1; } } int main() { //freopen("input.txt","r",stdin); string tmp; while(cin>>n>>m&&n&&m)
{
init_path();
vector<string> relations(m);
int i;
for(i=0;i<m;i++)//一次性把所有输入都存起来,免得后续麻烦 { cin>>relations[i];
}
int rs=-1;
for(i=0;i<m;i++)//每增加一个关系,都要重新拓扑排序一次
{
init_tpm();//每次都要初始化
tmp=relations[i];
path[tmp[0]-‘A’][tmp[2]-‘A’]=1;
rs=topological_sorting();
if(rs==0)
{
cout<<"Inconsistency found after "<<i+1<<" relations."<<endl;
break;//如果是回路的话,后续的输入可以跳过
}
else if(rs==2)//成功
{
cout<<"Sorted sequence determined after "<<i+1<<" relations: ";
list<int>::iterator it=L.begin();
while(it!=L.end())
{
char c=’A’+*it;
cout<<c;
it++;
}
cout<<"."<<endl;
break;//后续输入跳过
}
}
if(i==m&&rs==1)//如果处理完所有输入都没有形成严格有序的拓扑序列
cout<<"Sorted sequence cannot be determined."<<endl;
}
return 0;
}
[/cpp]
我原本以为又是DFS,又是Floyd,算法时空效率会很低,但是提交后AC,用时125MS,内存244K,也不是很差。
代码中的拓扑排序算法使用的是基于DFS的版本,大家也可以改成Kahn算法。
如果觉得自己的代码是对的,但是提交WA的,可以使用这两个测试数据: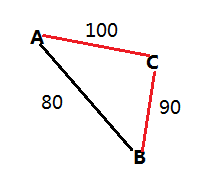 如上图所示,假设要从A到B,在用Floyd算法时,判断要不要借助C点,如果不借助,则load_ton[A][B]=80;如果借助C点,则路径变为A->C->B,A->C最多能载100吨,C->B最多能载90吨,所以总的来说,A->C->B最多能载min{100,90}=90吨;而90>80,所以借助C点后的载重大于不借助C点的载重,所以修改load_ton[A][B]=90。
知道这一点,我们可以很快的写出代码:
[cpp]
#include<iostream>
#include<map>
#include<string>
using namespace std;
const int MAX_N=202;
int load_ton[MAX_N][MAX_N];
//初始化数据
void init_load(int n)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
load_ton[i][j]=0;
}
//改造Floyd算法
void Floyd(int n)
{
for(int k=0;k<n;k++)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
int min_ton=load_ton[i][k]<load_ton[k][j]?load_ton[i][k]:load_ton[k][j];//这条路上的最小值即为能通过的最大值
if(load_ton[i][j]<min_ton)
{
load_ton[i][j]=min_ton;//对称矩阵
load_ton[j][i]=min_ton;//对称矩阵
}
}
}
}
}
int main()
{
//freopen("input.txt","r",stdin);
int n,r;
int case_num=1;
while(cin>>n>>r&&n&&r)
{
init_load(n);
map<string,int> city_index;//保存城市和下标的对应关系
string city1,city2;
int w;
int i=0;
while(r–)
{
cin>>city1>>city2>>w;
if(city_index.find(city1)==city_index.end())
city_index[city1]=i++;
if(city_index.find(city2)==city_index.end())
city_index[city2]=i++;
//load_ton[i-2][i-1]=w;//错,因为有可能cityi在之前已经加入了,这个时候i-1,i-2就不是cityi的下标了
//load_ton[i-1][i-2]=w;
load_ton[city_index[city1]][city_index[city2]]=w;//还是要从map里找对应下标
load_ton[city_index[city2]][city_index[city1]]=w;//因为路是两边通的,所以a[i][j]和a[j][i]相等
}
cin>>city1>>city2;
Floyd(n);
cout<<"Scenario #"<<case_num++<<endl;//
cout<<load_ton[city_index[city1]][city_index[city2]]<<" tons"<<endl<<endl;
}
return 0;
}
[/cpp]
本代码提交AC,用时79MS,内存316K。
在写代码的时候有几个小细节需要注意。在输入数据的时候,用MAP来保存城市和下标的关系,方便后面Floyd算法的操作;因为道路是双向通行的,所以保存数据时要保存成对称矩阵。
]]>
如上图所示,假设要从A到B,在用Floyd算法时,判断要不要借助C点,如果不借助,则load_ton[A][B]=80;如果借助C点,则路径变为A->C->B,A->C最多能载100吨,C->B最多能载90吨,所以总的来说,A->C->B最多能载min{100,90}=90吨;而90>80,所以借助C点后的载重大于不借助C点的载重,所以修改load_ton[A][B]=90。
知道这一点,我们可以很快的写出代码:
[cpp]
#include<iostream>
#include<map>
#include<string>
using namespace std;
const int MAX_N=202;
int load_ton[MAX_N][MAX_N];
//初始化数据
void init_load(int n)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
load_ton[i][j]=0;
}
//改造Floyd算法
void Floyd(int n)
{
for(int k=0;k<n;k++)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
int min_ton=load_ton[i][k]<load_ton[k][j]?load_ton[i][k]:load_ton[k][j];//这条路上的最小值即为能通过的最大值
if(load_ton[i][j]<min_ton)
{
load_ton[i][j]=min_ton;//对称矩阵
load_ton[j][i]=min_ton;//对称矩阵
}
}
}
}
}
int main()
{
//freopen("input.txt","r",stdin);
int n,r;
int case_num=1;
while(cin>>n>>r&&n&&r)
{
init_load(n);
map<string,int> city_index;//保存城市和下标的对应关系
string city1,city2;
int w;
int i=0;
while(r–)
{
cin>>city1>>city2>>w;
if(city_index.find(city1)==city_index.end())
city_index[city1]=i++;
if(city_index.find(city2)==city_index.end())
city_index[city2]=i++;
//load_ton[i-2][i-1]=w;//错,因为有可能cityi在之前已经加入了,这个时候i-1,i-2就不是cityi的下标了
//load_ton[i-1][i-2]=w;
load_ton[city_index[city1]][city_index[city2]]=w;//还是要从map里找对应下标
load_ton[city_index[city2]][city_index[city1]]=w;//因为路是两边通的,所以a[i][j]和a[j][i]相等
}
cin>>city1>>city2;
Floyd(n);
cout<<"Scenario #"<<case_num++<<endl;//
cout<<load_ton[city_index[city1]][city_index[city2]]<<" tons"<<endl<<endl;
}
return 0;
}
[/cpp]
本代码提交AC,用时79MS,内存316K。
在写代码的时候有几个小细节需要注意。在输入数据的时候,用MAP来保存城市和下标的关系,方便后面Floyd算法的操作;因为道路是双向通行的,所以保存数据时要保存成对称矩阵。
]]>