POJ 1330-Nearest Common Ancestors
Nearest Common Ancestors
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 19432 Accepted: 10292
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
In the figure, each node is labeled with an integer from {1, 2,…,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,…, N. Each of the next N -1 lines contains a pair of integers that represent an edge –the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N – 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
Source
Taejon 2002
昨天被hihoCoder Problem 1067: 最近公共祖先·二的离线算法虐了之后，今天在POJ上找了一个水题来重塑信心，这个题也是最近公共祖先问题，只不过它是目前为止最简单的，和hihoCoder Problem 1062: 最近公共祖先·一类似，甚至更简单，因为这个题每个case只询问一次，所以没必要用离线算法，而且给的就是数字，不是字符串，连转换都不要。直接记录一个节点node1的所有祖先，然后从下往上查找另一个节点node2的所有祖先，每找到一个祖先，则判断这个祖先是否是node1的祖先，如果是，则这就是他们的公共祖先。 这一次我甚至连set和map都没有用，因为给定的是连续的整数，直接用数组当hash即可，而且查找效率比set和map还快。 完整代码如下： [cpp] #include<iostream> #include<vector> using namespace std; int main() { //freopen("input.txt","r",stdin); int t,n; int node1,node2; cin>>t; while(t–) { cin>>n; vector<int> s_f(n+1,0);//s_f[i]为第i个节点的父亲，开始时所有节点的父亲为0 for(int i=0;i<n-1;i++) { cin>>node1>>node2; s_f[node2]=node1;//保存输入关系 } cin>>node1>>node2; vector<int> node1_father(n+1,0);//node1的父亲 node1_father[node1]=1;//自己是自己的祖先 while(s_f[node1]!=0) { node1_father[s_f[node1]]=1;//记录哪些点是node1的父亲 node1=s_f[node1]; } if(node1_father[node2]!=0)//node2也是自己的祖先 { cout<<node2<<endl; continue; } while(s_f[node2]!=0) { if(node1_father[s_f[node2]]!=0)//从下网上找node2的祖先是否出现在node1的祖先里 { cout<<s_f[node2]<<endl; break; } else node2=s_f[node2]; } } return 0; } [/cpp] 本代码提交AC，用时125MS，内存336K。 关于最近公共祖先问题，还有一种牛逼的在线算法RMQ，在hihoCoder上也有提到，下回再战！]]>
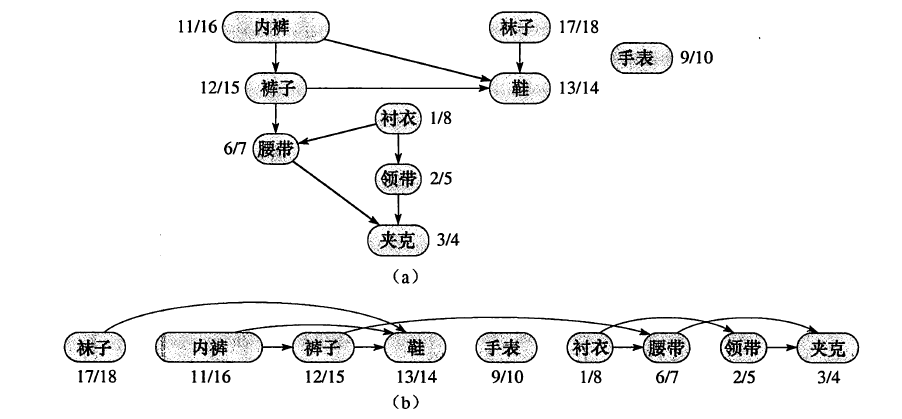如上图是《算法导论》中关于拓扑排序的一个例子，这是某位教授起床后需要穿戴衣物的顺序，比如只有先穿了袜子才能穿鞋、但是穿鞋和戴手表并没有严格的先后顺序。拓扑排序的功能就是根据图(a)的拓扑图，得到图(b)中节点的先后顺序。
常见的拓扑排序算法有两种：Kahn算法和基于DFS的算法，这两种算法都很好理解，详细的解释请看维基百科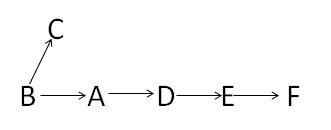
那么怎么判断生产的拓扑序列是否是严格的有序序列呢？基本原则就是就是任意取序列中的两个点，看能不能比较大小，如果能则是严格有序，否则不是。
我起初想到的是对拓扑序列的第一个节点进行深度遍历，遍历之后如果所有的节点都访问了，那么这是一个严格有序的序列，否则不是。后来证明这是不正确的，比如上图从B点开始DFS，遍历完F之后回溯到B点再访问C点，这样即使它不是严格有序的，但DFS还是访问了所有节点。
后来想到了Floyd算法。对拓扑图进行Floyd算法之后，会得到任意两点之间的最短距离。如果拓扑序列中前面的节点都可以到达后面的节点（最短距离不为无穷），则是严格有序的；否则不是。比如上图的一个拓扑序列为BCADEF（不唯一，还可以是BADEFC），但是C到ADEF的最短距离都是无穷，所以这个序列不是严格有序的。
把这些大的问题搞清楚之后就可以写代码了，一些小细节可以看我代码里的注释。
[cpp]
#include<iostream>
//#include<set>
#include<list>
#include<string>
#include<vector>
using namespace std;
int n,m;
const int MAX_N=26;
const int MAX_DIS=10000;
//*******这些都是维基百科关于拓扑排序（DFS版）里的变量含义
int temporary[MAX_N];
int permanent[MAX_N];
int marked[MAX_N];
//*******************************
int path[MAX_N][MAX_N];
//int dfs_visited[MAX_N];
list<int> L;//拓扑排序生产的顺序链
bool isDAG;//DAG=directed acyclic graph，无回路有向图
//每一个测试用例都要初始化路径
void init_path()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
path[i][j]=0;
}
//每一次拓扑排序都要初始化temporary，permanent，marked
void init_tpm()
{
isDAG=true;
L.clear();
for(int i=0;i<n;i++)
{
temporary[i]=0;
permanent[i]=0;
marked[i]=0;
}
}
//递归访问。具体看维基百科
void visit(int i)
{
if(temporary[i]==1)
{
isDAG=false;
return;
}
else
{
if(marked[i]==0)
{
marked[i]=1;
temporary[i]=1;
for(int j=0;j<n;j++)
{
if(path[i][j]==1)
{
visit(j);
}
}
permanent[i]=1;
temporary[i]=0;
L.push_front(i);
}
}
}
/*
void init_dfs()
{
for(int i=0;i<n;i++)
dfs_visited[i]=0;
}*/
/*
//DFS有缺陷
void DFS(int v)
{
if(dfs_visited[v]==0)
{
dfs_visited[v]=1;
for(int i=0;i<n;i++)
{
if(dfs_visited[i]==0&&path[v][i]==1)
{
DFS(i);
}
}
}
}*/
//使用Floyd算法来判断生产的拓扑排序是否是严格有序的
bool Floyd()
{
int copy_path[MAX_N][MAX_N];
for(int i=0;i<n;i++)//首先复制一份路径图
for(int j=0;j<n;j++)
{
copy_path[i][j]=path[i][j];
if(i!=j&©_path[i][j]==0)//如果原来两点距离为0，说明他们是不直接连通的
copy_path[i][j]=MAX_DIS;//置为无穷
}
//floyd算法
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) if(copy_path[i][j]>copy_path[i][k]+copy_path[k][j])
copy_path[i][j]=copy_path[i][k]+copy_path[k][j];
vector<int> seq;//把原来用链表的拓扑序列转换成数组，方便后面的操作
list<int>::iterator it=L.begin();
while(it!=L.end())
{
seq.push_back(*it);
it++;
}
//如果这个拓扑链是严格有序的话，则前面的元素到后面的元素一定是可达的。
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++) { if(copy_path[seq[i]][seq[j]]>=MAX_DIS)//如果不可达，则不是严格有序的。
return false;
}
}
return true;
}
//拓扑排序DFS版本。返回0：有回路；1：虽然是拓扑排序，但非连通（不是严格有序）；2：是拓扑排序且连通（严格有序）（即任意两个元素都可以比较大小）
int topological_sorting()
{
for(int i=0;i<n;i++)
{
if(marked[i]==0)
{
visit(i);
}
}
if(!isDAG)
return 0;
else
{
/*init_dfs();
DFS(*L.begin());
for(int i=0;i<n;i++) { if(dfs_visited[i]==0) { return 1; } }*/ if(Floyd()) return 2; else return 1; } } int main() { //freopen("input.txt","r",stdin); string tmp; while(cin>>n>>m&&n&&m)
{
init_path();
vector<string> relations(m);
int i;
for(i=0;i<m;i++)//一次性把所有输入都存起来，免得后续麻烦 { cin>>relations[i];
}
int rs=-1;
for(i=0;i<m;i++)//每增加一个关系，都要重新拓扑排序一次
{
init_tpm();//每次都要初始化
tmp=relations[i];
path[tmp[0]-‘A’][tmp[2]-‘A’]=1;
rs=topological_sorting();
if(rs==0)
{
cout<<"Inconsistency found after "<<i+1<<" relations."<<endl;
break;//如果是回路的话，后续的输入可以跳过
}
else if(rs==2)//成功
{
cout<<"Sorted sequence determined after "<<i+1<<" relations: ";
list<int>::iterator it=L.begin();
while(it!=L.end())
{
char c=’A’+*it;
cout<<c;
it++;
}
cout<<"."<<endl;
break;//后续输入跳过
}
}
if(i==m&&rs==1)//如果处理完所有输入都没有形成严格有序的拓扑序列
cout<<"Sorted sequence cannot be determined."<<endl;
}
return 0;
}
[/cpp]
我原本以为又是DFS，又是Floyd，算法时空效率会很低，但是提交后AC，用时125MS，内存244K，也不是很差。
代码中的拓扑排序算法使用的是基于DFS的版本，大家也可以改成Kahn算法。
如果觉得自己的代码是对的，但是提交WA的，可以使用这两个测试数据：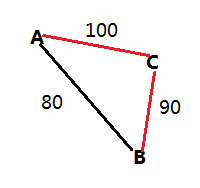
如上图所示，假设要从A到B，在用Floyd算法时，判断要不要借助C点，如果不借助，则load_ton[A][B]=80；如果借助C点，则路径变为A->C->B，A->C最多能载100吨，C->B最多能载90吨，所以总的来说，A->C->B最多能载min{100,90}=90吨；而90>80，所以借助C点后的载重大于不借助C点的载重，所以修改load_ton[A][B]=90。
知道这一点，我们可以很快的写出代码：
[cpp]
#include<iostream>
#include<map>
#include<string>
using namespace std;
const int MAX_N=202;
int load_ton[MAX_N][MAX_N];
//初始化数据
void init_load(int n)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
load_ton[i][j]=0;
}
//改造Floyd算法
void Floyd(int n)
{
for(int k=0;k<n;k++)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
int min_ton=load_ton[i][k]<load_ton[k][j]?load_ton[i][k]:load_ton[k][j];//这条路上的最小值即为能通过的最大值
if(load_ton[i][j]<min_ton)
{
load_ton[i][j]=min_ton;//对称矩阵
load_ton[j][i]=min_ton;//对称矩阵
}
}
}
}
}
int main()
{
//freopen("input.txt","r",stdin);
int n,r;
int case_num=1;
while(cin>>n>>r&&n&&r)
{
init_load(n);
map<string,int> city_index;//保存城市和下标的对应关系
string city1,city2;
int w;
int i=0;
while(r–)
{
cin>>city1>>city2>>w;
if(city_index.find(city1)==city_index.end())
city_index[city1]=i++;
if(city_index.find(city2)==city_index.end())
city_index[city2]=i++;
//load_ton[i-2][i-1]=w;//错，因为有可能cityi在之前已经加入了，这个时候i-1,i-2就不是cityi的下标了
//load_ton[i-1][i-2]=w;
load_ton[city_index[city1]][city_index[city2]]=w;//还是要从map里找对应下标
load_ton[city_index[city2]][city_index[city1]]=w;//因为路是两边通的，所以a[i][j]和a[j][i]相等
}
cin>>city1>>city2;
Floyd(n);
cout<<"Scenario #"<<case_num++<<endl;//
cout<<load_ton[city_index[city1]][city_index[city2]]<<" tons"<<endl<<endl;
}
return 0;
}
[/cpp]
本代码提交AC，用时79MS，内存316K。
在写代码的时候有几个小细节需要注意。在输入数据的时候，用MAP来保存城市和下标的关系，方便后面Floyd算法的操作；因为道路是双向通行的，所以保存数据时要保存成对称矩阵。
]]>
如果op_i=0，说明这两个人是同一个集合的，即他们有共同的祖先，则首先判断这两个人在不在map中，如果不在，则以自身为祖先加入到map中，然后执行UNION操作把他们合并为一个集合。
如果op_i=1，要判断两个人是否在一个集合中，想当然的FIND他们的祖先，如果祖先相同，说明他们是一个集合的。
理清了上述关系，马上写出代码：
[cpp]
#include<iostream>
#include<string>
#include<map>
using namespace std;
map<string,string> represent;
//并查集FIND操作
string find_represent(string name)
{
if(name==represent[name])
return name;
else
{
represent[name]=find_represent(represent[name]);//把经过的节点全部链接到根节点
return represent[name];
}
}
int main()
{
//freopen("input.txt","r",stdin);
int n;
int op;
string name1,name2;
cin>>n;
while(n–)
{
cin>>op>>name1>>name2;
if(op==0)
{
if(represent.find(name1)==represent.end())
represent[name1]=name1;
if(represent.find(name2)==represent.end())
represent[name2]=name2;
represent[find_represent(name1)]=find_represent(name2);//UNION操作
}
else
{
//**********也需要先判断是否在map里*********
if(represent.find(name1)==represent.end())
represent[name1]=name1;
if(represent.find(name2)==represent.end())
represent[name2]=name2;
//******************************************
if(find_represent(name1)==find_represent(name2))
cout<<"yes"<<endl;
else
cout<<"no"<<endl;
}
}
return 0;
}
[/cpp]
本代码提交AC，用时243MS，内存1MB。
需要注意的是，由于本题使用MAP实现，在执行FIND操作时有这么一句：
[cpp]
if(name==represent[name])
[/cpp]
对于STL的map，如果本来map中不存在a这个元素，执行了if(map[a]==”sth”)之后，也会自动把a加入map，最后就是map[a]=””，为空。虽然就某一次来说，这样判断的结果和下面修正的结果是一样的，但是如果下一次op_i=0需要加入a时发现map中已经有a了，就直接执行UNION操作了，但是这个时候a的祖先却是空””，而本来a的祖先应该是它自己a的。所以这就会对后面的结果产生影响。所以当我们op_i=1时，如果某个人不在map中，我们也要把它加入map并使其祖先为自身。
关于这道题，