POJ 1094-Sorting It All Out Sorting It All Out Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 28397 Accepted: 9814 Description An ascending sorted sequence of distinct values is one in which some form of a less-than operator is used to order the elements from smallest to largest. For example, the sorted sequence A, B, C, D implies that A < B, B < C and C < D. in this problem, we will give you a set of relations of the form A < B and ask you to determine whether a sorted order has been specified or not. Input Input consists of multiple problem instances. Each instance starts with a line containing two positive integers n and m. the first value indicated the number of objects to sort, where 2 <= n <= 26. The objects to be sorted will be the first n characters of the uppercase alphabet. The second value m indicates the number of relations of the form A < B which will be given in this problem instance. Next will be m lines, each containing one such relation consisting of three characters: an uppercase letter, the character “<” and a second uppercase letter. No letter will be outside the range of the first n letters of the alphabet. Values of n = m = 0 indicate end of input. Output For each problem instance, output consists of one line. This line should be one of the following three: Sorted sequence determined after xxx relations: yyy…y. Sorted sequence cannot be determined. Inconsistency found after xxx relations. where xxx is the number of relations processed at the time either a sorted sequence is determined or an inconsistency is found, whichever comes first, and yyy…y is the sorted, ascending sequence. Sample Input 4 6 A<B A<C B<C C<D B<D A<B 3 2 A<B B<A 26 1 A<Z 0 0 Sample Output Sorted sequence determined after 4 relations: ABCD. Inconsistency found after 2 relations. Sorted sequence cannot be determined. Source East Central North America 2001
这一题有一定的难度,有很多细节需要兼顾。题目的意思为:给定一系列小于关系,问能否从中得出一个严格有序的序列。需要明确的是,题目所指的严格有序的序列需要满足如下几个条件:1.包含n个所有字母;2.每个字母都有明确的大小关系。 另外根据测试样例我们可以知道:每输入一个关系都要判断一次,如果可以得到严格有序序列,则输出结果,但这个测试用例后续的输入还是要输入的;如果出现相互依赖(环),也输出结果,同样的,这个测试用例后面的数据还是要输入;如果所有关系都输入了还不能得出一个严格有序的序列,则输入无法判断。 这一题很自然的想到用拓扑排序来做。下面我们先来回顾一下拓扑排序。
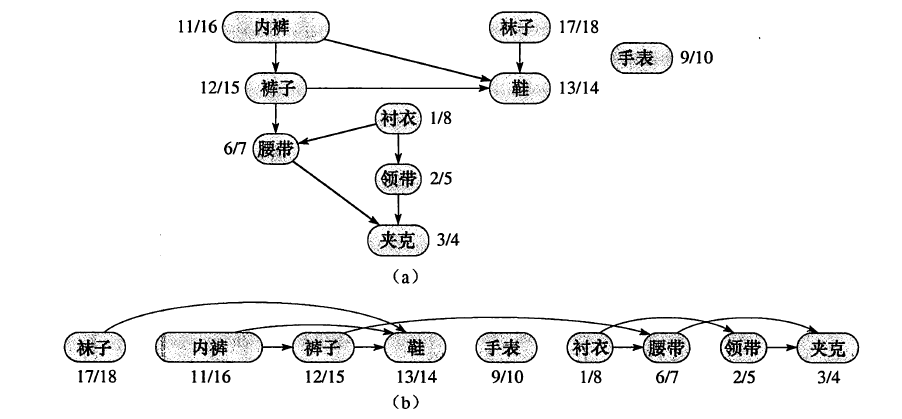 如上图是《算法导论》中关于拓扑排序的一个例子,这是某位教授起床后需要穿戴衣物的顺序,比如只有先穿了袜子才能穿鞋、但是穿鞋和戴手表并没有严格的先后顺序。拓扑排序的功能就是根据图(a)的拓扑图,得到图(b)中节点的先后顺序。
常见的拓扑排序算法有两种:Kahn算法和基于DFS的算法,这两种算法都很好理解,详细的解释请看维基百科Topological sorting,下面简要介绍一下这两个算法。
Kahn算法
拓扑排序强调先后顺序,先做的事情排在前面,那么反应到有向图上,最先做的事情就是没有入度的节点(可能 有/没有 出度)。所以Kahn算法很朴素,他就是把所有没有入度的点加入到集合S中,在S不为空的情况下循环:从S中取出一个节点a,把a加入到L链表的尾部,对于每一条a的出度边,如< a,b>,删除它,并把b的入度减一,如果b的入度也为0了,则又把b加入到集合S中。如果S为空了,但是图中还有边未删除,说明图中至少有一个环,拓扑排序失败;否则拓扑排序成功,且链表L保存了一条拓扑排序链。(链表L的生成使用尾插法)
维基百科上关于Kahn算法的伪代码描述如下:
[cpp]
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
add n to tail of L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
[/cpp]
基于DFS的算法
这个算法类似于深度优先搜索,它不断的递归访问下一个节点,直到不能再递归时,把最后一个节点插入到链表的头部,然后返回。
拿上面穿衣物的例子来说,如果我们首先选择了内裤,则可以递归访问裤子->腰带->夹克。到夹克时,无法递归了,则把夹克插入到L的头部,返回到腰带,腰带也无法递归了,则把腰带插入到L的头部,这个时候就形成了L:腰带->夹克的中间结果,也就是腰带要在夹克前面穿。这个算法不太好表述,还请大家看伪代码领会。(链表L的生成使用头插法)
[cpp]
L ← Empty list that will contain the sorted nodes
while there are unmarked nodes do
select an unmarked node n
visit(n)
function visit(node n)
if n has a temporary mark then stop (not a DAG)
if n is not marked (i.e. has not been visited yet) then
mark n temporarily
for each node m with an edge from n to m do
visit(m)
mark n permanently
unmark n temporarily
add n to head of L
[/cpp]
那么问题来了,只使用拓扑排序并不能满足本题的要求。因为本题问的是能否生成一个严格有序的序列,一个拓扑序列并不一定是严格有序的序列,比如上图中的穿衣物生成的拓扑序列中,先穿袜子和先穿衬衫都是可以的,也就是说袜子和衬衫是没有明确的先后顺序的,所以这不是一个严格有序的序列。再比如下图的拓扑序列,也不是一个严格有序的序列,因为C和A,D,E,F无法比较大小。
如上图是《算法导论》中关于拓扑排序的一个例子,这是某位教授起床后需要穿戴衣物的顺序,比如只有先穿了袜子才能穿鞋、但是穿鞋和戴手表并没有严格的先后顺序。拓扑排序的功能就是根据图(a)的拓扑图,得到图(b)中节点的先后顺序。
常见的拓扑排序算法有两种:Kahn算法和基于DFS的算法,这两种算法都很好理解,详细的解释请看维基百科Topological sorting,下面简要介绍一下这两个算法。
Kahn算法
拓扑排序强调先后顺序,先做的事情排在前面,那么反应到有向图上,最先做的事情就是没有入度的节点(可能 有/没有 出度)。所以Kahn算法很朴素,他就是把所有没有入度的点加入到集合S中,在S不为空的情况下循环:从S中取出一个节点a,把a加入到L链表的尾部,对于每一条a的出度边,如< a,b>,删除它,并把b的入度减一,如果b的入度也为0了,则又把b加入到集合S中。如果S为空了,但是图中还有边未删除,说明图中至少有一个环,拓扑排序失败;否则拓扑排序成功,且链表L保存了一条拓扑排序链。(链表L的生成使用尾插法)
维基百科上关于Kahn算法的伪代码描述如下:
[cpp]
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
add n to tail of L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
[/cpp]
基于DFS的算法
这个算法类似于深度优先搜索,它不断的递归访问下一个节点,直到不能再递归时,把最后一个节点插入到链表的头部,然后返回。
拿上面穿衣物的例子来说,如果我们首先选择了内裤,则可以递归访问裤子->腰带->夹克。到夹克时,无法递归了,则把夹克插入到L的头部,返回到腰带,腰带也无法递归了,则把腰带插入到L的头部,这个时候就形成了L:腰带->夹克的中间结果,也就是腰带要在夹克前面穿。这个算法不太好表述,还请大家看伪代码领会。(链表L的生成使用头插法)
[cpp]
L ← Empty list that will contain the sorted nodes
while there are unmarked nodes do
select an unmarked node n
visit(n)
function visit(node n)
if n has a temporary mark then stop (not a DAG)
if n is not marked (i.e. has not been visited yet) then
mark n temporarily
for each node m with an edge from n to m do
visit(m)
mark n permanently
unmark n temporarily
add n to head of L
[/cpp]
那么问题来了,只使用拓扑排序并不能满足本题的要求。因为本题问的是能否生成一个严格有序的序列,一个拓扑序列并不一定是严格有序的序列,比如上图中的穿衣物生成的拓扑序列中,先穿袜子和先穿衬衫都是可以的,也就是说袜子和衬衫是没有明确的先后顺序的,所以这不是一个严格有序的序列。再比如下图的拓扑序列,也不是一个严格有序的序列,因为C和A,D,E,F无法比较大小。
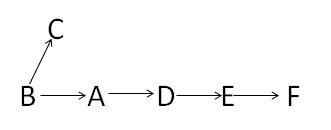 那么怎么判断生产的拓扑序列是否是严格的有序序列呢?基本原则就是就是任意取序列中的两个点,看能不能比较大小,如果能则是严格有序,否则不是。
我起初想到的是对拓扑序列的第一个节点进行深度遍历,遍历之后如果所有的节点都访问了,那么这是一个严格有序的序列,否则不是。后来证明这是不正确的,比如上图从B点开始DFS,遍历完F之后回溯到B点再访问C点,这样即使它不是严格有序的,但DFS还是访问了所有节点。
后来想到了Floyd算法。对拓扑图进行Floyd算法之后,会得到任意两点之间的最短距离。如果拓扑序列中前面的节点都可以到达后面的节点(最短距离不为无穷),则是严格有序的;否则不是。比如上图的一个拓扑序列为BCADEF(不唯一,还可以是BADEFC),但是C到ADEF的最短距离都是无穷,所以这个序列不是严格有序的。
把这些大的问题搞清楚之后就可以写代码了,一些小细节可以看我代码里的注释。
[cpp]
#include<iostream>
//#include<set>
#include<list>
#include<string>
#include<vector>
using namespace std;
int n,m;
const int MAX_N=26;
const int MAX_DIS=10000;
//*******这些都是维基百科关于拓扑排序(DFS版)里的变量含义
int temporary[MAX_N];
int permanent[MAX_N];
int marked[MAX_N];
//*******************************
int path[MAX_N][MAX_N];
//int dfs_visited[MAX_N];
list<int> L;//拓扑排序生产的顺序链
bool isDAG;//DAG=directed acyclic graph,无回路有向图
//每一个测试用例都要初始化路径
void init_path()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
path[i][j]=0;
}
//每一次拓扑排序都要初始化temporary,permanent,marked
void init_tpm()
{
isDAG=true;
L.clear();
for(int i=0;i<n;i++)
{
temporary[i]=0;
permanent[i]=0;
marked[i]=0;
}
}
//递归访问。具体看维基百科
void visit(int i)
{
if(temporary[i]==1)
{
isDAG=false;
return;
}
else
{
if(marked[i]==0)
{
marked[i]=1;
temporary[i]=1;
for(int j=0;j<n;j++)
{
if(path[i][j]==1)
{
visit(j);
}
}
permanent[i]=1;
temporary[i]=0;
L.push_front(i);
}
}
}
/*
void init_dfs()
{
for(int i=0;i<n;i++)
dfs_visited[i]=0;
}*/
/*
//DFS有缺陷
void DFS(int v)
{
if(dfs_visited[v]==0)
{
dfs_visited[v]=1;
for(int i=0;i<n;i++)
{
if(dfs_visited[i]==0&&path[v][i]==1)
{
DFS(i);
}
}
}
}*/
//使用Floyd算法来判断生产的拓扑排序是否是严格有序的
bool Floyd()
{
int copy_path[MAX_N][MAX_N];
for(int i=0;i<n;i++)//首先复制一份路径图
for(int j=0;j<n;j++)
{
copy_path[i][j]=path[i][j];
if(i!=j&©_path[i][j]==0)//如果原来两点距离为0,说明他们是不直接连通的
copy_path[i][j]=MAX_DIS;//置为无穷
}
//floyd算法
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) if(copy_path[i][j]>copy_path[i][k]+copy_path[k][j])
copy_path[i][j]=copy_path[i][k]+copy_path[k][j];
vector<int> seq;//把原来用链表的拓扑序列转换成数组,方便后面的操作
list<int>::iterator it=L.begin();
while(it!=L.end())
{
seq.push_back(*it);
it++;
}
//如果这个拓扑链是严格有序的话,则前面的元素到后面的元素一定是可达的。
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++) { if(copy_path[seq[i]][seq[j]]>=MAX_DIS)//如果不可达,则不是严格有序的。
return false;
}
}
return true;
}
//拓扑排序DFS版本。返回0:有回路;1:虽然是拓扑排序,但非连通(不是严格有序);2:是拓扑排序且连通(严格有序)(即任意两个元素都可以比较大小)
int topological_sorting()
{
for(int i=0;i<n;i++)
{
if(marked[i]==0)
{
visit(i);
}
}
if(!isDAG)
return 0;
else
{
/*init_dfs();
DFS(*L.begin());
for(int i=0;i<n;i++) { if(dfs_visited[i]==0) { return 1; } }*/ if(Floyd()) return 2; else return 1; } } int main() { //freopen("input.txt","r",stdin); string tmp; while(cin>>n>>m&&n&&m)
{
init_path();
vector<string> relations(m);
int i;
for(i=0;i<m;i++)//一次性把所有输入都存起来,免得后续麻烦 { cin>>relations[i];
}
int rs=-1;
for(i=0;i<m;i++)//每增加一个关系,都要重新拓扑排序一次
{
init_tpm();//每次都要初始化
tmp=relations[i];
path[tmp[0]-‘A’][tmp[2]-‘A’]=1;
rs=topological_sorting();
if(rs==0)
{
cout<<"Inconsistency found after "<<i+1<<" relations."<<endl;
break;//如果是回路的话,后续的输入可以跳过
}
else if(rs==2)//成功
{
cout<<"Sorted sequence determined after "<<i+1<<" relations: ";
list<int>::iterator it=L.begin();
while(it!=L.end())
{
char c=’A’+*it;
cout<<c;
it++;
}
cout<<"."<<endl;
break;//后续输入跳过
}
}
if(i==m&&rs==1)//如果处理完所有输入都没有形成严格有序的拓扑序列
cout<<"Sorted sequence cannot be determined."<<endl;
}
return 0;
}
[/cpp]
我原本以为又是DFS,又是Floyd,算法时空效率会很低,但是提交后AC,用时125MS,内存244K,也不是很差。
代码中的拓扑排序算法使用的是基于DFS的版本,大家也可以改成Kahn算法。
如果觉得自己的代码是对的,但是提交WA的,可以使用这两个测试数据:数据1,数据2。
]]>
那么怎么判断生产的拓扑序列是否是严格的有序序列呢?基本原则就是就是任意取序列中的两个点,看能不能比较大小,如果能则是严格有序,否则不是。
我起初想到的是对拓扑序列的第一个节点进行深度遍历,遍历之后如果所有的节点都访问了,那么这是一个严格有序的序列,否则不是。后来证明这是不正确的,比如上图从B点开始DFS,遍历完F之后回溯到B点再访问C点,这样即使它不是严格有序的,但DFS还是访问了所有节点。
后来想到了Floyd算法。对拓扑图进行Floyd算法之后,会得到任意两点之间的最短距离。如果拓扑序列中前面的节点都可以到达后面的节点(最短距离不为无穷),则是严格有序的;否则不是。比如上图的一个拓扑序列为BCADEF(不唯一,还可以是BADEFC),但是C到ADEF的最短距离都是无穷,所以这个序列不是严格有序的。
把这些大的问题搞清楚之后就可以写代码了,一些小细节可以看我代码里的注释。
[cpp]
#include<iostream>
//#include<set>
#include<list>
#include<string>
#include<vector>
using namespace std;
int n,m;
const int MAX_N=26;
const int MAX_DIS=10000;
//*******这些都是维基百科关于拓扑排序(DFS版)里的变量含义
int temporary[MAX_N];
int permanent[MAX_N];
int marked[MAX_N];
//*******************************
int path[MAX_N][MAX_N];
//int dfs_visited[MAX_N];
list<int> L;//拓扑排序生产的顺序链
bool isDAG;//DAG=directed acyclic graph,无回路有向图
//每一个测试用例都要初始化路径
void init_path()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
path[i][j]=0;
}
//每一次拓扑排序都要初始化temporary,permanent,marked
void init_tpm()
{
isDAG=true;
L.clear();
for(int i=0;i<n;i++)
{
temporary[i]=0;
permanent[i]=0;
marked[i]=0;
}
}
//递归访问。具体看维基百科
void visit(int i)
{
if(temporary[i]==1)
{
isDAG=false;
return;
}
else
{
if(marked[i]==0)
{
marked[i]=1;
temporary[i]=1;
for(int j=0;j<n;j++)
{
if(path[i][j]==1)
{
visit(j);
}
}
permanent[i]=1;
temporary[i]=0;
L.push_front(i);
}
}
}
/*
void init_dfs()
{
for(int i=0;i<n;i++)
dfs_visited[i]=0;
}*/
/*
//DFS有缺陷
void DFS(int v)
{
if(dfs_visited[v]==0)
{
dfs_visited[v]=1;
for(int i=0;i<n;i++)
{
if(dfs_visited[i]==0&&path[v][i]==1)
{
DFS(i);
}
}
}
}*/
//使用Floyd算法来判断生产的拓扑排序是否是严格有序的
bool Floyd()
{
int copy_path[MAX_N][MAX_N];
for(int i=0;i<n;i++)//首先复制一份路径图
for(int j=0;j<n;j++)
{
copy_path[i][j]=path[i][j];
if(i!=j&©_path[i][j]==0)//如果原来两点距离为0,说明他们是不直接连通的
copy_path[i][j]=MAX_DIS;//置为无穷
}
//floyd算法
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) if(copy_path[i][j]>copy_path[i][k]+copy_path[k][j])
copy_path[i][j]=copy_path[i][k]+copy_path[k][j];
vector<int> seq;//把原来用链表的拓扑序列转换成数组,方便后面的操作
list<int>::iterator it=L.begin();
while(it!=L.end())
{
seq.push_back(*it);
it++;
}
//如果这个拓扑链是严格有序的话,则前面的元素到后面的元素一定是可达的。
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++) { if(copy_path[seq[i]][seq[j]]>=MAX_DIS)//如果不可达,则不是严格有序的。
return false;
}
}
return true;
}
//拓扑排序DFS版本。返回0:有回路;1:虽然是拓扑排序,但非连通(不是严格有序);2:是拓扑排序且连通(严格有序)(即任意两个元素都可以比较大小)
int topological_sorting()
{
for(int i=0;i<n;i++)
{
if(marked[i]==0)
{
visit(i);
}
}
if(!isDAG)
return 0;
else
{
/*init_dfs();
DFS(*L.begin());
for(int i=0;i<n;i++) { if(dfs_visited[i]==0) { return 1; } }*/ if(Floyd()) return 2; else return 1; } } int main() { //freopen("input.txt","r",stdin); string tmp; while(cin>>n>>m&&n&&m)
{
init_path();
vector<string> relations(m);
int i;
for(i=0;i<m;i++)//一次性把所有输入都存起来,免得后续麻烦 { cin>>relations[i];
}
int rs=-1;
for(i=0;i<m;i++)//每增加一个关系,都要重新拓扑排序一次
{
init_tpm();//每次都要初始化
tmp=relations[i];
path[tmp[0]-‘A’][tmp[2]-‘A’]=1;
rs=topological_sorting();
if(rs==0)
{
cout<<"Inconsistency found after "<<i+1<<" relations."<<endl;
break;//如果是回路的话,后续的输入可以跳过
}
else if(rs==2)//成功
{
cout<<"Sorted sequence determined after "<<i+1<<" relations: ";
list<int>::iterator it=L.begin();
while(it!=L.end())
{
char c=’A’+*it;
cout<<c;
it++;
}
cout<<"."<<endl;
break;//后续输入跳过
}
}
if(i==m&&rs==1)//如果处理完所有输入都没有形成严格有序的拓扑序列
cout<<"Sorted sequence cannot be determined."<<endl;
}
return 0;
}
[/cpp]
我原本以为又是DFS,又是Floyd,算法时空效率会很低,但是提交后AC,用时125MS,内存244K,也不是很差。
代码中的拓扑排序算法使用的是基于DFS的版本,大家也可以改成Kahn算法。
如果觉得自己的代码是对的,但是提交WA的,可以使用这两个测试数据:数据1,数据2。
]]>
Pingback: LeetCode Course Schedule | bitJoy > code