hihoCoder week 49-1-欧拉路·一 题目1 : 欧拉路·一 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 小Hi和小Ho最近在玩一个解密类的游戏，他们需要控制角色在一片原始丛林里面探险，收集道具，并找到最后的宝藏。现在他们控制的角色来到了一个很大的湖边。湖上有N个小岛(编号1..N)，以及连接小岛的M座木桥。每座木桥上各有一个宝箱，里面似乎装着什么道具。 湖边还有一个船夫，船夫告诉主角。他可以载着主角到任意一个岛上，并且可以从任意一个岛上再载着主角回到湖边，但是主角只有一次来回的机会。同时船夫告诉主角，连接岛屿之间的木桥很脆弱，走过一次之后就会断掉。 因为不知道宝箱内有什么道具，小Hi和小Ho觉得如果能把所有的道具收集齐肯定是最好的，那么对于当前岛屿和木桥的情况，能否将所有道具收集齐呢？ 举个例子，比如一个由6个小岛和8座桥组成的地图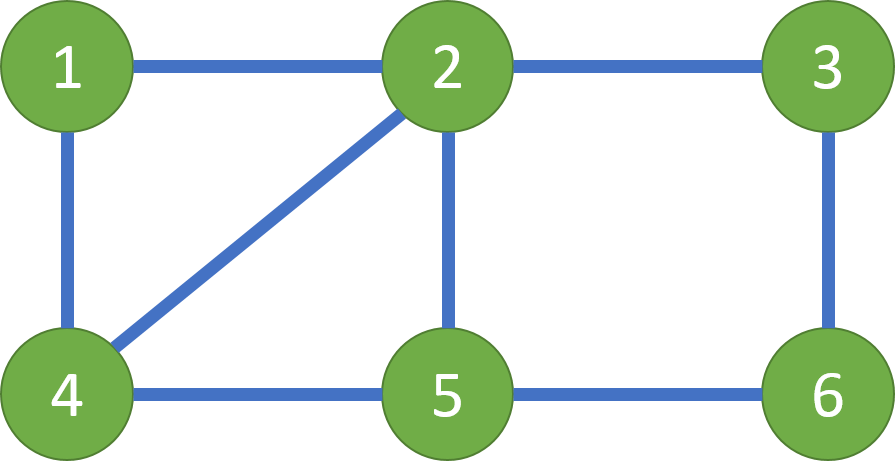： 主角可以先到达4号小岛，然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛，然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。 提示：欧拉路的判定 输入 第1行：2个正整数，N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000，1≤M≤50,000 第2..M+1行：每行2个整数，u,v。表示有一座木桥连接着编号为u和编号为v的岛屿，两个岛之间可能有多座桥。1≤u,v≤N 输出 第1行：1个字符串，如果能收集齐所有的道具输出“Full”，否则输出”Part”。 样例输入 6 8 1 2 1 4 2 4 2 5 2 3 3 6 4 5 5 6 样例输出 Full

---

本题考察无向图欧拉路的判断。 关于有向图和无向图欧拉（回）路的介绍，请看POJ Problem 1386: Play on Words。总结一下就是先用并查集判断无向图是否连通，然后判断奇数度的节点个数是否为0或2。完整代码如下： [cpp] #include<iostream> #include<cstdio> using namespace std; const int kMax = 10005; int n, m; int degree[kMax]; int father[kMax]; int Find(int x) { return x == father[x] ? x : (father[x] = Find(father[x])); } void Union(int x, int y) { father[Find(x)] = Find(y); } void Init() { for (int i = 1; i <= n; i++) father[i] = i; } bool IsConnected() { for (int i = 1; i <= n; i++) if (father[i] != father[1]) return false; return true; } bool IsEuler() { int odd = 0; for (int i = 1; i <= n; i++) if (degree[i] & 1) odd++; if (odd == 0 || odd == 2) return true; return false; } int main() { scanf("%d %d", &n, &m); int u, v; for (int i = 0; i < m; i++) { scanf("%d %d", &u, &v); degree[u]++; degree[v]++; Union(u, v); } if (IsConnected()) { if (IsEuler()) printf("Full\n"); else printf("Part\n"); } else printf("Part\n"); return 0; } [/cpp] 本代码提交AC，用时13MS，内存1MB。 总结： 判断图中是否存在环路（详细介绍可看这里） 1. 无向图：依次删除图中度数为0或1的点及其关联的边，循环结束，如果还有未删除的点，则存在回路。 2. 有向图：拓扑排序，依次删除图中入度为0的点及其关联的出边，循环结束，如果还有未删除的点，则存在回路。 判断图是否连通 1. 无向图：使用并查集，最终如果所有节点的父亲都相同，则无向图是连通的。 2. 有向图：判断有向图是否强连通貌似很复杂，Kosaraju算法、判断强连通图以及有向图强连通分量的Tarjan算法。]]>