108. Convert Sorted Array to Binary Search Tree

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

---

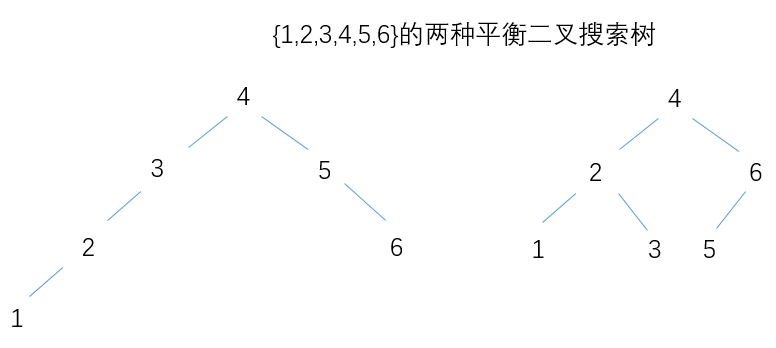
给定一个升序排列的数组，要构建一个高度平衡的二叉搜索树。 二叉搜索树的概念是递归定义的，具体可以参看维基百科，简单来说就是左孩子小于根节点，右孩子大于根节点。 但是本题要求二叉搜索树是高度平衡的，也就是说左右孩子的高度差不能大于1。 我一开始的想法是既然是平衡二叉搜索树，直接取数组中点，然后左右依次排开，肯定能得到一棵平衡二叉搜索树，如下左图所示。 但是这一版本的代码提交上去之后只通过了6个样例。后来仔细想了想，这解法未免也太简单幼稚了吧。想到之前解树的题都用到了递归，这题应该也可以用，立马灵光一闪，第一次取中点之后，递归的在左右半个数组中取中点建树，所有还可以得到如上右图所示的更加紧凑的平衡二叉搜索树。

完整代码如下：

class Solution {
public:
    TreeNode* work(vector<int>& nums, int s, int t)
    {
        if (s == t)
            return new TreeNode(nums[s]);
        if (s > t)
            return NULL;
        int mid = (s + t + 1) / 2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = work(nums, s, mid – 1);
        root->right = work(nums, mid + 1, t);
        return root;
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) { return work(nums, 0, nums.size() – 1); }
};

本代码提交AC，用时16MS。