109. Convert Sorted List to Binary Search Tree

Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

Given the sorted linked list: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

---

这一题和之前的LeetCode Convert Sorted Array to Binary Search Tree思路是一样的，只是把数组换成了链表，这样的话，就不能通过下标直接访问到中点元素了。 此时只能通过遍历找到链表的中点，然后以中点为根节点建树，最后分割左右链表，递归建树。完整代码如下：

class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head)
    {
        if (head == NULL)
            return NULL;
        if (head->next == NULL)
            return new TreeNode(head->val);
        int n = 0, cnt = 0;
        ListNode* tmp = head;
        while (tmp != NULL) {
            n++;
            tmp = tmp->next;
        }
        tmp = head;
        while (cnt < n / 2 – 1) {
            tmp = tmp->next;
            cnt++;
        } // 此时tmp是中间节点的上一个节点
        TreeNode* root = new TreeNode(tmp->next->val);
        ListNode* head2 = tmp->next->next;
        tmp->next = NULL; // 断开
        root->left = sortedListToBST(head);
        root->right = sortedListToBST(head2);
        return root;
    }
};

本代码提交AC，用时22MS。击败了87%的人:-)
后来想想这题会不会有更优的解法，网上看了一下，发现自己蠢到哭了，链表找中点居然用了这么笨的方法，之前的快慢指针都忘了。换上快慢指针找链表中点的解法如下：

class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head)
    {
        if (head == NULL)
            return NULL;
        if (head->next == NULL)
            return new TreeNode(head->val);
        ListNode *fast = head, *slow = head, *prior = head;
        while (fast->next != NULL && fast->next->next != NULL) {
            prior = slow;
            slow = slow->next;
            fast = fast->next->next;
        } // 此时slow为中间节点，prior为中间节点的上一个节点
        TreeNode* root = new TreeNode(slow->val);
        ListNode* head2 = slow->next;
        prior->next = NULL; //断开
        if (head != slow)
            root->left = sortedListToBST(head);
        root->right = sortedListToBST(head2);
        return root;
    }
};

本代码提交AC，用时26MS，有点失望，按理说这种解法是要比我上面的解法快的。
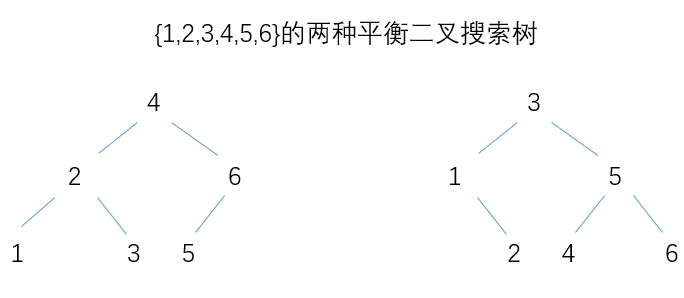
后来我又发现，这两种解法构建出来的平衡二叉搜索树不一样，如下图所示，但是他们都还算紧凑，都是正确的，看来答案不唯一啊。（其实主要是偶数长度时，有两个中间节点，选哪个都是正确的。）