LeetCode Valid Square Given the coordinates of four points in 2D space, return whether the four points could construct a square. The coordinate (x,y) of a point is represented by an integer array with two integers. Example:

Input: p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,1]
Output: True

Note:

1. All the input integers are in the range [-10000, 10000].
2. A valid square has four equal sides with positive length and four equal angles (90-degree angles).
3. Input points have no order.

---

任给平面上的四个点，问这四个点能否构成正方形。 解法1，原始几何角度。 如果要构成正方形，必须满足四条边相等，且四个角是直角。因为给定的点的顺序是不固定的，假设我们固定一个点p1，求p1到其他三个点p2,p3,p4的距离的平方len2,len3,len4，则要形成正方形，这三个距离中必定有两个距离相等，且等于另一个距离的两倍。

p3------p4
|       |
|       |
p1------p2

比如假设形成上述正方形，则有2*len2==2*len3==len4。在满足这个条件的基础上，还需要满足p1p2垂直p1p3，且p4p3垂直p4p2，且p4到p2和p3的距离相等。 当然因为点的顺序不固定，所以还有可能2*len2==2*len4==len3或者2*len3==2*len4==len2。最后需要注意的是这些点中不能由任何两个点重合，所以需要判断两点之间的距离不能为0。 完整代码如下： [cpp] class Solution2 { private: // 计算距离的平方 int distSquare(const vector<int>& p1, const vector<int>& p2) { return (p1[0] – p2[0])*(p1[0] – p2[0]) + (p1[1] – p2[1])*(p1[1] – p2[1]); } // 判断直线(p1,p2)和直线(p3,p4)是否垂直 bool isVertical(vector<int>& p1, vector<int>& p2, vector<int>& p3, vector<int>& p4) { return (p2[0] – p1[0])*(p4[0] – p3[0]) + (p2[1] – p1[1])*(p4[1] – p3[1]) == 0; } // 在2|p1p2|==2|p1p3|==|p1p4|的条件下，判断是否能形成正方形 bool helper(vector<int>& p1, vector<int>& p2, vector<int>& p3, vector<int>& p4) { if (!isVertical(p1, p2, p1, p3))return false; if (!isVertical(p4, p3, p4, p2))return false; int len2 = distSquare(p4, p2), len3 = distSquare(p4, p3); return len2 == len3; } public: bool validSquare(vector<int>& p1, vector<int>& p2, vector<int>& p3, vector<int>& p4) { int len2 = distSquare(p1, p2), len3 = distSquare(p1, p3), len4 = distSquare(p1, p4); if (len2 == 0 || len3 == 0 || len4 == 0)return false; if (len2 == len3 && 2 * len2 == len4) return helper(p1, p2, p3, p4); if (len2 == len4 && 2 * len2 == len3) return helper(p1, p2, p4, p3); if (len3 == len4 && 2 * len3 == len2) return helper(p1, p3, p4, p2); return false; } }; [/cpp] 本代码提交AC，用时6MS。 解法2，特征法。 任何一个正方形，如果求出所有点之间的距离，则这些距离只可能有两种取值，一种是邻边全相等，另一种是对角边也相等。所以我们只需要用一个map保存不同边的长度以及出现的频率即可，如果最终只有两个映射，则是正方形，否则不是。注意当出现边长为0时，说明两点重合，不能构成正方形。 代码如下： [cpp] class Solution { private: // 计算距离的平方 int distSquare(const vector<int>& p1, const vector<int>& p2) { return (p1[0] – p2[0])*(p1[0] – p2[0]) + (p1[1] – p2[1])*(p1[1] – p2[1]); } public: bool validSquare(vector<int>& p1, vector<int>& p2, vector<int>& p3, vector<int>& p4) { unordered_map<int, int> umdist; vector<vector<int>> points = { p1,p2,p3,p4 }; for (int i = 0; i < 4; ++i) { for (int j = i + 1; j < 4; ++j) { int dist = distSquare(points[i], points[j]); if (dist == 0)return false; ++umdist[dist]; } } return umdist.size() == 2; } }; [/cpp] 本代码提交AC，用时9MS。 不过上述代码有局限性，如果顶点都只是整数，则没有问题，但是如果顶点可以是实数，则会有问题。比如等边三角形的三个点和三角形的中心点，这四个点两两之间只有2种不同的距离，但他们不能构成正方形。可以再加一个限制条件，即两种不同长度的边的频率一个是4，一个是2，且出现2次的边长是出现4次的边长的两倍。 讨论区见：https://discuss.leetcode.com/topic/89985/c-3-lines-unordered_set/4]]>

LeetCode Longest Repeating Character Replacement Given a string that consists of only uppercase English letters, you can replace any letter in the string with another letter at most k times. Find the length of a longest substring containing all repeating letters you can get after performing the above operations. Note: Both the string’s length and k will not exceed 10⁴. Example 1:

Input:
s = "ABAB", k = 2
Output:
4
Explanation:
Replace the two 'A's with two 'B's or vice versa.

Example 2:

Input:
s = "AABABBA", k = 1
Output:
4
Explanation:
Replace the one 'A' in the middle with 'B' and form "AABBBBA".
The substring "BBBB" has the longest repeating letters, which is 4.

---

给定一个字符串s，可以把s中最多k个字符换成另一个字符，问这样做之后，最大能得到多长的重复字符的字符串。 比如样例一s=”ABAB”,k=2，把两个A都改为B之后，所有字符都变成了B，长度为4。 本题使用滑动窗口来解。每次我们统计窗口内出现频率最多的字符，那么最好的办法就是把窗口内其他字符全换成最高频的字符，条件就是其他字符的数量要不超过k，这样替换的次数才不会超过k。 在滑动窗口的时候，如果其他字符的数量超过k了，则需要缩减窗口大小，也就是把窗口左端往右滑。 代码如下： [cpp] class Solution { public: int characterReplacement(string s, int k) { int ans = 0, n = s.size(); vector<int> count(26, 0); int start = 0; for (int end = 0; end < n; ++end) { ++count[s[end] – ‘A’]; while (end – start + 1 – *max_element(count.begin(), count.end()) > k) { –count[s[start++] – ‘A’]; } ans = max(ans, end – start + 1); } return ans; } }; [/cpp] 本代码提交AC，用时29MS。渐进复杂度应该是O(n^2)的。 讨论区还有O(n)的方法，但是我看了好久都没理解，为啥max不会减少，为啥返回的直接是s.length()-start。]]>

LeetCode Shortest Unsorted Continuous Subarray Given an integer array, you need to find one continuous subarray that if you only sort this subarray in ascending order, then the whole array will be sorted in ascending order, too. You need to find the shortest such subarray and output its length. Example 1:

Input: [2, 6, 4, 8, 10, 9, 15]
Output: 5
Explanation: You need to sort [6, 4, 8, 10, 9] in ascending order to make the whole array sorted in ascending order.

Note:

1. Then length of the input array is in range [1, 10,000].
2. The input array may contain duplicates, so ascending order here means <=.

---

给定一个数组，问最短对多长的子数组排序之后，整个数组都会是升序的。比如样例对中间的[6,4,8,10,9]这个子数组排序之后，放回到原数组，原数组也是升序排列的。 第一种解法是，直接对数组排序，然后把已排序数组和未排序数组分别从首位对比，遇到第一个不相等的位置就跳出，然后需要排序的子数组长度就是j-i+1了。 代码如下： [cpp] class Solution { public: int findUnsortedSubarray(vector<int>& nums) { vector<int> nums_copy = nums; sort(nums_copy.begin(), nums_copy.end()); int i = 0, j = nums.size() – 1; while (i <= j&&nums[i] == nums_copy[i])++i; while (j >= i&&nums[j] == nums_copy[j])–j; return j – i + 1; } }; [/cpp] 本代码提交AC，用时52MS，时间复杂度是O(nlgn)。 还有一种O(n)的方法，参考这个题解。 基本思想是这样：

1. 从左往右，如果该数已经在最终排序的位置了，那么该数必须小于等于该数右边的最小值
2. 从右往左，如果该数已经在最终排序的位置了，那么该数必须大于等于该数左边的最大值

如果违反1，那么该数右边还有比该数小的数，所以需要把这个更小的数放到该数前面，也就是说该数不在其最终的位置；违反2也是类似的。 所以我们维护两个数组，分别存储从左往右的最大值和从右往左的最小值，然后和原数组比较即可。 代码如下： [cpp] /** * /————\ * nums: [2, 6, 4, 8, 10, 9, 15] * minsf: 2 4 4 8 9 9 15 * <——————– * maxsf: 2 6 6 8 10 10 15 * ——————–> */ class Solution { public: int findUnsortedSubarray(vector<int>& nums) { int n = nums.size(); vector<int> min_so_far(n, 0), max_so_far(n, 0); for (int i = 0, maxsf = INT_MIN; i < n; ++i)max_so_far[i] = maxsf = max(maxsf, nums[i]); for (int i = n – 1, minsf = INT_MAX; i >= 0; –i)min_so_far[i] = minsf = min(minsf, nums[i]); int i = 0, j = n – 1; while (i <= j&&nums[i] <= min_so_far[i])++i; while (j >= i&&nums[j] >= max_so_far[j])–j; return j – i + 1; } }; [/cpp] 本代码提交AC，用时72MS，时间复杂度是O(n)，但是为啥比第一种方法还慢呀。]]>

LeetCode Range Addition II Given an m * n matrix M initialized with all 0‘s and several update operations. Operations are represented by a 2D array, and each operation is represented by an array with two positive integers a and b, which means M[i][j] should be added by one for all 0 <= i < a and 0 <= j < b. You need to count and return the number of maximum integers in the matrix after performing all the operations. Example 1:

Input:
m = 3, n = 3
operations = [[2,2],[3,3]]
Output: 4
Explanation:
Initially, M =
[[0, 0, 0],
 [0, 0, 0],
 [0, 0, 0]]
After performing [2,2], M =
[[1, 1, 0],
 [1, 1, 0],
 [0, 0, 0]]
After performing [3,3], M =
[[2, 2, 1],
 [2, 2, 1],
 [1, 1, 1]]
So the maximum integer in M is 2, and there are four of it in M. So return 4.

Note:

1. The range of m and n is [1,40000].
2. The range of a is [1,m], and the range of b is [1,n].
3. The range of operations size won’t exceed 10,000.

---

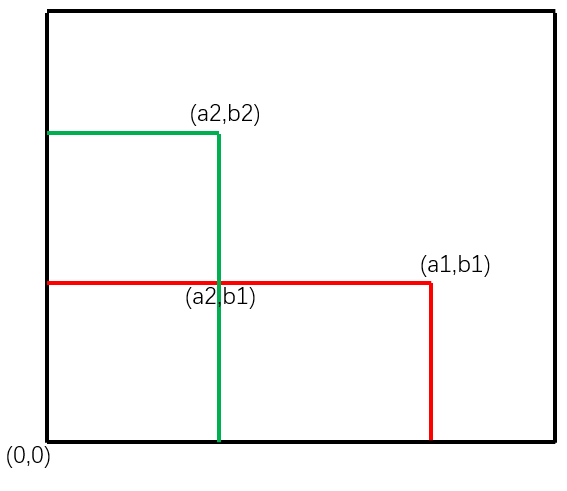给定一个全为0的矩阵M，和一系列的操作，每个操作都是一对(a,b)，表示要对所有i在[0,a)和j在[0,b)的元素M[i][j]，问最终矩阵M中最大元素的个数。 这个题稍微想一下就会发现非常简单。 假设矩阵的左下角坐标为(0,0)，对于某一个操作(a,b)，表示把以(0,0)和(a,b)为对角顶点的子矩阵元素加1。那么(a1,b1)和(a2,b2)两个操作的重叠区域(0,0)-(a2,b1)所在子矩阵的元素就被加了两次，他们的值最大且相同。 所以我们只需要遍历所有操作，分别找到行和列的最小值，则他们和原点围成的子矩阵的元素值最大，且相等。 代码非常简单，如下： [cpp] class Solution { public: int maxCount(int m, int n, vector<vector<int>>& ops) { int minRow = m, minCol = n; for (const auto &op : ops) { minRow = min(minRow, op[0]); minCol = min(minCol, op[1]); } return minRow*minCol; } }; [/cpp] 本代码提交AC，用时6MS。 ]]>

LeetCode Array Nesting A zero-indexed array A consisting of N different integers is given. The array contains all integers in the range [0, N – 1]. Sets S[K] for 0 <= K < N are defined as follows: S[K] = { A[K], A[A[K]], A[A[A[K]]], … }. Sets S[K] are finite for each K and should NOT contain duplicates. Write a function that given an array A consisting of N integers, return the size of the largest set S[K] for this array. Example 1:

Input: A = [5,4,0,3,1,6,2]
Output: 4
Explanation:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.
One of the longest S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}

Note:

1. N is an integer within the range [1, 20,000].
2. The elements of A are all distinct.
3. Each element of array A is an integer within the range [0, N-1].

---

求嵌套集合的最大长度。首先给定原数组A，嵌套集合为S[K] = { A[K], A[A[K]], A[A[A[K]]], … }，就是不断的把值当下标递归的取值，因为数组A中的值的范围也是0~n-1的，所以下标不会超出范围。 暴力方法就是求出每一个S[K]的大小，然后求最大值。但是仔细分析一个样例就会发现，很多S[K]集合是完全一样的，比如第一个样例中，S[0]和S[2]都等于{5，6，2，0}，因为他们构成了一个循环。所以我们可以创建一个visited数组，访问过就置1，只对哪些visited为0的下标开始递归。这样对于第一个样例，其实只需要3次递归就可以了，也就是下标到值的构成的图中环的个数：{5,6,2,0}，{3}，{1,4}。所以总的复杂度其实只有O(n)。 代码如下： [cpp] class Solution { private: int nest(vector<int> &nums, vector<int> &visited, int k) { int ans = 0; while (visited[k] == 0) { visited[k] = 1; ++ans; k = nums[k]; } return ans; } public: int arrayNesting(vector<int>& nums) { int n = nums.size(); vector<int> visited(n, 0); int ans = 0; for (int i = 0; i < nums.size(); ++i) { if (visited[i] == 0) { int cur = nest(nums, visited, i); ans = max(ans, cur); } } return ans; } }; [/cpp] 本代码提交AC，用时39MS。]]>

LeetCode Tag Validator Given a string representing a code snippet, you need to implement a tag validator to parse the code and return whether it is valid. A code snippet is valid if all the following rules hold:

1. The code must be wrapped in a valid closed tag. Otherwise, the code is invalid.
2. A closed tag (not necessarily valid) has exactly the following format : <TAG_NAME>TAG_CONTENT</TAG_NAME>. Among them, <TAG_NAME> is the start tag, and </TAG_NAME> is the end tag. The TAG_NAME in start and end tags should be the same. A closed tag is valid if and only if the TAG_NAME and TAG_CONTENT are valid.
3. A valid TAG_NAME only contain upper-case letters, and has length in range [1,9]. Otherwise, the TAG_NAME is invalid.
4. A valid TAG_CONTENT may contain other valid closed tags, cdata and any characters (see note1) EXCEPT unmatched <, unmatched start and end tag, and unmatched or closed tags with invalid TAG_NAME. Otherwise, the TAG_CONTENT is invalid.
5. A start tag is unmatched if no end tag exists with the same TAG_NAME, and vice versa. However, you also need to consider the issue of unbalanced when tags are nested.
6. A < is unmatched if you cannot find a subsequent >. And when you find a < or </, all the subsequent characters until the next > should be parsed as TAG_NAME (not necessarily valid).
7. The cdata has the following format : <![CDATA[CDATA_CONTENT]]>. The range of CDATA_CONTENT is defined as the characters between <![CDATA[ and the first subsequent]]>.
8. CDATA_CONTENT may contain any characters. The function of cdata is to forbid the validator to parse CDATA_CONTENT, so even it has some characters that can be parsed as tag (no matter valid or invalid), you should treat it as regular characters.

Valid Code Examples:

Input: "<DIV>This is the first line <![CDATA[<div>]]></DIV>"
Output: True
Explanation:
The code is wrapped in a closed tag : <DIV> and </DIV>.
The TAG_NAME is valid, the TAG_CONTENT consists of some characters and cdata.
Although CDATA_CONTENT has unmatched start tag with invalid TAG_NAME, it should be considered as plain text, not parsed as tag.
So TAG_CONTENT is valid, and then the code is valid. Thus return true.
Input: "<DIV>>>  ![cdata[]] <![CDATA[<div>]>]]>]]>>]</DIV>"
Output: True
Explanation:
We first separate the code into : start_tag|tag_content|end_tag.
start_tag -> "<DIV>"
end_tag -> "</DIV>"
tag_content could also be separated into : text1|cdata|text2.
text1 -> ">>  ![cdata[]] "
cdata -> "<![CDATA[<div>]>]]>", where the CDATA_CONTENT is "<div>]>"
text2 -> "]]>>]"
The reason why start_tag is NOT "<DIV>>>" is because of the rule 6.
The reason why cdata is NOT "<![CDATA[<div>]>]]>]]>" is because of the rule 7.

Invalid Code Examples:

Input: "<A>  <B> </A>   </B>"
Output: False
Explanation: Unbalanced. If "<A>" is closed, then "<B>" must be unmatched, and vice versa.
Input: "<DIV>  div tag is not closed  <DIV>"
Output: False
Input: "<DIV>  unmatched <  </DIV>"
Output: False
Input: "<DIV> closed tags with invalid tag name  <b>123</b> </DIV>"
Output: False
Input: "<DIV> unmatched tags with invalid tag name  </1234567890> and <CDATA[[]]>  </DIV>"
Output: False
Input: "<DIV>  unmatched start tag <B>  and unmatched end tag </C>  </DIV>"
Output: False

Note:

1. For simplicity, you could assume the input code (including the any characters mentioned above) only contain letters, digits, '<','>','/','!','[',']' and ' '.

---

本题需要写一个检查简单html源代码标签是否匹配的程序。规则有很多，8条，比如tag长度必须在[1,9]，且必须是大写字母，还有<![CDATA[CDATA_CONTENT]]>这个东西，经常会在html源代码中看见。 这题在比赛的时候没想清楚，思路比较乱。比赛结束之后，看了讨论区的解答，感觉思路好清晰，借鉴过来。 需要检查的主要有两个部分，一是Tag标签匹配，二是cdata。对于cdata，只要找到，则可以过滤掉<![CDATA[和]]>之间的所有内容。对于Tag标签匹配，类似括号匹配，可以用栈来实现。 但是因为Tag和cdata的开头都有<，我们匹配的时候， 应该从特殊到一般，即首先考虑是<![CDATA，其次考虑是</，然后考虑是<，最后就是一般性的字符了。 当遇到<![CDATA时，找到对应的]]>，下标快速跳到]]>的下一位。 当遇到</时，说明遇到了一个结束Tag，此时判断Tag是否合法，如果合法，从栈中弹出开始Tag，判断开始Tag和结束Tag是否匹配。 当遇到<时，说明遇到了一个开始Tag，判断Tag是否合法，如果合法，则压栈。 如果是一般性的字符，下标直接向前进。 需要注意的是，如果i!=0但是栈为空，说明当前的字符不在某个Tag标签内，比如这个样例：<![CDATA[wahaha]]]><![CDATA[]> wahaha]]>，一上来就是cdata，这是不合法的，因为所有内容都应该在标签对内。 完整代码如下： [cpp] class Solution { private: bool checkTag(const string &tag) { if (tag.size() < 1 || tag.size() > 9)return false; for (const auto &c : tag) { if (!isupper(c))return false; } return true; } public: bool isValid(string code) { stack<string> stk; int i = 0; while (i < code.size()) { if (i > 0 && stk.empty())return false; if (code.substr(i, 9) == "<![CDATA[") { int end = code.find("]]>", i); if (end == string::npos)return false; i = end + 3; } else if (code.substr(i, 2) == "</") { int end = code.find(‘>’, i); if (end == string::npos)return false; string tag = code.substr(i + 2, end – i – 2); if (!checkTag(tag))return false; if (stk.empty() || stk.top() != tag)return false; else stk.pop(); i = end + 1; } else if (code[i] == ‘<‘) { int end = code.find(‘>’, i); if (end == string::npos)return false; string tag = code.substr(i + 1, end – i – 1); if (!checkTag(tag))return false; stk.push(tag); i = end + 1; } else { ++i; } } return stk.empty(); } }; [/cpp] 本代码提交AC，用时12MS。]]>