1514. Path with Maximum Probability
You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].
Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.
If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.
Example 1:
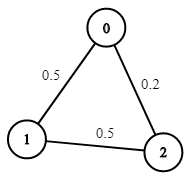
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2 Output: 0.25000 Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.
Example 2:
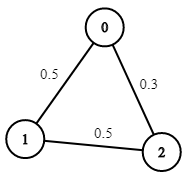
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2 Output: 0.30000
Example 3:
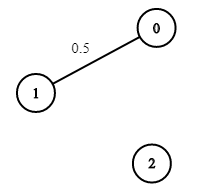
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2 Output: 0.00000 Explanation: There is no path between 0 and 2.
Constraints:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1- There is at most one edge between every two nodes.
给定一个无向图,边表示概率,问从start到end的最大概率是多少。
借此题复习一下若干最短路径算法吧。
首先朴素的DFS,代码如下:
class Solution {
private:
void DFS(const vector<vector<double>> &graph, vector<int> &visited, int start, int end, double curprob, double &maxprob) {
if (start == end) {
maxprob = max(maxprob, curprob);
return;
}
int n = graph.size();
for (int i = 0; i < n; ++i) {
if (visited[i] == 0 && graph[start][i] >= 0) {
visited[i] = 1;
DFS(graph, visited, i, end, curprob*graph[start][i], maxprob);
visited[i] = 0;
}
}
}
public:
double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
vector<vector<double>> graph(n, vector<double>(n, -1.0));
for (int i = 0; i < edges.size(); ++i) {
graph[edges[i][0]][edges[i][1]] = succProb[i];
graph[edges[i][1]][edges[i][0]] = succProb[i];
}
vector<int> visited(n, 0);
visited[start] = 1;
double maxprob = 0;
DFS(graph, visited, start, end, 1, maxprob);
return maxprob;
}
};本代码提交TLE。
其次, 朴素的迪杰斯特拉算法。迪杰斯特拉算法思路很简单,维护两个集合,一个集合S是已经找到最短路径的,另一个集合U是还未找到最短路径的。每次,从U选一个距离最小的节点u,这个节点已经是最短路径了,加入到S中。然后更新与u相连的其他节点的最短路径。如此循环往复。代码如下:
// 朴素迪杰斯特拉
class Solution {
public:
double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
vector<unordered_map<int, double>> graph(n, unordered_map<int, double>());
for (int i = 0; i < edges.size(); ++i) {
graph[edges[i][0]][edges[i][1]] = succProb[i];
graph[edges[i][1]][edges[i][0]] = succProb[i];
}
vector<int> visited(n, 0);
visited[start] = 1;
vector<double> ans(n, 0);
for (int i = 0; i < n; ++i) {
ans[i] = graph[start][i];
}
while (true) {
int maxid = -1;
double maxprob = 0;
for (int i = 0; i < n; ++i) {
if (visited[i] == 0 && ans[i] > maxprob) {
maxid = i;
maxprob = ans[i];
}
}
if (maxid == -1 || maxid == end)break; // 遇到end提前结束
visited[maxid] = 1;
for (unordered_map<int, double>::iterator it = graph[maxid].begin(); it != graph[maxid].end(); ++it) {
int next = it->first;
double prob = it->second;
if (visited[next] == 0 && (maxprob*prob > ans[next])) {
ans[next] = maxprob * prob;
}
}
}
return ans[end];
}
};很遗憾,上述代码在最后一个样例上TLE了。
优化版本的迪杰斯特拉算法。朴素迪杰斯特拉算法最耗时的是while循环内的两个for循环,第二个for循环是对找到的u节点的边进行循环,这个无法再优化,主要优化第一个for循环,即在U集合中找距离最短的u节点的过程。这里可以用优先队列来存储U中的所有节点。但是需要注意的是去重,比如题目中的第一个图,对于节点2,节点0弹出pq时,会访问节点2并把节点2加入到pq中;当节点1弹出pq时,又会访问节点2并把节点2加入到pq中,此时pq中出现了两个节点2,只不过prob不一样。所以pq弹出时可能会出现相同的节点,不过由于pq的性质,同样是2,先弹出来的肯定是概率最大的路径(最短路径),所以每次pq弹出时,更新visited数组,后续如果弹出的节点已经visited了,则不需要做第二个for循环了,直接continue。比如题目中的第一个图,0访问2时,压pq的是(id=2,prob=0.2);1访问2时,压pq的是(id=2,prob=0.25)。所以(id=2,prob=0.25)先于(id=2,prob=0.2)弹出,并设置visited[2]=1。当(id=2,prob=0.2)弹出时,visited[2]已经==1了,此时continue。
// 优化的迪杰斯特拉
struct P {
int id_;
double prob_;
P(int id, double prob) :id_(id), prob_(prob) {};
// priority_queue默认是最大堆,即小于就是小于
bool operator<(const P& p) const {
return this->prob_ < p.prob_;
}
};
class Solution {
public:
double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
vector<unordered_map<int, double>> graph(n, unordered_map<int, double>());
for (int i = 0; i < edges.size(); ++i) {
graph[edges[i][0]][edges[i][1]] = succProb[i];
graph[edges[i][1]][edges[i][0]] = succProb[i];
}
vector<int> visited(n, 0);
vector<double> ans(n, 0);
ans[start] = 1;
priority_queue<P> pq;
pq.push(P(start, 1));
while (!pq.empty()) {
P cur = pq.top();
pq.pop();
if (cur.id_ == end)break; // 提前结束
if (visited[cur.id_] == 1)continue;
visited[cur.id_] = 1;
for (unordered_map<int, double>::iterator it = graph[cur.id_].begin(); it != graph[cur.id_].end(); ++it) {
int next = it->first;
double prob = it->second;
if (cur.prob_*prob > ans[next]) {
ans[next] = cur.prob_*prob;
pq.push(P(next, ans[next]));
}
}
}
return ans[end];
}
};本代码提交AC,用时428MS。
SPFA算法。SPFA算法的思想可以参考之前的一道题: http://code.bitjoy.net/2014/12/28/hihocoder-1093/ 。
简单来说,SPFA就是带剪枝的BFS。它和迪杰斯特拉算法非常像,迪杰斯特拉算法是每次找U中距离最小的一个节点u,此时u的最短距离已经确定了,后续不会再更新了。因为迪杰斯特拉算法每次加入S的节点都是最优的,所以必须要线性(朴素迪杰斯特拉算法)或者用优先队列的方法从U中找到最小距离节点u。而SPFA算法就更简单一点,该算法不要求每次找到最优的节点u,因为SPFA是渐进逼近最优解的过程,它不需要线性查找,也不需要优先队列,它只需要一个简单的队列即可,每次把可以更新的节点u加入到队列中,然后BFS更新与u相连的其他节点。之前更新过的节点,后续还有可能更新。代码如下:
// SPFA
class Solution {
public:
double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
vector<unordered_map<int, double>> graph(n, unordered_map<int, double>());
for (int i = 0; i < edges.size(); ++i) {
graph[edges[i][0]][edges[i][1]] = succProb[i];
graph[edges[i][1]][edges[i][0]] = succProb[i];
}
vector<int> visited(n, 0);
visited[start] = 1;
vector<double> ans(n, 0);
ans[start] = 1;
queue<int> q;
q.push(start);
while (!q.empty()) {
int cur = q.front();
q.pop();
visited[cur] = 0;
for (unordered_map<int, double>::iterator it = graph[cur].begin(); it != graph[cur].end(); ++it) {
int next = it->first;
double prob = it->second;
if (ans[cur] * prob > ans[next]) {
ans[next] = ans[cur] * prob;
if (visited[next] == 0) {
visited[next] = 1;
q.push(next);
}
}
}
}
return ans[end];
}
};本代码提交AC,用时392MS。