5474. Number of Good Leaf Nodes Pairs

Given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.

Return the number of good leaf node pairs in the tree.

Example 1:

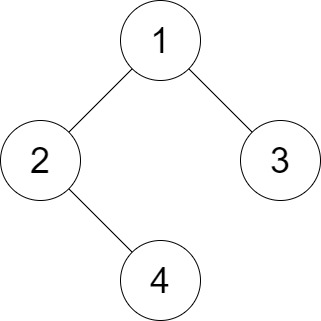
Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.

Example 2:

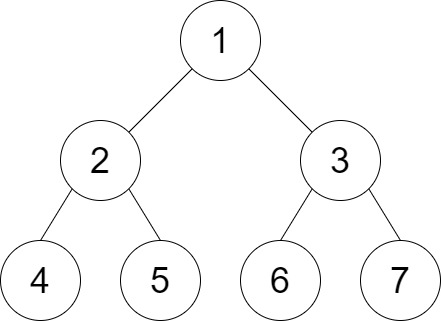
Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.

Example 3:

Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
Output: 1
Explanation: The only good pair is [2,5].

Example 4:

Input: root = [100], distance = 1
Output: 0

Example 5:

Input: root = [1,1,1], distance = 2
Output: 1

Constraints:

• The number of nodes in the tree is in the range [1, 2^10].
• Each node’s value is between [1, 100].
• 1 <= distance <= 10

---

这一题第一眼看上去还是有难度的，后来观察数据量，发现总节点数才1024，则叶子节点数会更少，所以首先尝试了暴力方法。

暴力方法分为两个阶段，第一阶段是找到所有的叶子节点，第二阶段是求任意两个叶子节点的最短距离。

第一阶段在递归查找所有叶子节点时，保留了从根到该叶子的路径，以便后续求任意两个叶子的距离。第二阶段求距离时，思路比较简单，比如第一个样例，节点4的路径是1-2-4，节点3的路径是1-3，则两条路径都从根节点开始，看看两者的最长的公共前缀，直到找到它们的最后一个公共节点，相当于它们的最近公共祖先，然后假设最近公共祖先为两个叶子的子树的根节点，算两个叶子的高度，高度相加就是它们的最短距离。完整代码如下：

class Solution {
private:
	void CollectLeaves(TreeNode *root, unordered_map<TreeNode*, vector<TreeNode*>> &all_paths, vector<TreeNode*> &one_path) {
		if (root == NULL)return;
		one_path.push_back(root);
		if (root->left == NULL && root->right == NULL) {
			all_paths[root] = one_path;
		}
		else {
			CollectLeaves(root->left, all_paths, one_path);
			CollectLeaves(root->right, all_paths, one_path);
		}
		one_path.pop_back();
	}
	int CalDist(vector<TreeNode*> &path1, vector<TreeNode*> &path2) {
		int m = path1.size(), n = path2.size();
		int i = 0;
		while (i < m&&i < n) {
			if (path1[i] != path2[i])break;
			++i;
		}
		return (m - i) + (n - i);
	}

public:
	int countPairs(TreeNode* root, int distance) {
		unordered_map<TreeNode*, vector<TreeNode*>> all_paths;
		vector<TreeNode*> one_path;
		CollectLeaves(root, all_paths, one_path);
		vector<TreeNode*> leaves;
		for (unordered_map<TreeNode*, vector<TreeNode*>>::iterator it = all_paths.begin(); it != all_paths.end(); ++it) {
			leaves.push_back(it->first);
		}

		int ans = 0;
		for (int i = 0; i < leaves.size(); ++i) {
			for (int j = i + 1; j < leaves.size(); ++j) {
				int d = CalDist(all_paths[leaves[i]], all_paths[leaves[j]]);
				if (d <= distance)++ans;
			}
		}

		return ans;
	}
};

本代码提交AC。