5383. Number of Ways to Paint N × 3 Grid
You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colours: Red, Yellow or Green while making sure that no two adjacent cells have the same colour (i.e no two cells that share vertical or horizontal sides have the same colour).
You are given n the number of rows of the grid.
Return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 10^9 + 7.
Example 1:
Input: n = 1 Output: 12 Explanation: There are 12 possible way to paint the grid as shown:
Example 2:
Input: n = 2 Output: 54
Example 3:
Input: n = 3 Output: 246
Example 4:
Input: n = 7 Output: 106494
Example 5:
Input: n = 5000 Output: 30228214
Constraints:
n == grid.lengthgrid[i].length == 31 <= n <= 5000
给定3种颜色,要求涂满N*3的网格,且相邻网格的颜色不能一样,问有多少种涂法。
首先,如果只有一行的话。如果涂3种颜色,则因为3种颜色各不相同,所以有3种排列的方法,共3!=6种。如果涂2种颜色,则相同的颜色涂两边,不同的颜色涂中间,首先从3种颜色中选2种,为$C_3^2$,2种颜色决定哪个放中间有2种方法,所以也有6种涂法。
对于涂3种颜色的一行,其下一行可以涂2种颜色,有2种涂法;也可以涂3种颜色,也有2种涂法。
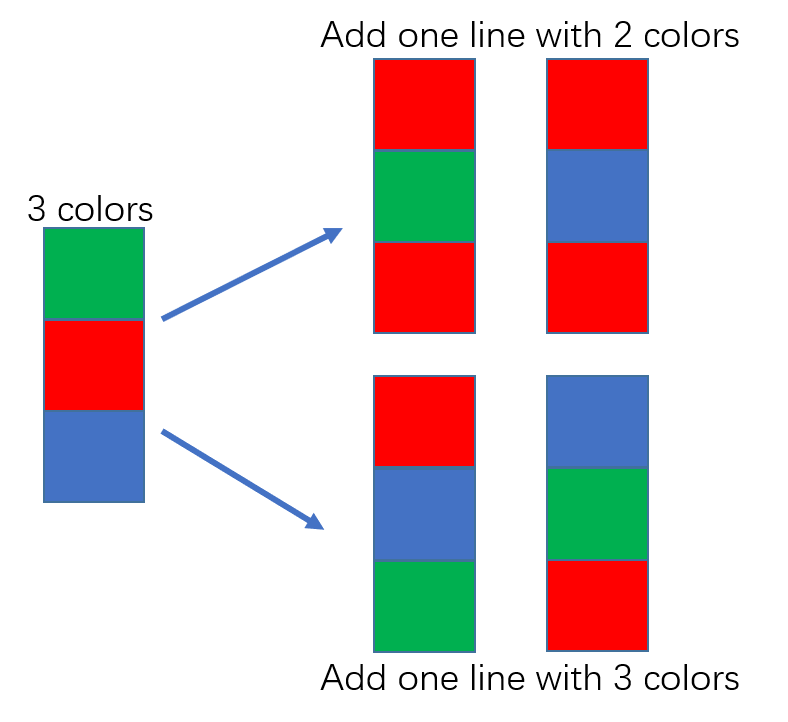
对于涂2种颜色的一行,其下一行可以涂2种颜色,有3种涂法;也可以涂3种颜色,有2种涂法。
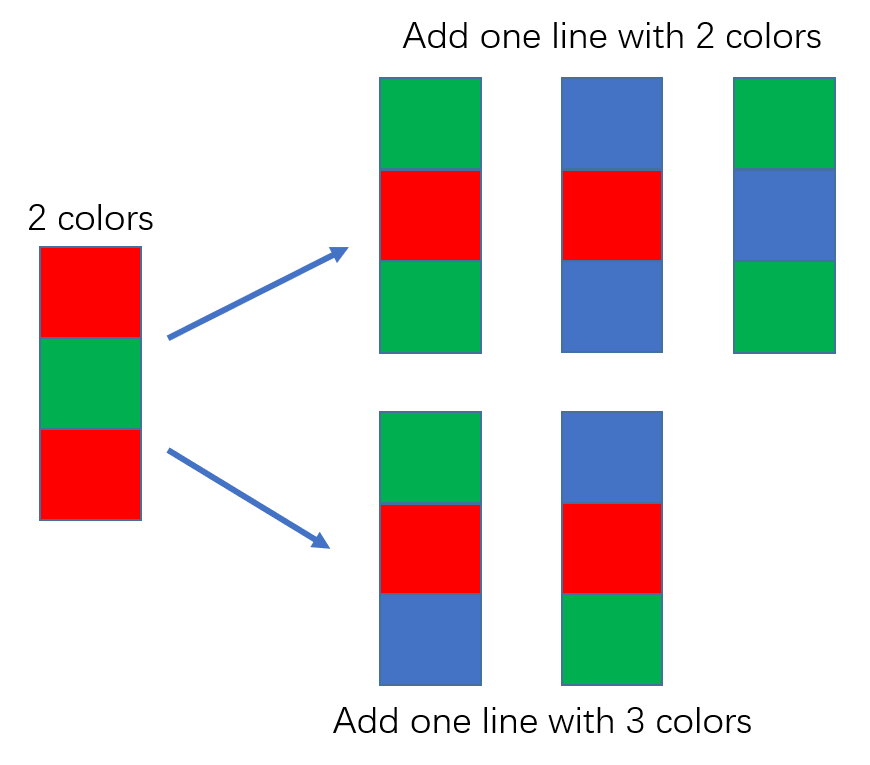
综合上面两种情况,下一行是2种颜色的情况=上一行是3种颜色*2+上一行是2种颜色*3,类似的,下一行是3种颜色的情况=上一行是3种颜色*2+上一行是2种颜色*2。根据递推公式,最终的情况数是两者相加,代码如下:
class Solution {
public:
int numOfWays(int n) {
if (n == 1)return 12;
long long pre_two_colors = 6, pre_three_colors = 6;
long long mod = 1e9 + 7;
for (int i = 2; i <= n; ++i) {
long long next_two_colors = 3 * pre_two_colors + 2 * pre_three_colors;
long long next_three_colors = 2 * pre_two_colors + 2 * pre_three_colors;
pre_two_colors = next_two_colors % mod;
pre_three_colors = next_three_colors % mod;
}
return (pre_two_colors + pre_three_colors) % mod;
}
};本代码提交AC,用时0MS。
参考: