111. Minimum Depth of Binary Tree

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

return its minimum depth = 2.

---

求一棵二叉树的最小深度，类似于LeetCode Maximum Depth of Binary Tree求最大深度，但是稍微难一点。 请注意，不能直接把求最大深度的大于号改为小于号：

class Solution {
public:
    int dfs(TreeNode* root, int nDepth)
    {
        if (root == NULL)
            return nDepth;
        int left = dfs(root->left, nDepth + 1);
        int right = dfs(root->right, nDepth + 1);
        return left < right ? left : right;
    }
    int minDepth(TreeNode* root) { return dfs(root, 0); }
};

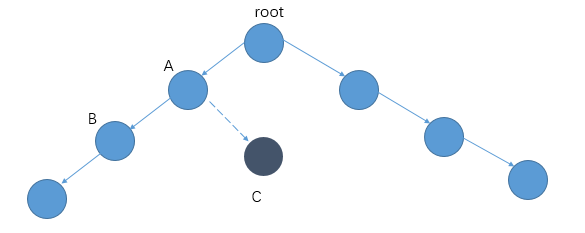
因为如上图所示，当走到A点时，没有右孩子，导致int right = dfs(root->right, nDepth + 1);会得到A点的高度2，比左孩子的高度低，即最小高度为2了。但是最小高度显然是4。所以需要稍加修改，使得如果某个孩子为空时，不在该孩子深搜了，只有当两个孩子都为空时（即是叶子节点时），才得到一个合法的深度，去和其他深度做比较。

深度搜索的完整代码如下：

class Solution {
public:
    int dfs(TreeNode* root, int nDepth)
    {
        if (root == NULL)
            return nDepth;
        if (root->left == NULL && root->right == NULL)
            return nDepth + 1;
        int left = root->left == NULL ? INT_MAX : dfs(root->left, nDepth + 1);
        int right = root->right == NULL ? INT_MAX : dfs(root->right, nDepth + 1);
        return left < right ? left : right;
    }
    int minDepth(TreeNode* root) { return dfs(root, 0); }
};

本代码提交AC，用时9MS。
但是DFS必须走到所有叶子节点才能得到最小深度，而如果采用广度优先搜索BFS时，遇到的第一个叶子节点的深度就是最小深度了，就可以返回了。所以理论上，BFS的性能会更优。
BFS的完整代码如下：

struct NewTreeNode {
    TreeNode* tn;
    int depth;
};
class Solution {
public:
    int bfs(TreeNode* root)
    {
        queue<NewTreeNode*> qTree;
        NewTreeNode* ntn = new NewTreeNode;
        ntn->tn = root;
        ntn->depth = 0;
        qTree.push(ntn);
        NewTreeNode* top = new NewTreeNode;
        while (!qTree.empty()) {
            top = qTree.front();
            qTree.pop();
            if (top->tn == NULL)
                return top->depth;
            if (top->tn->left == NULL && top->tn->right == NULL)
                return top->depth + 1;
            if (top->tn->left != NULL) {
                NewTreeNode* tmp = new NewTreeNode;
                tmp->tn = top->tn->left;
                tmp->depth = top->depth + 1;
                qTree.push(tmp);
            }
            if (top->tn->right != NULL) {
                NewTreeNode* tmp = new NewTreeNode;
                tmp->tn = top->tn->right;
                tmp->depth = top->depth + 1;
                qTree.push(tmp);
            }
        }
        return -1;
    }
    int minDepth(TreeNode* root) { return bfs(root); }
};

本代码提交AC，用时也是9MS。
我看Leetcode上有很多关于树的题，为了方便测试，自己写了一个由数组构造树结构的函数，如下：

#include <vector>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x)
        : val(x)
        , left(NULL)
        , right(NULL)
    {
    }
};
TreeNode* genTree(vector<int>& vi, int id)
{
    if (vi.size() == 0)
        return NULL;
    TreeNode* root = new TreeNode(vi[id]);
    if (2 * id + 1 < vi.size() && vi[2 * id + 1] != -1) {
        root->left = genTree(vi, 2 * id + 1);
    }
    if (2 * id + 2 < vi.size() && vi[2 * id + 2] != -1) {
        root->right = genTree(vi, 2 * id + 2);
    }
    return root;
}
int main()
{
    vector<int> vTree = { 1, 2, 3, 4, 5 };
    TreeNode* root = genTree(vTree, 0);
    return 0;
}

使用时只要传入数组和0，返回的就是一个建好的树。用数组存树，一般第i号节点的左右孩子下标分别为2i+1和2i+2。存好之后恰好是一棵树的层次遍历结果。
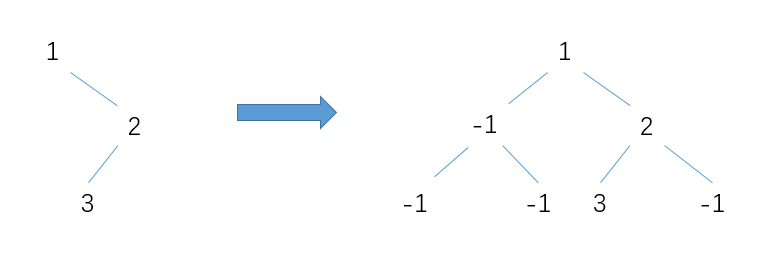
如果要构建的不是一棵完全树，比如下面的左图，则先需要转换为完全图，也就是用-1代替一个不存在的节点，此时传入的数组应该是[1,-1,2,-1,-1,3,-1]，genTree函数遇到-1会自动跳过不创建节点。当然如果你的树中本来就有-1这个值，也可以把-1换成其他数。

二刷。BFS的代码还可以写得更简洁漂亮一些，类似于层次遍历，遍历到某一层有叶子节点时，层数就是最小深度，代码如下：

class Solution {
public:
    int minDepth(TreeNode* root)
    {
        if (root == NULL)
            return 0;
        int depth = 0;
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            ++depth;
            int n = q.size();
            while (n--) {
                TreeNode* cur = q.front();
                q.pop();
                if (cur->left == NULL && cur->right == NULL)
                    return depth;
                if (cur->left != NULL)
                    q.push(cur->left);
                if (cur->right != NULL)
                    q.push(cur->right);
            }
        }
        return depth;
    }
};

本代码提交AC，用时9MS。
DFS的代码也可以写得更漂亮一些：

class Solution {
public:
    int minDepth(TreeNode* root)
    {
        if (root == NULL)
            return 0;
        if (root->left == NULL)
            return minDepth(root->right) + 1;
        if (root->right == NULL)
            return minDepth(root->left) + 1;
        return min(minDepth(root->left), minDepth(root->right)) + 1;
    }
};

本代码提交AC，用时13MS，比BFS慢。