1377. Frog Position After T Seconds
Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from the vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them with the same probability, otherwise, when the frog can not jump to any unvisited vertex it jumps forever on the same vertex.
The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting directly the vertices fromi and toi.
Return the probability that after t seconds the frog is on the vertex target.
Example 1:
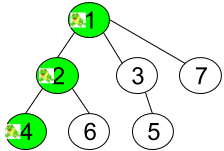
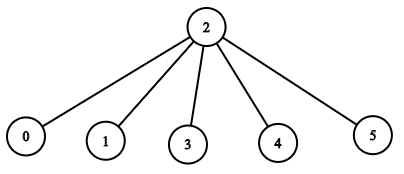
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4 Output: 0.16666666666666666 Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666.
Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7 Output: 0.3333333333333333 Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1.
Example 3:
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6 Output: 0.16666666666666666
Constraints:
1 <= n <= 100edges.length == n-1edges[i].length == 21 <= edges[i][0], edges[i][1] <= n1 <= t <= 501 <= target <= n- Answers within
10^-5of the actual value will be accepted as correct.
这题其实不是很hard。
给定一个无向树,节点编号是1~n。有一个青蛙开始在1号节点,每秒钟它会随机跳到与其相邻的未被访问的过的节点中,注意不能走回头路,访问过的节点不能再访问了。如果它周围的节点都被访问了,则它就在原地打转。问经过t秒,它跳到指定节点的概率是多少。
解法。从1号节点开始BFS,每到一个节点时,记录当前走过的时间以及走到当前节点的概率。计算概率也很简单,维护一个visited数组,看看有多少个未被访问的邻居child,则路径概率要乘上(1/child)。
还需要注意的是,如果走到目标节点的时间大于给定时间,则走不到目标节点;如果走的时间小于给定时间,则要看看目标节点还有没有未被访问的节点,如果没有的话,青蛙在目标节点原地打转,否则青蛙就跳走了不会再回来了。
完整代码如下:
struct Point {
int id, time;
double prob;
Point(int i, int t, double p) :id(i), time(t), prob(p) {};
};
class Solution {
public:
double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));
for (int i = 0; i < edges.size(); ++i) {
graph[edges[i][0]][edges[i][1]] = 1;
graph[edges[i][1]][edges[i][0]] = 1;
}
vector<int> visited(n + 1, 0);
double prob = 1.0;
int time = 0;
queue<Point> q;
q.push(Point(1, 0, 1.0));
while (true) {
Point cur = q.front();
q.pop();
if (cur.id == target) {
prob = cur.prob;
time = cur.time;
break;
}
visited[cur.id] = 1;
int child = 0;
for (int i = 1; i <= n; ++i) {
if (visited[i] == 0 && graph[cur.id][i] == 1) {
++child;
}
}
for (int i = 1; i <= n; ++i) {
if (visited[i] == 0 && graph[cur.id][i] == 1) {
Point next(i, cur.time + 1, cur.prob / child);
q.push(next);
}
}
}
if (t < time)return 0;
else if (t == time)return prob;
else {
int child = 0;
for (int i = 1; i <= n; ++i) {
if (visited[i] == 0 && graph[target][i] == 1) {
++child;
}
}
if (child == 0)return prob;
else return 0;
}
}
};本代码提交AC,用时40MS。