5418. Pseudo-Palindromic Paths in a Binary Tree
Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.
Return the number of pseudo-palindromic paths going from the root node to leaf nodes.
Example 1:
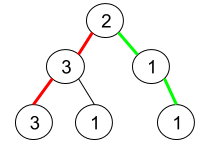
Input: root = [2,3,1,3,1,null,1] Output: 2 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 2:
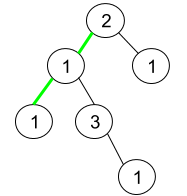
Input: root = [2,1,1,1,3,null,null,null,null,null,1] Output: 1 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 3:
Input: root = [9] Output: 1
Constraints:
- The given binary tree will have between
1and10^5nodes. - Node values are digits from
1to9.
给定一棵二叉树,问树中从根到叶子的路径构成的一个数组,能调整成回文数组串的个数。
简单题,直接DFS,记录每条路径中包含1~9的个数,如果该数组中包含的奇数的个数不超过1个,则能调整成回文串,否则不能。
回文串有两种形式,一种是123321,即串中每个数字都对称出现偶数次,另一种是1234321,中间的4只出现1次,其他数字都出现偶数次。
完整代码如下:
class Solution {
private:
void DFS(TreeNode* root, vector<int> &hash, int &ans) {
if (root == NULL)return;
++hash[root->val];
if (root->left == NULL && root->right == NULL) {
int odd = 0;
for (int i = 1; i <= 9; ++i) {
if (hash[i] % 2 == 1) {
++odd;
if (odd > 1) {
break;
}
}
}
if (odd <= 1) {
++ans;
}
--hash[root->val];
return;
}
DFS(root->left, hash, ans);
DFS(root->right, hash, ans);
--hash[root->val];
}
public:
int pseudoPalindromicPaths(TreeNode* root) {
vector<int> hash(10, 0);
int ans = 0;
DFS(root, hash, ans);
return ans;
}
};
本代码提交AC。